
Theorem 5.10 (K,)=n-1 一 定是两 证明: 个吗? 1, 显然,(Kn)≤n-1 2,令X是某个minimum边割集,将G分割为两个连通分量G1和G2 不失一般性,G1中含有k个点,G2中有-k个点 |XI=k*(n-k)∥G是完全图 k-1≥0,n-k-1≥0,所以: (k-1)(n-k-1)=k(n-k)-(n-1)≥0 k(n-k)≥n-1 G G2 λ(Kn)=lX|=k(n-k)≥n-1 3,λ(Kn)=n-1
Theorem 5.10 𝜆 𝐾𝑛 = 𝑛 − 1 证明: 1,显然,𝜆 𝐾𝑛 ≤ 𝑛 − 1 2,令X是某个minimum边割集,将G分割为两个连通分量G1和G2 不失一般性,G1中含有k个点,G2中有n-k个点 |𝑋| = 𝑘 ∗ (𝑛 − 𝑘) 𝑘 − 1 ≥ 0,𝑛 − 𝑘 − 1 ≥ 0, 所以: 𝑘 − 1 𝑛 − 𝑘 − 1 = 𝑘 𝑛 − 𝑘 − 𝑛 − 1 ≥ 0 𝑘 𝑛 − 𝑘 ≥ 𝑛 − 1 𝜆 𝐾𝑛 = 𝑋 = 𝑘(𝑛 − 𝑘) ≥ 𝑛 − 1 3, 𝜆 𝐾𝑛 = 𝑛 − 1 G1 G2 一定是两 个吗? // G 是完全图
Vhitney.定理 Theorem 5.11 For every graph G, K(G)≤λ(G)≤6(G) 证明:1,平凡图和完全图是符合定理要求的:0,或者n一1 2,对非完全图,显然,λ(G)≤6(G)≤n-2 3,对非完全图,令X是某个最小边割集,X=1(G)≤n-2。X集合将G分割为两个连通分量G1和G2 观察K(G)和(G) G1 G2
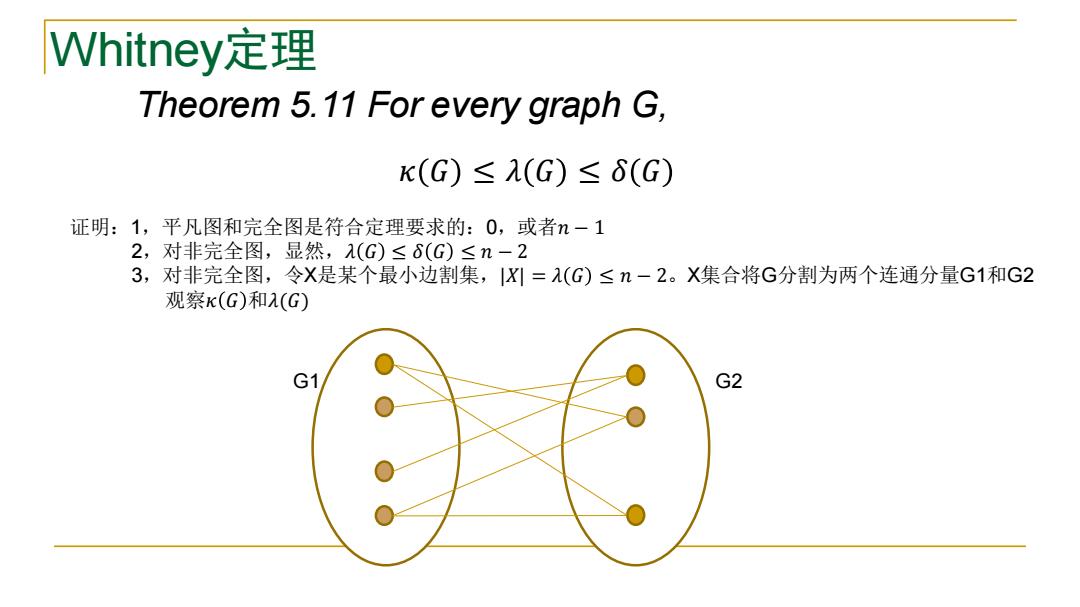
Whitney定理 Theorem 5.11 For every graph G, 证明:1,平凡图和完全图是符合定理要求的:0,或者𝑛 − 1 2,对非完全图,显然,𝜆 𝐺 ≤ 𝛿 𝐺 ≤ 𝑛 − 2 3,对非完全图,令X是某个最小边割集,|𝑋| = 𝜆 𝐺 ≤ 𝑛 − 2。X集合将G分割为两个连通分量G1和G2 观察𝜅 𝐺 和𝜆(𝐺) G1 G2 𝜅 𝐺 ≤ 𝜆 𝐺 ≤ 𝛿 𝐺