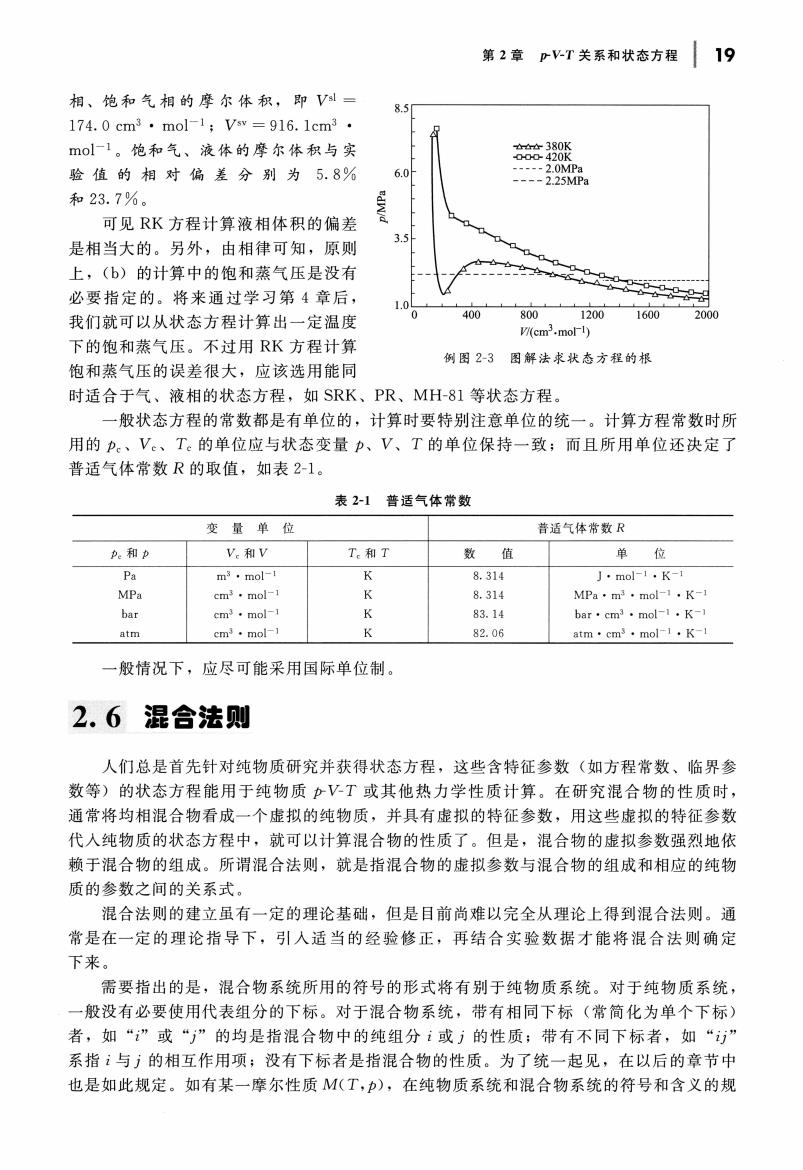
第2章PT关系和状态方程19 相、饱和气相的摩尔体积,即V一 8.3 174.0cm3·mol-1;V=916.1cm3 mol1。饱和气、液体的摩尔体积与实 验值的相对偏差分别为5.8% 和23.7%。 可见RK方程计算液相体积的偏差 是相当大的。另外,由相律可知,原则 上,(b)的计算中的饱和蒸气压是没有 必要指定的。将来通过学习第4章后, ,0 我们就可以从状态方程计算出一定温度 400 1200 下的饱和蒸气压。不过用RK方程计算 例图2-3图解法求状态方程的根 饱和蒸气压的误差很大,应该选用能同 时适合于气、液相的状态方程,如SRK、PR、MH-81等状态方程。 一般状态方程的常数都是有单位的,计算时要特别注意单位的统一。计算方程常数时所 用的p。、V。、T。的单位应与状态变量力、V、T的单位保持一致:而且所用单位还决定了 普适气体常数R的取值,如表2-1。 表2-1普适气体常数 变量单位 普适气体常数R A和P .和V T和T 数值 单位 m·mo 8.314 J·molF·K 8.31 MPa·mmol-K- bar·cm3·m atm cmmol 82.0 atm·cm·moK 一般情况下,应尽可能采用国际单位制 2.6混合法则 人们总是首先针对纯物质研究并获得状态方程,这些含特征参数(如方程常数、临界参 数等)的状态方程能用于纯物质pVT或其他热力学性质计算。在研究混合物的性质时, 通常将均相混合物看成一个虚拟的纯物质,并具有虚拟的特征参数,用这些虚拟的特征参数 代人纯物质的状态方程中,就可以计算混合物的性质了。但是,混合物的虚拟参数强烈地依 赖于混合物的组成。所谓混合法则,就是指混合物的虚拟参数与混合物的组成和相应的纯物 质的参数之间的关系式。 混合法则的建立虽有一定的理论基础,但是日前尚难以完全从理论上得到混合法则。通 常是在一定的理论指导下,引人适当的经验修正,再结合实验数据才能将混合法则确定 下来。 需要指出的是,混合物系统所用的符号的形式将有别于纯物质系统。对于纯物质系统, 般没有必要使用代表组分的下标。对于混合物系统,带有相同下标(常简化为单个下标) 者,如“”或“”的均是指混合物中的纯组分i或j的性质:带有不同下标者,如“” 系指:与方的相互作用项;没有下标者是指混合物的性质。为了统一起见,在以后的章节中 也是如此规定。如有某一摩尔性质M(T,),在纯物质系统和混合物系统的符号和含义的规
川关系和状态 19 相、饱和气相的摩尔体积,即 174.0 cm3 • mo]- l; Vsv = 916. 1cm3 • 8.5 mo] 饱和气、液体的摩尔体和、与实 验值的相对偏差分别为 5.8 6.0 23.7 0 ~ 可见 RK 方程计算液相体积的偏 是相当大的 另外,由相律可知,原则 上,他)的计算中的饱和蒸气压是没有 必要指定的 将来通过 习第 章后, 我们就可以从状态方程计算出一定温度 下的饱和蒸气压。不 过用 RK 方程计算 饱和蒸气压 的误差很大,应该选用能同 3.5 也由古 380K 420K . . .2.0MPa - - - - 2.25MPa ll m o l m . Mwm l 例图 图解法求状态方程的根 时适合于气、液相的状态方程,如 SRK PR MH-81 等状态方程 一般状态方程的常数都是有单位的,计算时要特别注意单位 的统一。 计算方程常数时所 用的丸、 的单位应与状态变量 的单位保持一致;而且所用单位还决定了 普适气体常数 的取值,如表 2-1 2-1 气体常数 变量单位 普适气 和卢 Pa m3 • mo[- l K 8.3 14 J • mo[- l • K- l MPa cm3 • mol- 1 K 8.3 14 MPa ' m3 • mo[-l • K-l bar cm3 • mol- 1 K 83 . 14 ba r' cm3 • mo[-l • K-l cm3 • mo[- l K 82 . 06 atm' cm3 • mo[- l • 一般情况下,应尽可能采用国际单位制 2.6 混合法则 人们总是首先针对纯物质研究并获得状态方程,这些含特征参数(如方程常数、临界参 数等)的状态方程能用于纯物质 jrV-T 或其他热力学性质计算 在研究混合物的性质时, 通常将均相棍合物看成一个虚 拟的纯物质,并具有虚拟的特征参数, 用这些虚拟的特征参数 代入纯物质的状态方程中,就可以计算?昆合物的性质了 但是, 11昆合物的虚拟参数强烈地依 赖于混合物的组成 所谓?昆合法则,就是指混合物的虚拟参数与混合物 的组成和相应的纯物 质的参数之间的关系式 ?昆合法则的建立虽有 定的理论基础,但是目前尚难以完全从理论上得到混合法则 常是在 定的理论指导下,引入适当的经验修正,再结合实验数据才能将?昆合法则确定 下来 需要指出的是,泪合物系统所用的符号的形式将有别于纯物质系统 对于纯物质系统, 般没有必要使用代表组分的下标 对于混合物系统,带有相同下标(常简化为单个下标) 者,如 "i" "j" 的均是指 昆合物中的纯组分 的性质;带有不同下标者,如 "zj" 系指 的相互作用项;没有下标者是指混合物的性质 。为 了统 起见,在以后的章节中 也是如此规定 如有某一摩尔性质 M(T 抖,在纯物质系统和?昆合物系统的符号和含义的规

20化工热力学 定如表2-2所示。 表22纯物质和混合物系统的符号和含义规定 系统 M 摩尔性质 纯物质 M 总性质,M,=M(对于均相封闭系统M与M的比是一常数) M 混合物的摩尔性质 M,(或M) 混合物中组分:的摩尔性质,与混合物同温同压 混合物 M 混合物中组分了与组分;的交叉相互作用性质(≠》 M 混合物的总性质,M,=nM(在酸开系统将会使用总性质) 2.6.1 virial方程的混合法则 由于virial方程可以从统计力学推导证明,故它的混合法则具有理论依据。第二virial 系数的混合法则通式为 B=片 yiyjBu (2-33) 一般B可以从同温度下的纯组分的iral系数B:和B,得到。若取它们的数学平均值 即B,-B十B,代入式(2:3)中得 2 (2-34) 若取它们的几何平均值,即B。=(B,B;)a5,代入式(2-33)得 B=(B卧 (2-35) 因为vial方程具有一定的理论基础,它的混合法则也为其他状态方程的混合法则的建 立提供了一定的指导意义。 2.6.2立方型方程 以vdW方程为代表的两参数立方型状态方程的常数b和a具有一定的物理意义。b与分 子的大小有关,几乎所有的状态方程都采用与式(234)等价的混合法则 (2-36) 参数4是分子间相互作用力的度量,常采用式(2-35)的形式,但各方程略有不同。如 RK方程: -(a (2-37) 而SRK方程和PR方程的常数a采用了式(2-33)的混合形式 (2-38) 为了得到更符合实验数据的结果,在交叉相互作用项中引入了相互作用参数,即 ag=√aa(1-kg) (2-39)
20 I 化工热力学 定如表 2-2 所示。 2- 质和混合物系统的符号和含义规定 M 摩尔性质 纯物质 M, 总性质, =nMC 对于均相封闭系统 ,与 的比是一常数 M 混合物的摩尔性质 iC ii 混合物中组分 尔性质,与混合物同温同压 混合物 M ij 混合物中组分 的交叉相互作用性质 (i j) M, 物的总性 nMC 在敞开系统将会使用总性质 2. 6. 1 virial 方程的混合法则 由于 vir al 方程可以从统计力学推导证明,故它的混合法则具有理论依据。第二 virial 系数的混合法则通式为 N N B = ~~ ij (2-33 ) i~l j~l 可以从同温度下的纯组分的 vir al 系数 Bi Bj 得到 若取它们的数学平均值 ZJ==-z 代入式 33 )中得 N B = ;B i i = l 若取它们的几何平均值,即 ij = (BiB j ) 0. ,代人式 (2-33 )得 N B = (~Y B? 5 r (2-34) (2-35 ) 因为 iri 方程具有 定的理论基础, 它的混合法则也为其他状态方程的泪合法则的建 立提供了 定的指导意义 2.6. 2 立方型方程 vdW 方程为代表的两参数立方型状态方程的常数 具有 定的物理意义 与分 子的大小有关,几乎所有的状态方程都采用与式 (2-34 价的混合法则 N b = ~ Y ib i (2- 36) 参数 是分子间相互作用力的度量,常采用式 (2 35 )的形式,但各方程略有不同 RK 方程 )2 SRK 方程和 PR 方程的常数 用了式 (2 33) 的混合形式 = ~~l 为了得到更符合实验数据的结果,在 叉相 作用项中引入了相 用参数句,即 (lb) (2-37) (2-38 ) ( 2-39)

第2章P水T关系和状态方程21 式(2-39)中的k,是相互作用参数,当=j时,即同分子之间的相互作用参数,k,=0。 当≠与时,代表了不同分子之间的相互作用。k与k#并不一定相等,但大多数的情况下作 为相同处理,即k。=飞。它们的数值一般从混合物的实验数据拟合得到。当然也可以从混 合物的第二virial系数的数据来决定。 2.6.3BWR方程 BWR方程的混合法则可以写成如下的通式 x=(xx (2-40) 其中,r的数值见表2-3(注意:BWR方程的混合法则还有其他的形式)。 表2-3BWR方程混合法则通式(2-40)中的r值 Ao B C。 2 1 2 3 3 32 2.6.4MH-81方程 目前,MH-81方程采用温度函数混合法则。该混合法则的建立显然也受到了virial方程 混合法则的影响。具体的形式如下 yiy;F2(T)a F2 (T)=-(1-Q)F:(T)F2(D)j F(D=(-1)1(2[w1F,(TD](k=3,4,5) (2-41) 其中,Q是二元相互作用参数。显然,Q=Q,=0,而且,大多数情况下,Q,=Q,故 对于二元混合物,只有一个二元相互作用参数Q12。混合法则式(2-41),使混合物状态方程 的温度函数与纯物质相应的温度函数保持相同的符号。一般条件下,纯物质的MH-81方程 的温度函数的符号有下列的规律: F(T)>0:F2(T)<0:F3(T)>0:Fa(T)<0:F3(T)>0 对MH方程曾经也有人建议采用临界参数混合法则和方程常数混合法则,但现使用 不多 *2.7状态方程体积根的求解 用状态方程计算流体的热力学性质时,求解状态方程的根是一个最基本的计算单元,如何正确、快速 地求出状态方程的体积根是热力学性质计算成败的关键步骤之一· 2.7.1状态方程体积根在p-V图上的几何形态 一般,以p为显函数的立方型状态方程,如SRK方程式(214)可以化为
关系和状态方程 I 21 (2 39 )中的 是相互作用参数,当 时,即同分子之间的相互作用参数,走。 =0 时,代表了不同分子之间的相互作用 并不一定相等,但大多数的情况下作 为相同处理,即 hzJ= Jl 它们的数值一般从混合物的实验数据拟合得到 当然也可以从 合物的第二 iri 系数的数据来决定 2.6.3 BWR 方程 BWR 方程的混合法则可以写成如下的通式 x = (~Y + r (2-40) 其中 的数值见表 2-3 (注意 BW 方程的混合法则还有其他的形式) 2-3 BWR 方程混合法则通式 (2-40) 中的 X Ao Bo Co a b α Y r 2 2 3 3 3 2 2.6.4 MH-81 方程 目前, MH-81 方程采用温度函数混合法则 亥?昆合法则的建 显然也受到了 iri 方程 混合法则的影响 具体的形式如下 N N F2 ( T) = ~ ~Y YjF T) j i = 1 j = l F2 (T) ij = - (1 - Qij ) ,) 1 F 2 (T) T)j 1 川=川 N b = ι 其中, ij 是二元相互作用 显然, Q ù = Qjj 而且,大多数情况下, Q ij 对于二元;昆合物,只有 元相互作用 12 混合法则式 (2 1) ,使 昆合物状态方程 的温度函数与纯物质相应的温度函数保持相同的符号 。一 般条件下,纯物质的 MH 81 方程 的温度函数的符号有下列的规律: F 1 (T) > O; F2 (丁 0; T) 0; (T) O; F5 ( T) > 0 MH 方程曾经也有人建议采用临界参数混合法则和方程常数混合法则,但现使用 不多 *2. 7 状态范程体积极的求解 用状态方程计算流体的热力 性质时,求解状态方程的根是 个最基本的计算单元, 如何 正确、快速 地求出状态方程的体积根是热力学性质计算成败的 键步骤之一。 2. 7. 1 状态方程体积根在 p-v 图上的几何形态 般,以 为显函数的 方型状态方程,如 SRK 方程式 2- 14) 可以化为

22|化工热力学 V3-RTv+(g-F-饭Iv-b=0 (2-42) 的关于V的三次方程,在组成和T、p的数值给定时,方程式(2-42)最多可以有三个根。这些根随着T 数值的不同而变化。但是,有物理意义的根一般只有两种情况:a,三个实根,b.一个实根和两个复根。 在T和组成给定的条件下,p与V的关系曲线(即等温线)可以表示在pV图上。以方程式(2 42)为例说明,由于SRK方程式(214)的分母在V-0和V一士b时为三个零点,pV图上的等温线 分为了四段,如图2-4所示。其中,只有第I段才有物理意义,为此在图25中着重讨论第段,这 是Ar在120K(其T:=150.8K,力。=4.235MPa)时等温线,此时方程式(2-14)的常数a= 154640.34Mpg,cm5.m0l-2,h=22.3rm3,m0l-1 对于体积很小的区域,等温线是很陡的。当V→b=22.30cm3·mol1时,力→∞:随着V从 2.30cm3 mol 开始增加时,p快速下降,直到最低点②,此时p:=一7.112MPa,V:=45.73cm mol-1。随着V的进一步增加,p又开始上升,直到极大值点④,此处p-2.15MPa,V,-215.5cm3· mo一1。之后,p随着V的增加而单调下降,当Vo©时,p+0。 由图2-5可知,120K的Ar在0<p<2.15MPa的压力范围内有三个正的实数根。其中最小的根代表液 相体积,最大的代表蒸气体积,中间的根没有物理意义,因为处于该根邻城的等温线具有正的斜率,不符 合热力学的稳定性条件。 80 40 200 400 600 (emmot-l -8.0⑦ =0 图2-4SRK立方型状态方程在 图2-5Ar的SRK方程等温线和 pV图上的亚临界等温线 蒸气压(T-120K) 在上述的压力范围内,每个压力都对应着一对液相和气相根,但其中只有一对根是代表气液两相共存 的平衡,该压力就是饱和蒸气压力,它符合Maxwell等面积规则(第4章将会证明) 50四-①=50①0-① (2-43) 式(2-43)等价于 D(T.V)dV-p(vm-v) (244) 不仅如此,式(2-43)或式(2-44)也等价于纯流体的汽-液平衡条件,G(T,V)=G(T,V)。它们与状态方 程的结合可以用于求解纯物质的蒸气压p和其他饱和性质(如V、V等): 在式(244)中,p(T,)是状态方程,即图25中的等温线,V和V是状态方程的饱和气、液相体 积根,即①点和⑤点的摩尔体积, 女V图上状态方程的超临界等温线和临界等温线如图26所示。其的曲线为气液两相共存区的边界线 由于T>工。的等温线是随着摩尔体积的增加而单调下降,故对任何一给定的压力p,只有一个体积根V
22 I RT_o , bRT _ ab ~VZ+ -b' 一一一 IV一一 =0 (2-42) 户飞 的关于 的三次方程,在组成和 的数值给定时,方程式 (2 42 )最多可以有 个根 这些根随着 户数值的不同而变化 但是,有物理意义的根 般只有两种情况: 三个实根; 个实根和两个复根。 和组成给定的条件下 的关系曲 线( 即等温线)可以表示在 jrV 图上 以方程式 (2 42) 为例说明,由于 SRK 方程式 (2-14 的分母在 V= V= 士 时为三个零点,户 图上的等温线 分为了四段,如图 所示 其中,只有第 段才有物理意义。为此在图 中着重讨论第 段,这 Ar 120K (其 = 150. 8K , Pc = 4. 235MPa) 时等 温线,此时方程式( 2-14 )的常数 154640. 34MPa' cm6 • mol- z ; b=22.3cm3 • mo 对于体积很小的区域,等温线是很陡的。当 = 22. 30cm3 • mol 时,户→ ;随 22.30cm3 • mo 开始增加时, 快速 降,直到 低点 ,此时 7. 112MPa, Vz = 45. 73cm3 • mol- 1 随着 的进一步增加,户叉开始上升,直到极大值点④,此处向 2. 15MPa , V4 = 215. 5cm3 • mo 之后 随着 的增加而单调下降,当 由图 -5 可知, 120K Ar 2.15MPa 的压力范围内有三个正的实数根。其中最小的根代表液 相体积,最大的代表蒸气体积,中间的根没有物理意义,因为处于该根邻域的 温线具有正的斜率 ,不 合热力学的稳定性条件 U SRK 立方型状态方程在 图上的亚临界等温线 V 8.0 4.0 (吊 ④ pS 里。 j:0 200 400 600 V/(cm3'mol- 1) :H Ar SRK 方程等温线和 蒸气压 120K) 800 在上述的压力范围 内, 每个压力都对应着 对液相和气相 根,但其中 只有一对根 表气液两相共存 的平衡,该 力就是饱和蒸气压扩。 它符合 axwell 等面积 则(第 章将会证明) S( -(-(-( =s(-(j)-( -( (2-43 ) (2-43 )等价于 ,1 p(T,V )dV = pS(ysv - v sl) (2-44) V 不仅如 此, (2-43 )或式 2-44 )也 纯流体的 平衡条件,以 v sl ) = G( T , V) 。它 状态方 程的结合可以用于求解纯物质的蒸气压扩和其他饱和性质(如 sl SV 等) 在式 (2 44 )中 p(T, V) 是状态方程,即图 中的等温线 SV 是状态方程的饱和气 液相体 积根,即 点和 摩尔体积 jrV 图上状态方程的超临界 和临界 所示。其虚的曲 线为气液两相共存区的边界线 温线是随着摩尔体积的增加而单调下降,故对任何 给定的压力扩 有一个体积根
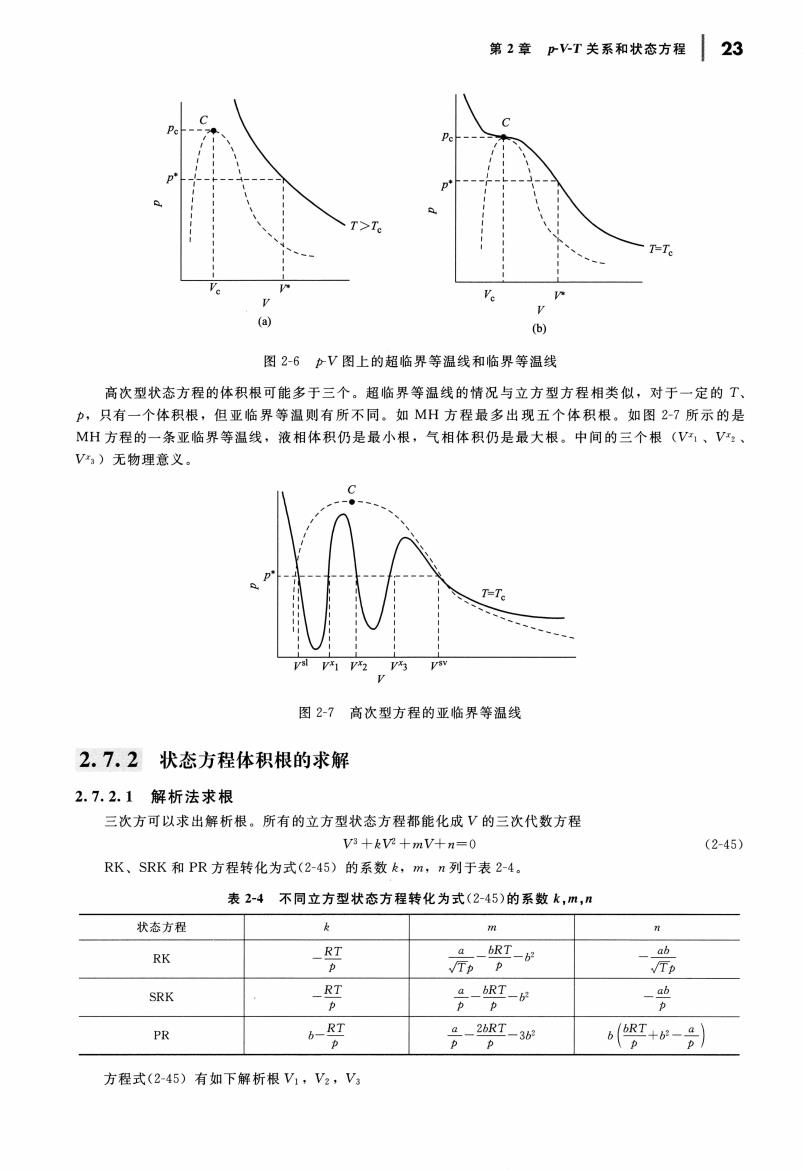
第2章PT关系和状态方程23 6) 图2-6力V图上的超临界等温线和临界等温线 高次型状态方程的体积根可能多于三个。超临界等温线的情况与立方型方程相类似,对于一定的T p,只有一个体积根,但亚临界等温则有所不同。如M州方程最多出现五个体积根。如图2-7所示的是 MH方程的一条亚临界等温线,液相体积仍是最小根,气相体积仍是最大根。中间的三个根(V,V、 V)无物理意义. 内 图2-7高次型方程的亚临界等温线 2.7.2状态方程体积根的求解 2.7.2.1解析法求根 三次方可以求出解析根。所有的立方型状态方程都能化成V的三次代数方程 V5十kV2+mV+n=0 (2-45) RK、SRK和PR方程转化为式(245)的系数k,m,n列于表24. 表2-4不同立方型状态方程转化为式(2-45)的系数k,m,” 状态方程 RK 六 元 SRK 片- PR 6+- 方程式(245)有如下解析根V1,V2,V
Pc ,、 .' p.~ -J- 气- l I 、; ;!\i I 、也 、 Vc V‘ V (a) 民‘ p-'-ιT 关系和状态方程 C pJ-~ :、\ p· -J-1- 斗-丁 Jli 丁\ e l i\\ v c F V (b) T= p- 图上的超临界等温线和临界等温线 23 高次型状态方程的体积根可能多于三个。超临界等温线的情况与立方型方程相类似,对于一定的 户,只有 一个体积根, 但亚临界等温则有所不同 MH 方程最多出现五个体积根 如图 2-7 所示 的是 MH 方程的 一条亚 临界等温线,液相体积仍是最小根,气相体积仍是最大根 中间的 三个根 (V" V"3 )元物理意义。 VXz VX3 VSV y 高次型方程的亚临界等温线 2.7.2 状态方程体积根的求解 2.7.2.1 解析法求根 次方可以求出解析根。所有的立方型状态方程都能化成 的三次代数方程 V3 + kVZ + mV+n=O RK SRK PR 方程转化为式 (2 45 )的系数 m , 列于表 -4 2-4 不同立方型状态方程转化为式 (2-45 的系数 状态方程 k η1 RK RT RT_ J. /Tp p SRK RT 三二 bRT-b' p p PR b RT 2bRT 3bz p 方程式 (2 45 )有如下解析根叭,町,只 (2-45 ) 11 αb 汀户 αb p b(~iT ;)