
明 肥市第五中学 Hefei No.5 Senior High School 理驾学 3.2.1抛物线及其 善行健美 标准方程 王茹
王茹 3 . 2 . 1抛物线及其 标准方程

复 习 1.椭圆的定义 平面内与两个定点F1,F2的距离之和等于 常数2,(2>|F1F2)的点的轨迹叫做椭圆. 2.双曲线的定义 平面内与两个定点F1,F2的距离之差的绝 对值等于常数2a,(2M<F1F2)的点的轨迹 叫做双曲线
平面内与两个定点F1 ,F2的距离之和等于 常数2a,(2a>|F1F2 |)的点的轨迹叫做椭圆. 平面内与两个定点F1 ,F2的距离之差的绝 对值等于常数2a,(2a<|F1F2 |)的点的轨迹 叫做双曲线. 1.椭圆的定义 2.双曲线的定义 复 习


抛物线画法 西视频 观察动画,概括 动点P满足的条 件: 绘制抛物线动画演示 结论:①在平面 m亚=397厘米 内,动点P到定点 ml丽-3.97厘米 N的距离与到定直 线的距离相等, 课件制作微信Lay100 即PN=|PM. ②点P的轨迹形状 与二次函数的图 像相似
观察动画,概括 动点P满足的条 件: 结论:①在平面 内,动点P到定点 N的距离与到定直 线l的距离相等, 即|PN|=|PM|. ②点P的轨迹形状 与二次函数的图 像相似. 抛物线画法
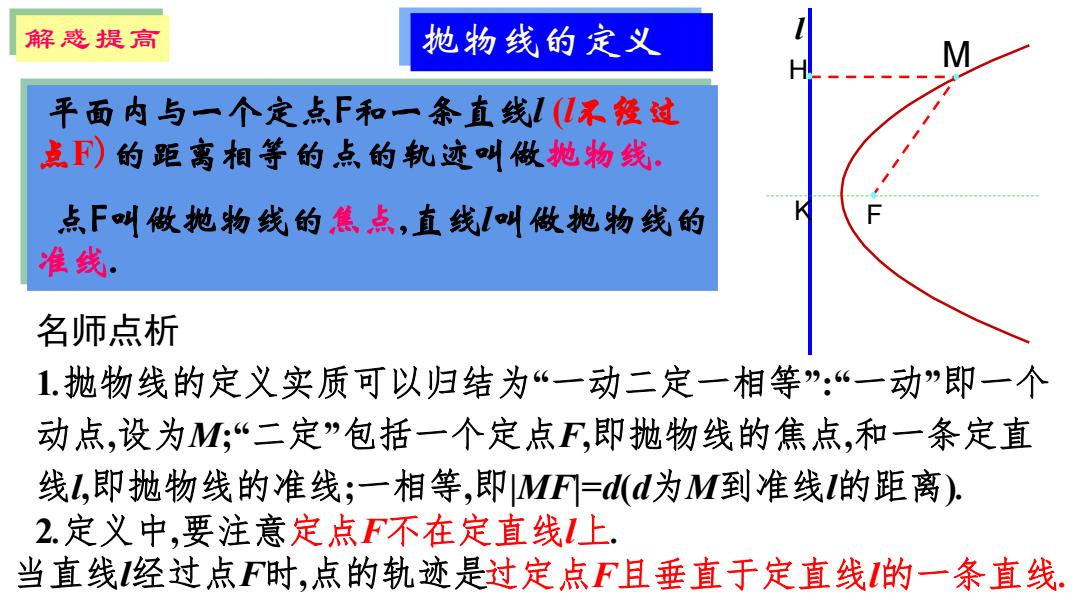
解惑提高 抛物线的定义 平面内与一个定点F和一条直线(U不:过 点F)的距离相等的点的轨迹叫做抛物线: 点F叫做抛物线的焦点,直线叫做抛物线的 准线。 名师点析 1抛物线的定义实质可以归结为“一动二定一相等”:“一动”即一个 动点,设为M;“二定”包括一个定点F,即抛物线的焦点,和一条定直 线L,即抛物线的准线;一相等,即MF=dd为M到准线的距离). 2.定义中,要注意定点F不在定直线1上. 当直线经过点F时,点的轨迹是过定点F且垂直于定直线的一条直线
抛物线的定义 l K F H M 平面内与一个定点F和一条直线l (l不经过 点F)的距离相等的点的轨迹叫做抛物线. 点F叫做抛物线的焦点,直线l叫做抛物线的 准线. 名师点析 1.抛物线的定义实质可以归结为“一动二定一相等”:“一动”即一个 动点,设为M;“二定”包括一个定点F,即抛物线的焦点,和一条定直 线l,即抛物线的准线;一相等,即|MF|=d(d为M到准线l的距离). 2.定义中,要注意定点F不在定直线l上. 当直线l经过点F时,点的轨迹是过定点F且垂直于定直线l的一条直线. 解惑提高