电子科技大学：《遥感图像处理 Remote Sensing Image Processing》课程教学资源（课件讲稿）第五章 遥感图像的校正与定标

仿射变换可以用于卫星传感器变形的近似 校正(Anuta,1973;Steiner and Kirby, 1976;Richards and Jia,1999)。如下表是 几个用于校正Landsat MSS图像传感器和轨道 相关的变形的仿射矩阵 表7.1 针对Landsat MSS数据的特殊仿射变换(Anuta,1973;Richards and Jia,1999)所用到 的各种角度为：：在赤道处的轨道倾角（度）；中：景中心地理纬度：0：在纬度中处的轨 道倾角，日=90-acos[sin i/cos中]（度）；Y:由于地球旋转引起的图像上下侧斜角 变形 变换矩阵 注 解 纵横比 =0.709GS 地球自转 ,a=tan 7 cos÷cos0 x方向剪切 指北旋转 cos 0 -sin 07 sin 0 cos 0 地图定向 16

16 仿射变换可以用于卫星传感器变形的近似 校正（Anuta, 1973; Steiner and Kirby, 1976; Richards and Jia, 1999）。如下表是 几个用于校正Landsat MSS图像传感器和轨道 相关的变形的仿射矩阵 UESTC-RSIP

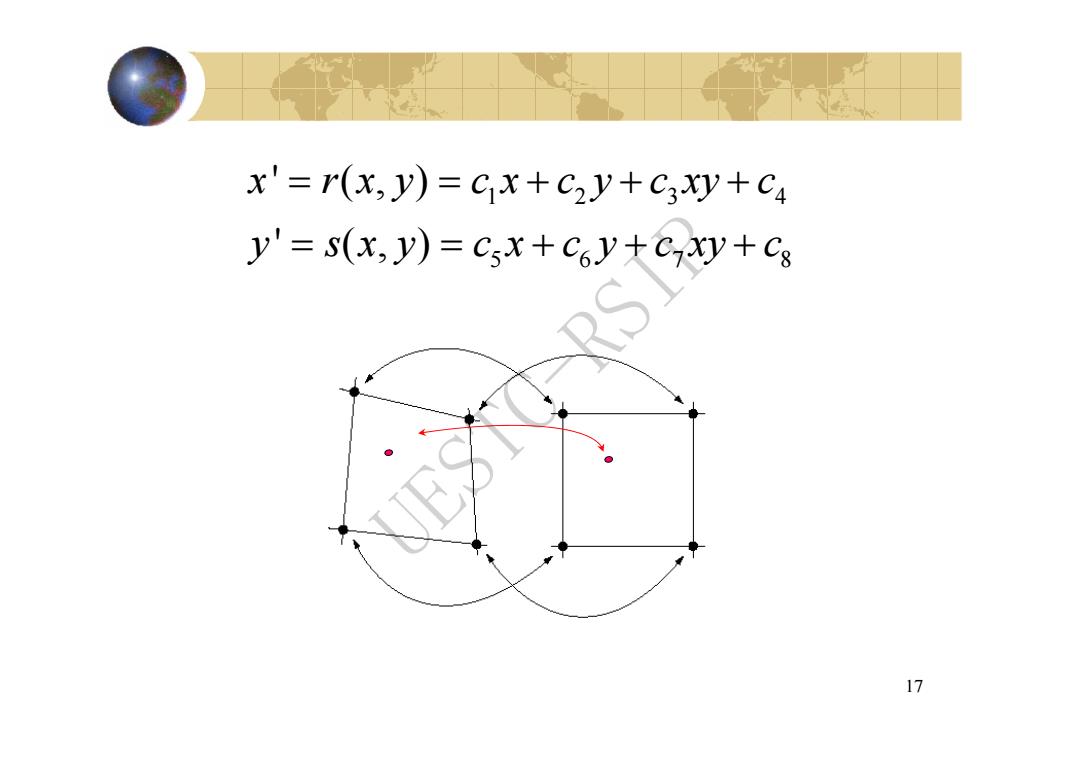
x'=r(x,y)=cx+c2y+c3xy+c4 y'=s(x,y)=Csx+Coy+cxy+Cs 17

17 12 3 4 567 8 ' (, ) ' (, ) x r x y c x c y c xy c y s x y c x c y c xy c        UESTC-RSIP

假设几何变形模型为二次多项式模型 x'=aoo+aox+doy+axy+aox2+ao2y? y=boo+box+bo1+b+box+bo2 假设从畸变图像和参考图像中←共选取了M对GCP(Ground Control Point) doo [boo 为 Xy x 1 为 x乃 x 1 X2 y2 X2V2 X> X2 2 X2Y2 x 片 : XMYM x a20 1 XMYM x 0 18

18 2 2 00 10 01 11 20 02 2 2 00 10 01 11 20 02 ' ' x a a x a y a xy a x a y y b b x b y b xy b x b y           假设几何变形模型为二次多项式模型 假设从畸变图像和参考图像中一共选取了M对GCP(Ground Control Point) 00 ' 2 2 1 11 1 111 10 ' 2 2 2 22 2 222 01 11 ' 2 2 20 02 1 1 1 M M M MM M M a x x y xy x y a x x y xy x y a a x x y xy x y a a                                          00 ' 2 2 1 11 1 111 10 ' 2 2 2 22 2 222 0111 ' 2 2 2002 111 M M M MM M M b y x y xy x y b y x y xy x y bb y x y xy x y bb                                   UESTC-RSIP      

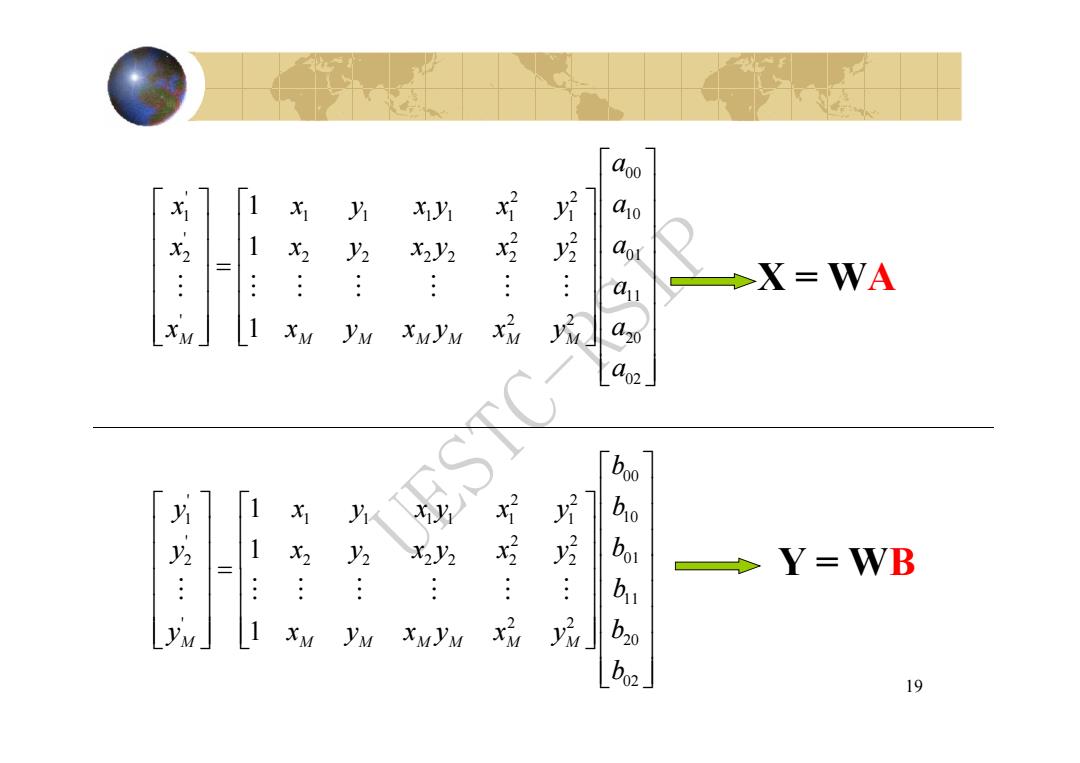
doo 1 X1 y X乃 x好 1 X2 y2 X2Y2 .: .… X=WA 1 XM yM XMYM x品 [bo 川马 1 x好 … y2 Y=WB 1 XM XMYM 19

19 00 ' 2 2 1 11 1 111 10 ' 2 2 2 22 2 222 01 11 ' 2 2 20 02 1 1 1 M M M MM M M a x x y xy x y a x x y xy x y a a x x y xy x y a a                                            X=W A Y=W B 00 ' 2 2 1 11 1 111 10 ' 2 2 2 22 2 222 01 11 ' 2 2 20 02 1 1 1 M MMM MMM b y x y xy x y b y x y xy x y b b y x y xy x y b b                                            UESTC-RSIP

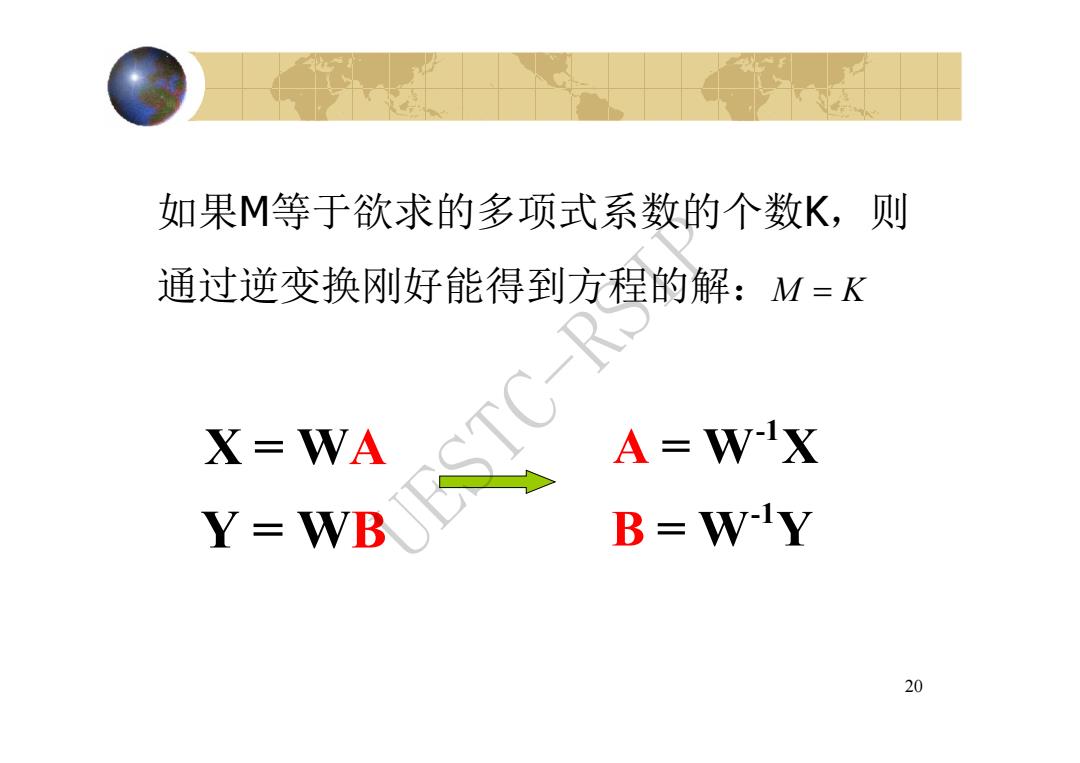
如果M等于欲求的多项式系数的个数K,则 通过逆变换刚好能得到方程的解：M=K X=WA A=W-X Y-WB B=W-Y 20

20 如果M等于欲求的多项式系数的个数K，则 通过逆变换刚好能得到方程的解： -1 -1 A B =W X =W Y M  K X=WA Y=WB UESTC-RSIP