
2.热力学平衡态当系统的诸性质不随时间而改变,则系统就处于热力学平衡态,它包括下列几个平衡:(1)热平衡(thermal equilibrium)系统各部分温度相等(2)力学平衡(mechanicalequilibrium)系统各部的压力都相等。如有刚性壁存在,虽双方压力不等,但也能保持力学平衡(3)相平衡(phaseequilibrium)多相共存时,各相的组成和数量不随时间而改变(多种固体不能混为一相,例如:大米面+黄米面;气体无论多少种都能混为一相)(4)化学平衡(chemicalequilibrium反应系统中各物的数量不再随时间而改变
当系统的诸性质不随时间而改变,则系统就 处于热力学平衡态,它包括下列几个平衡: (1)热平衡(thermal equilibrium) 系统各部分温度相等 (2)力学平衡(mechanical equilibrium) 系统各部的压力都相等。如有刚性壁存在,虽双方压 力不等,但也能保持力学平衡 2.热力学平衡态 (3)相平衡(phase equilibrium) 多相共存时,各相的组成和数量不随时间而改变 (多种固体不能混为一相,例如:大米面+黄米面 ;气体 无论多少种都能混为一相) (4)化学平衡(chemical equilibrium ) 反应系统中各物的数量不再随时间而改变

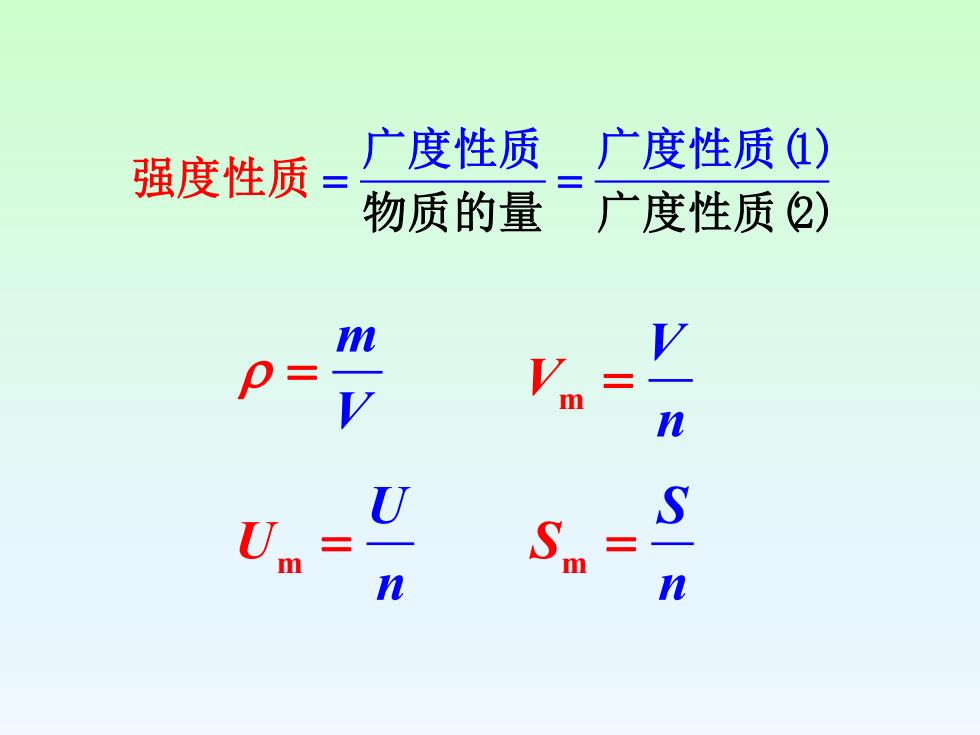
3.系统的性质用宏观可测性质来描述系统的热力学状态,故这些性质又称为热力学变量。可分为两类:(1)广度性质(extensiveproperties又称为容量性质,它的数值与系统的物质的量成正比如体积、质量、炳等。这种性质有加和性,在数学上是一次齐函数。(2)强度性质(intensiveproperties)它的数值取决于系统自身的特点,与系统的数量无关,不具有加和性,如温度、压力、密度、黏度等。它在数学上是零次齐函数。指定了物质的量的容量性质即成为强度性质,或两个容量性质相除得强度性质
用宏观可测性质来描述系统的热力学状态,故这些 性质又称为热力学变量。可分为两类: (1)广度性质(extensive properties) (2)强度性质(intensive properties) 3.系统的性质 又称为容量性质,它的数值与系统的物质的量成正比, 如体积、质量、熵等。这种性质有加和性,在数学上是 一次齐函数。 它的数值取决于系统自身的特点,与系统的数量无关,不具有 加和性,如温度、压力、密度、黏度等。它在数学上是零次齐 函数。指定了物质的量的容量性质即成为强度性质,或两个容 量性质相除得强度性质
广度性质广度性质(1)一强度性质一广度性质2)物质的量mVO:mnSUSUmmnn
Um U n = = = 广度性质 广度性质(1) 物质的量 广度性 强度性质 质(2) m V = Vm V n = Sm S n =

4.状态函数(statefunction)系统的一些性质,其数值仅取决于系统所处的状态,而与系统的历史无关:它的变化值仅取决于系统的始态和终态,而与变化的途径无关。具有这种特性的物理量称为状态函数。(1)状态函数与状态的关系状态确定全部状态函数确定口状态改变,不一定所有的状态函数都改变;但只要有一个状态函数改变,则状态即发生了改变。口状态函数之间互有联系纯物质均相封闭系统,无化学变化时,只需两个强度性质和物质的量即可确定系统的状态
系统的一些性质,其数值仅取决于系统所处的状态,而 与系统的历史无关;它的变化值仅取决于系统的始态和终 态,而与变化的途径无关。具有这种特性的物理量称为状 态函数。 4. 状态函数(state function) (1)状态函数与状态的关系 状态确定 全部状态函数确定 状态改变,不一定所有的状态函数都改变;但只要有一 个状态函数改变,则状态即发生了改变。 状态函数之间互有联系。 纯物质均相封闭系统,无化学变化时,只需两个强度性质 和物质的量即可确定系统的状态

(2)状态函数的基本性质口系统由始态到终态所引起的状态函数的改变量只与始末状态有关,与具体历程无关异途同归,值变相等:周而复始,数值还原状态函数在数学上具有全微分的性质z= f(x,y)az0%dz.=dx +dax
系统由始态到终态所引起的状态函数的改变 量只与始末状态有关,与具体历程无关。 异途同归,值变相等;周而复始,数值还原。 状态函数在数学上具有全微分的性质。 (2)状态函数的基本性质 z f x y = ( , ) dz = y x z z dx dy x + y