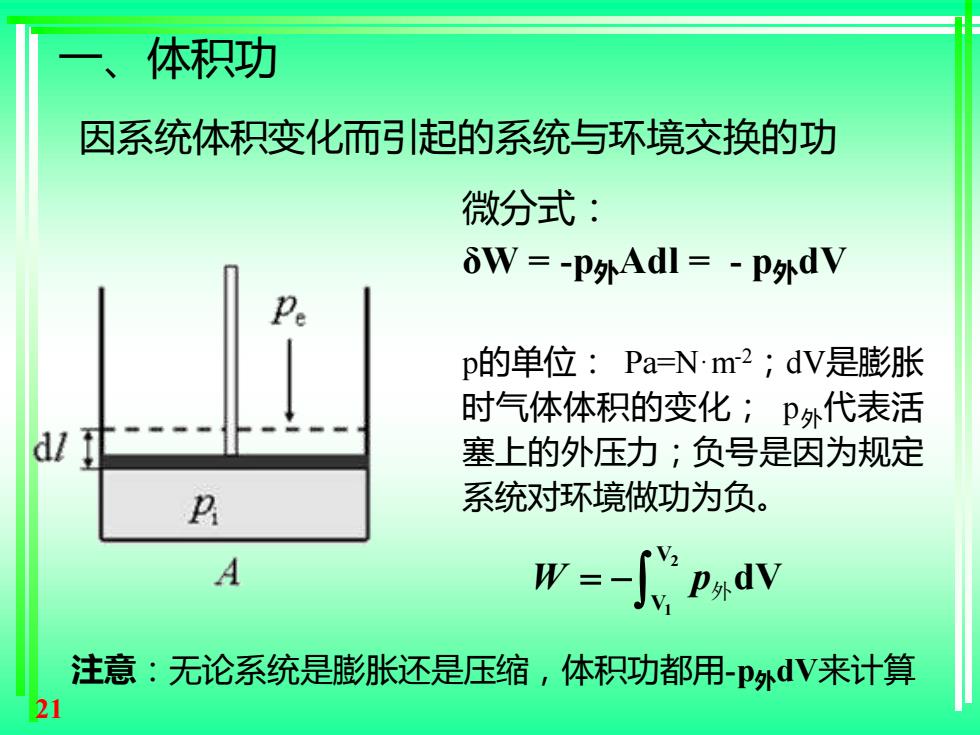
一、体积功 因系统体积变化而引起的系统与环境交换的功 微分式: δW=-P外Adl=-P外dV Pe p的单位:Pa=Nm2;dV是膨胀 时气体体积的变化;p外代表活 dl f 塞上的外压力;负号是因为规定 P 系统对环境做功为负。 A 注意:无论系统是膨胀还是压缩,体积功都用-P外dV来计算 21
21 一、体积功 因系统体积变化而引起的系统与环境交换的功 微分式: δW = -p外Adl = - p外dV p的单位: Pa=N·m-2;dV是膨胀 时气体体积的变化; p外代表活 塞上的外压力;负号是因为规定 系统对环境做功为负。 2 1 V V W p = − 外dV 注意:无论系统是膨胀还是压缩,体积功都用-p外dV来计算
体积功 体积功不是状态性 质,而与途径有关 验证方式:一气体具有 相同的始态、终态而不 同途径的几种定温膨胀 过程,计算功的大小 途径不同,体积 功的数值不同 22
22 验证方式:一气体具有 相同的始态、终态而不 同途径的几种定温膨胀 过程,计算功的大小 体积功不是状态性 质,而与途径有关 途径不同,体积 功的数值不同 一、体积功
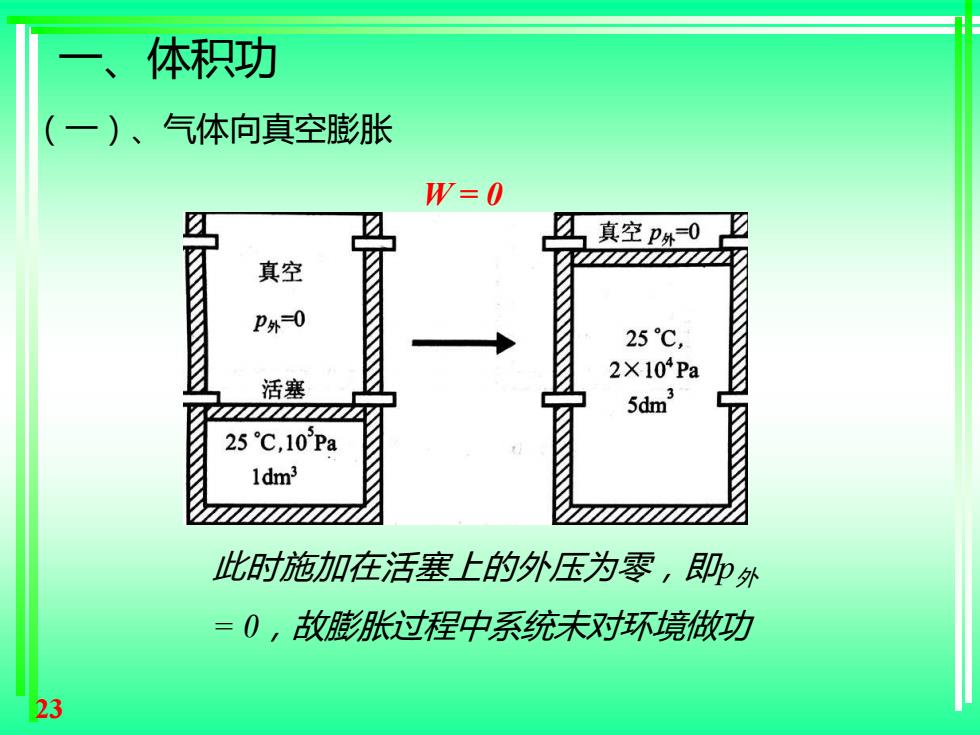
一、体积功 (一)、气体向真空膨胀 W=0 真空P外=0 真空 P外0 25℃, 2×104Pa 活塞 3 5dm 25℃,10Pa 1dm3 此时施加在活塞上的外压为零,即外 =0,故膨张过程中系统未对环境做功 23
23 (一)、气体向真空膨胀 此时施加在活塞上的外压为零,即p外 = 0,故膨胀过程中系统未对环境做功 W = 0 一、体积功
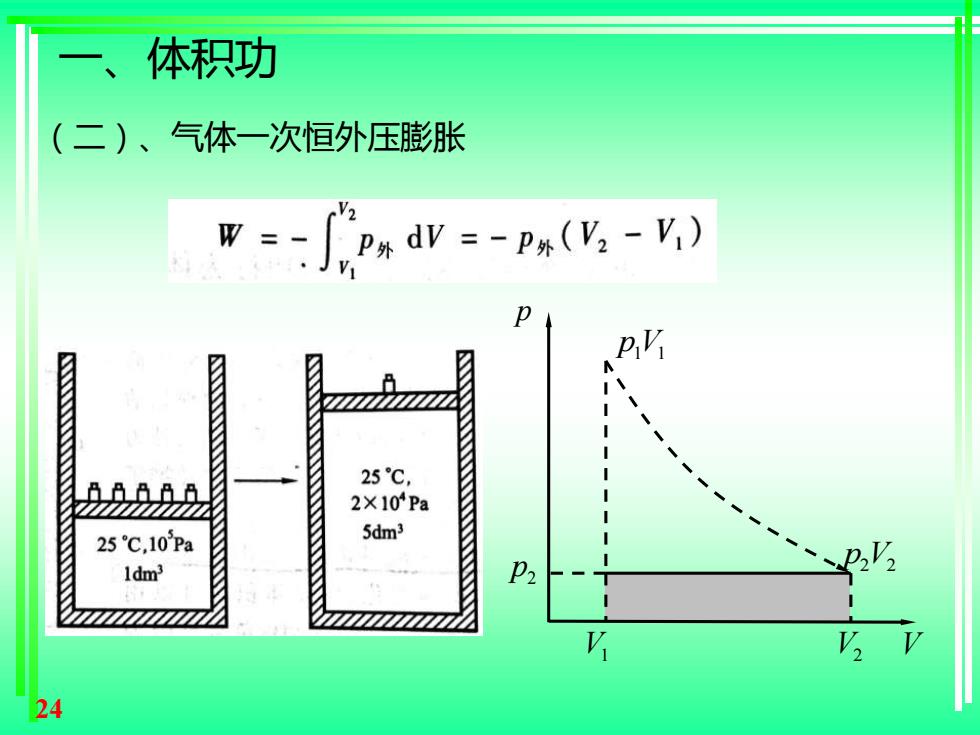
一、 体积功 (二)、气体一次恒外压膨胀 2 W=-P%dV=-P*(-V) pY 25℃, 2×10Pa 25℃,103Pa 5dm> 1dm' P2 24
24 pV1 1 2 p V1 V2 V p p V2 2 (二)、气体一次恒外压膨胀 一、体积功
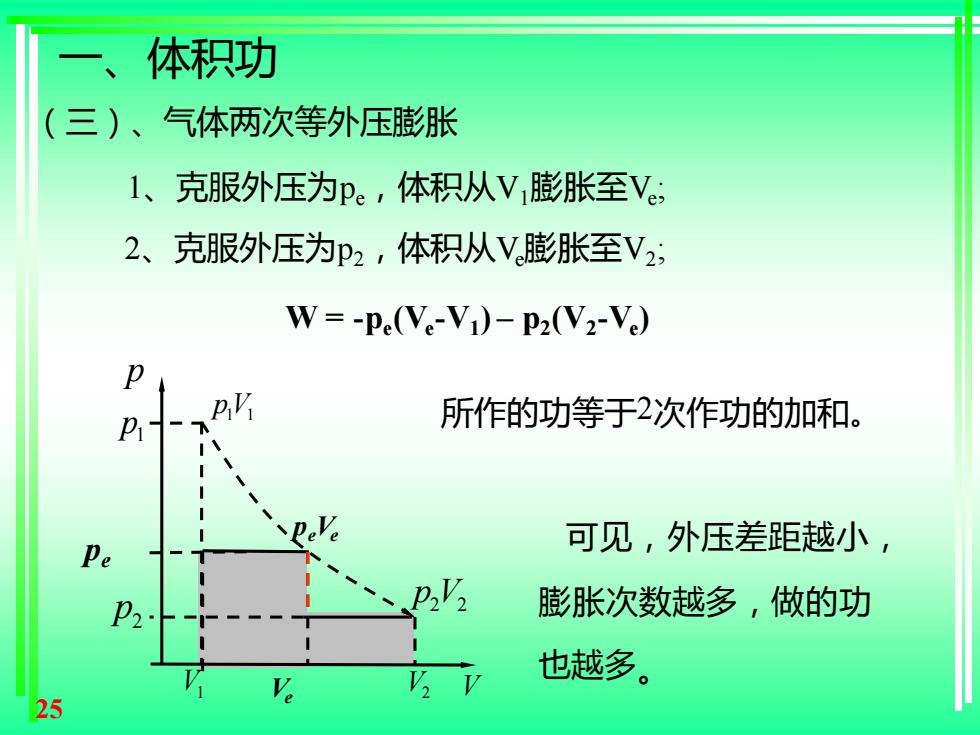
一、体积功 (三)、气体两次等外压膨胀 1、克服外压为P。,体积从V膨胀至Ve: 2、克服外压为p2,体积从V膨胀至V2; W=-Pc(Ve-V1)-p2(V2-Ve) 所作的功等于2次作功的加和。 可见,外压差距越小, p 膨胀次数越多,做的功 也越多。 25
25 1 1 pV V p 2 2 p V 1 p 2 p V1 V2 1、克服外压为pe,体积从V1膨胀至Ve ; 2、克服外压为p2,体积从Ve膨胀至V2 ; peVe pe Ve W = -pe (Ve -V1 ) – p2 (V2 -Ve ) (三)、气体两次等外压膨胀 一、体积功 可见,外压差距越小, 膨胀次数越多,做的功 也越多。 所作的功等于2次作功的加和