
第二章徽型计算机继电保护的数字信号基陆 17 734r 0727374r 图28离散系统的冲微响应 以此推算下去,在kT<r<(k+1)T时间内,系统的输出响应是 y(t)=g(t)x(0)+g(t-T)x(T) +8(t-2T).c(2T)+.+8(t-kT)x(r) 写成级数和的形式: y(t)=∑g(:-kT)x(kT)(k=0,1,2,…,n) (2-18) 现在只讨论在具体的采样时刻t一nT时,系统的输出值为 y(nt)=∑g[(n-k)T].x(T)(k=0,1,2,…,n)(2-19) 这就是离散系统的卷积形式。由于在k>时g[(n一k)T]=0,所以上式也可写 华 y(r)=∑g[(n-)Tjx(kT)(k=0,1,2,…,∞)(2-20) 利用:变换的卷积定理将式(2-20)两边取x变换,可得 Y(ε)=H(x)X(x) 即得 H(z)=Y(z)/x(a) (2-21) 其中H(x)是系统单位冲激响应g(t)的x变换。 现举例说明在已知滤波系统的方框图和差分方程埘,求取系统脉冲传递函数 的方法,并请注意脉冲传递函数与系统时域差分方程之间的转换关系,这对微机继 电保护中数字滤波器的时域算法是非常重要的

电力系统继电保护原理及新技术 例21已知G(s)=5[s(x+5)】,求系统的脉冲传递函数 解将G(s)展开成部分分式: c- 经x变换得 6)=8=,1 c(1-p7) =2-1(2-6) 例2-2设离散系统的差分方程如式(2-16)所示,系统的初始值为零,试求系 统的脉冲传递函数。 解对此差分方程两边取:变换,得 (l+d1211a2e2+…+a2*)Y(x) =(b。1b1之1+2224…+6nzm)X(z)) 整理得 (2-22) 通过此例可以看出,在已知离散系统的脉冲传递函数H(x)时,就可以很方便 地求出系统对应的时域差分方程,找出时域内系统的输人脉冲序列与系统输出咱 应珠冲序列之间的差分方礼同系统的结构特征H(:)表达式之间的关系式。 3.数字控制系统的脉冲传递函数H(:)的求法简介 脉冲传递函数H(x)可分为开环脉冲传递函数和闭环脉冲传递函数,若控制 器或系统的输人信号中不包含控制器输出量的信息,称该系统为开环数字控制系 统,其传递函数为开环脉冲传递函数,反之若输人信号中含有输出量的相关信息, 则称该系统为闭环数控系统,其传递函数为闭环脉冲传递函数,而它们的求取方法 也与连续时间控制系统的传递函数G(s)的求取方法相似。 (1)开环脉冲传递函数的求取 环脉冲传递函数根据控制系统结构的不同义可分为如下两种形式: 1)串联环节阿无采样开关,其结构如图29所示。其开环脉冲传递函数为 )=8=zG6,s】=G,) (2-23)
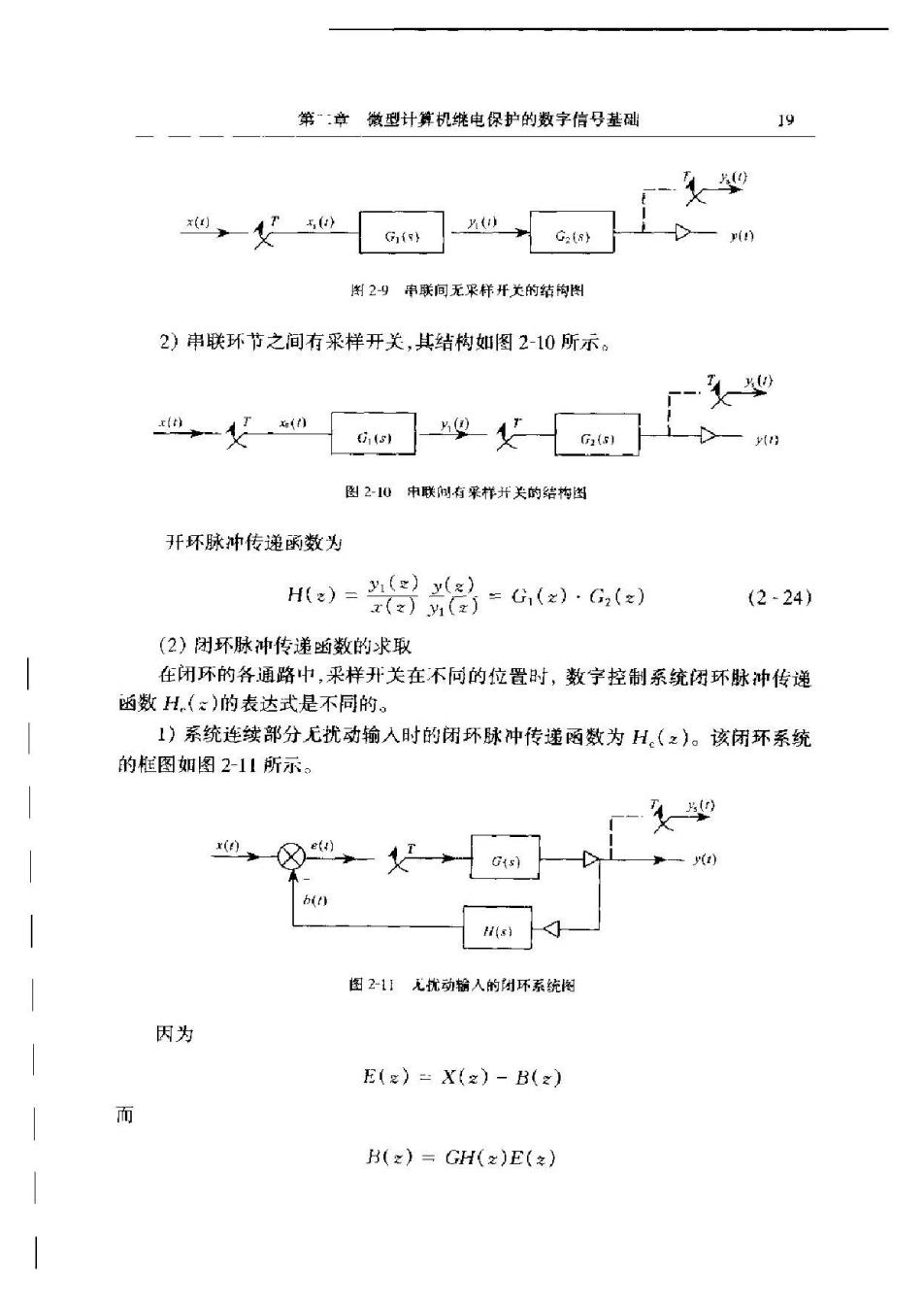
第:章微型计算机姚电保护的数字信号基础 9 ,0】> 图2)帘联间无采林开关的结向图 2)串联环节之间有采样开关,其结构如图2-10所示。 "-从w69父m☐-w 图20中联阅有采样开关的结构图 开环脉冲传递函数为 (2-24) (2)团环脉冲传递幽数的求取 在闭环的各通路中,采样开关在不同的位置时,数字控制系统闭环脉冲传递 函数H(:)的表达式是不同的。 1)系统连续部分无扰动输入时的闭环脉冲传递函数为H(z)。该闭环系统 的框图如图2-11所示。 Gu) 一a) L 图21无优动输人的闭环系统 因为 E(g)=X(z)-B(z) 而 B(z)=GH(z)E()
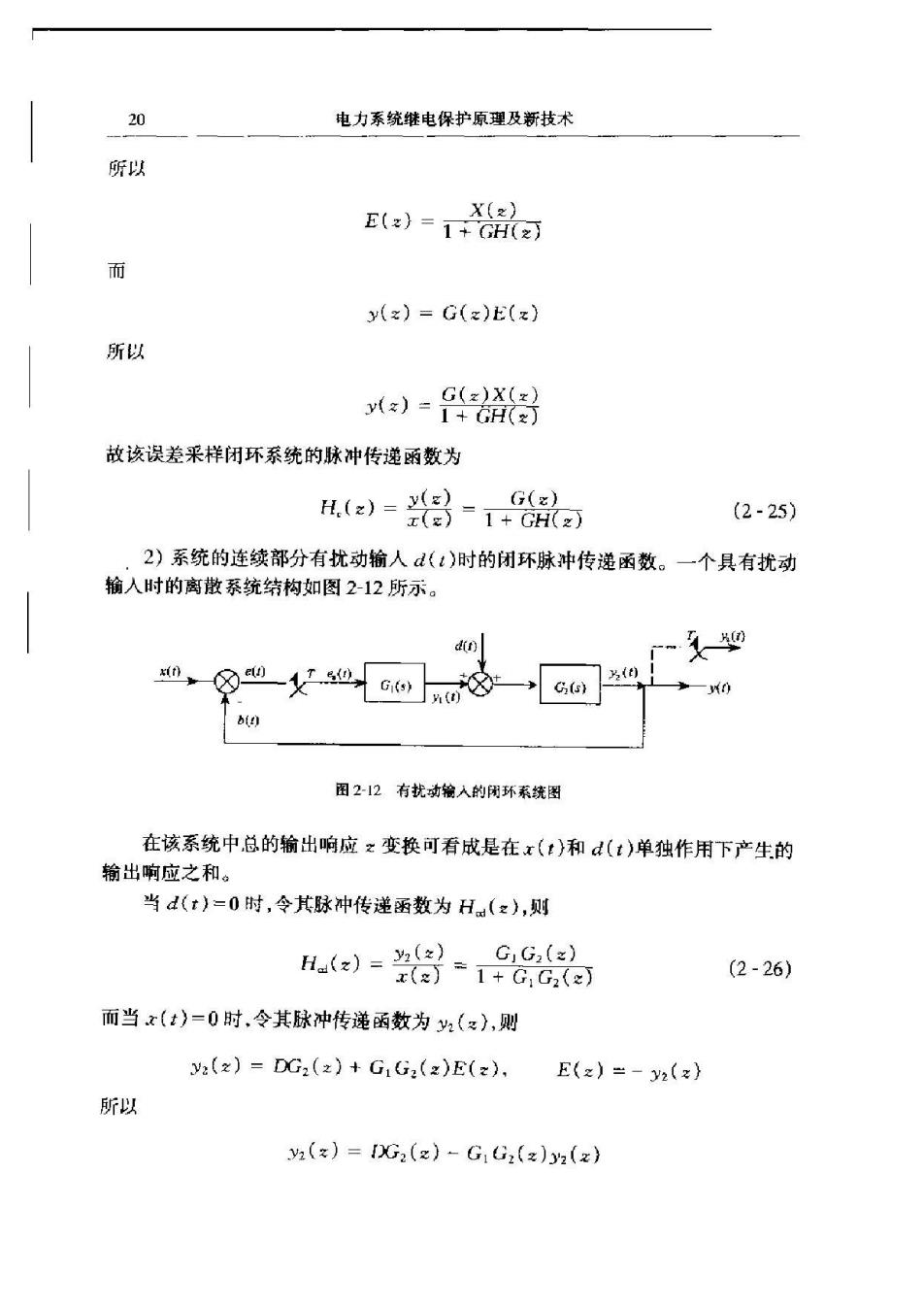
20 电力系统继电保护原理及新技术 所以 =1鼎a y(z)=G()E(z) 所以 )=8得 故该误差采样闭环系统的脉冲传递函数为 ()=铝-鼎a (2-25) 2)系统的连续部分有扰动输人d()时的闭环脉冲传递函数。一个具有扰动 输人时的离散系统结构如图212所示。 d( 一0 图212有扰动输入的用环系统图 在该系统中总的输出响应z变换可看成是在x(:)和d(t)单独作用下产生的 输出响应之和。 当d(t)=0时,令其脉冲传递函数为H(z)),则 H)=8=品% GG(x) (2-26) 而当x(t)=0时,令其脉冲传递函数为出(x),则 y2(x)=DG2(x)+G1G2(z)E(z). E(z)=-y2(x) 所以 y2(z)=DG2(z)-GG2(z)(z)

第二章微型计算机继电保护的数字信号基础 21 0行,(z) ()=1+C,G( 由于扰动d(t)与系统G,(s)间无采样开关,因此得不到该数字控制系统总的 闭环脉冲传递函数H(x)。 4.脉中待递离数零,点和极点对数字滤波器选波性能的影响 (1)零,点及其滤波作用 脉冲传递函数H(x)中分子多项式为零的方程的根,称为脉冲传递函数的零 点,在脉冲传递函数表达式中以因子(1-c,x')的形式出现,C,是H(z)的一个零 点。不难看出,该因子的频率特性表达式为 (1-ce)) (2-27) 式中,w=2π;T为采样周期。 如果在某-一特定的频率1下,即1=2x5,可以使11-c1er为零,则表 明数字涉波器的频率特性在该频率人下的值为零,数字滤波器对输人信号中的频 率为1的分量能完全滤除,即在数字滤波器的输出信号中不含有频率为∫,的信 号。 由此来看,如果要求数字滤波器滤除输人信号中频率为:的信号,则应在该 频率:处设置一个脉冲传递函数零点,即,=「;如果要求数字滤波器滤除有 限个频率f(:=1~m)的信号时,则要求数字滤波器的脉冲传递函数中应设置m 个零点,C=,m=2f,f是所要求滤除的谐被频率(1=1,2,…,m),对应的 脉冲传递函数因子为 [l(1-c2)(i=1,2,…,m) (2-28) (2)极.点及其滤波作用 脉冲传递函数H(:)中,分母多项式为零的方程的根称为脉冲传递函数的极 点,在脉冲传递函数H(e)中以因子(1-d,3)的形式出现,d,是H(z)的一个 极点。该因子的频率特性表达式为 (1-d,er) (2-29) 式中,w=2;T为采样周期。 若在某一个特定频率3上,w2=2f2,可使1-d21等于零或数值很 小,则表明数字德波器对于输入倍号中频率为的分量具有很大的幅值放大倍