
Lotka-Volterra的捕食模型 : 没有捕食者 :dN/dt =r1N 没有猎物:dP/dt =-r2P 两者共存 : dN/dt =r1N-εP N ε:压力常数,即平均每一捕食者,捕杀猎物的常数 dP/dt =-r2P+θN P θ:捕食效率常数
Lotka-Volterra的捕食模型 : 没有捕食者 :dN/dt =r1N 没有猎物:dP/dt =-r2P 两者共存 : dN/dt =r1N-εP N ε:压力常数,即平均每一捕食者,捕杀猎物的常数 dP/dt =-r2P+θN P θ:捕食效率常数
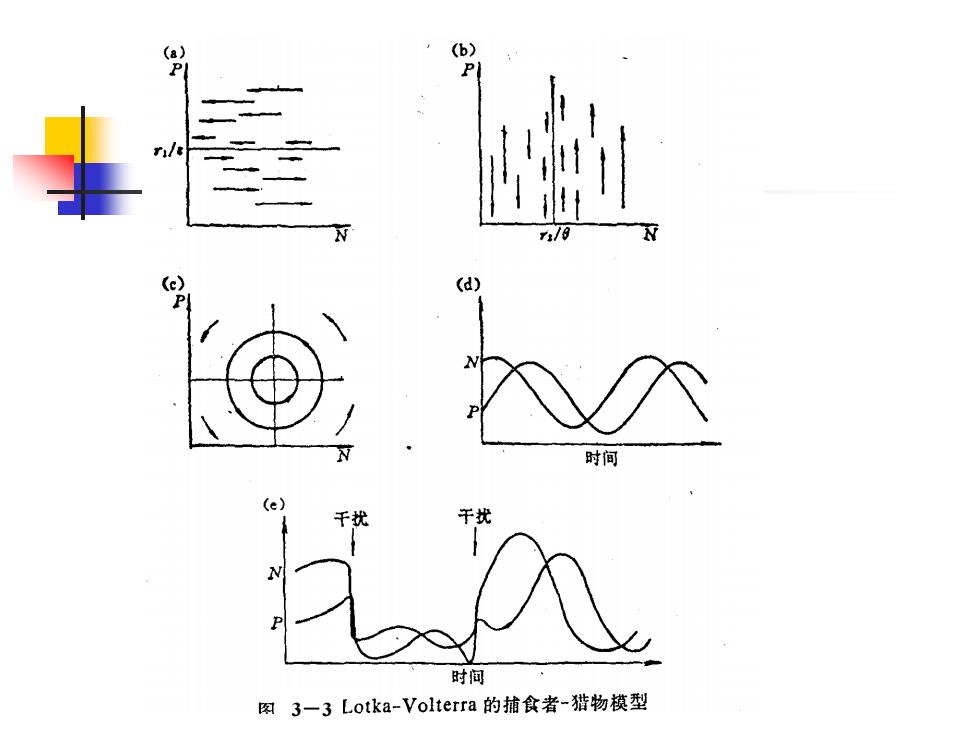
3-3
3-3

第二节 种间竞争和生态位理论 一、种间竞争 3-4
第二节 种间竞争和生态位理论 一、种间竞争 3-4

高斯假说(Gause’s hypothesis)或竞争排斥原理 (Principle of competitive exclusion),即亲缘关系接近的、 具有同样习性或生活方式的物种不可能长期在同一地区生 活,即完全的竞争者不能共存,因为它们的生态位没有差 别。 哈奇森(Hutchinson)指出,高斯假说有两个例外。 第一,由于环境因素强烈的作用(如天敌和不适宜气候及 食物关系),种群被抑制在一个低密度水平上。第二,因 环境不断地发生变动,竞争的结果不能达到一定的平衡 (即在能够充分利用环境的可能性之前,环境已经变化 了)。 (一)高斯假说
高斯假说(Gause’s hypothesis)或竞争排斥原理 (Principle of competitive exclusion),即亲缘关系接近的、 具有同样习性或生活方式的物种不可能长期在同一地区生 活,即完全的竞争者不能共存,因为它们的生态位没有差 别。 哈奇森(Hutchinson)指出,高斯假说有两个例外。 第一,由于环境因素强烈的作用(如天敌和不适宜气候及 食物关系),种群被抑制在一个低密度水平上。第二,因 环境不断地发生变动,竞争的结果不能达到一定的平衡 (即在能够充分利用环境的可能性之前,环境已经变化 了)。 (一)高斯假说

两个种群未出现竞争时: 两者出现竞争时: α和β分别表示物种甲和乙的竞争系数 dN1 dt =r1N1( K1-N1 K 1 ) dN2 dt =r2N2( K2-N2 K 2 ) dN1 dt =r1N1( K1-N1-αN2 K 1 ) dN2 dt =r2N2( K2-N2-βN1 K 2 ) ◼(二) Lotka-Volterra的种间竞争模型
两个种群未出现竞争时: 两者出现竞争时: α和β分别表示物种甲和乙的竞争系数 dN1 dt =r1N1( K1-N1 K 1 ) dN2 dt =r2N2( K2-N2 K 2 ) dN1 dt =r1N1( K1-N1-αN2 K 1 ) dN2 dt =r2N2( K2-N2-βN1 K 2 ) ◼(二) Lotka-Volterra的种间竞争模型