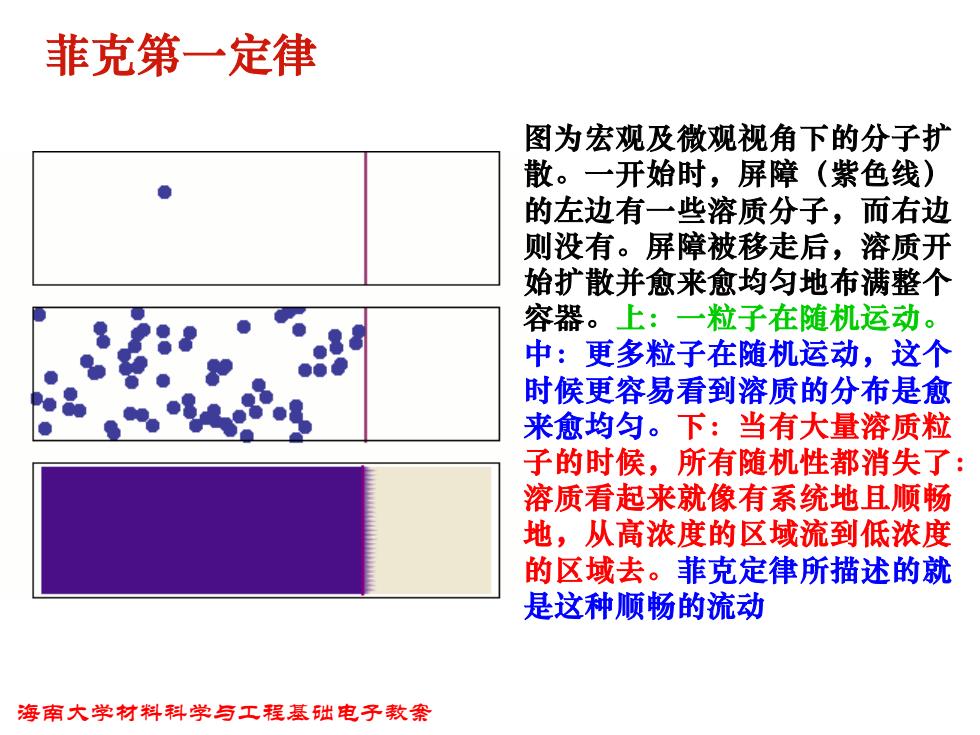
菲克第一定律 图为宏观及微观视角下的分子扩 散。一开始时,屏障(紫色线) 的左边有一些溶质分子,而右边 则没有。屏障被移走后,溶质开 始扩散并愈来愈均匀地布满整个 容器。上:一粒子在随机运动。 中:更多粒子在随机运动,这个 时候更容易看到溶质的分布是愈 来愈均匀。下:当有大量溶质粒 子的时候,所有随机性都消失了: 溶质看起来就像有系统地且顺畅 地,从高浓度的区域流到低浓度 的区域去。菲克定律所描述的就 是这种顺畅的流动 海南大学材料科学与工程基础电子教案
海南大学材料科学与工程基础电子教案 菲克第一定律 图为宏观及微观视角下的分子扩 散。一开始时,屏障(紫色线) 的左边有一些溶质分子,而右边 则没有。屏障被移走后,溶质开 始扩散并愈来愈均匀地布满整个 容器。上:一粒子在随机运动。 中:更多粒子在随机运动,这个 时候更容易看到溶质的分布是愈 来愈均匀。下:当有大量溶质粒 子的时候,所有随机性都消失了: 溶质看起来就像有系统地且顺畅 地,从高浓度的区域流到低浓度 的区域去。菲克定律所描述的就 是这种顺畅的流动

菲克第一定律 1858年,菲克(Fick)参照傅里叶(Fourier) 于1822年建立的导热方程,获得了描述物质从 高浓度区向低浓度区迁移的定量公式 假设有一单相固溶体,横截面积为A,浓度C不均匀,在d时 间内,沿x方向通过x处截面所迁移的物质的量与x处的浓度梯 成正比: △C △moc A△t △x dm =-D( 0 Adt 海南大学材料科学与工程基础电子教案
海南大学材料科学与工程基础电子教案 假设有一单相固溶体,横截面积为A,浓度C不均匀,在dt时 间内,沿x方向通过x处截面所迁移的物质的量与x处的浓度梯 成正比: A t x C m ( ) x C D Adt dm = − 菲克第一定律 1858年,菲克(Fick)参照傅里叶(Fourier) 于1822年建立的导热方程,获得了描述物质从 高浓度区向低浓度区迁移的定量公式

由扩散通量的定义,有 ac JJ-D (1) 8x 上式即菲克第一定律宏观表达式。 式中J称为扩散通量,是单位时间内通过垂直于x轴的单 位面积的原子数量,常用单位是g/(cm2.s)或mol/(cm2.s); D是比例系数,指是同一时刻沿轴的浓度梯度,称为扩 散系数,是单位浓度梯度下的扩散通量,单位为cm/s或m/s; 负号表示扩散方向与浓度梯度方向相反
上式即菲克第一定律宏观表达式。 式中J称为扩散通量,是单位时间内通过垂直于x轴的单 位面积的原子数量,常用单位是g/(cm2 .s)或mol/(cm2 .s) ; D是比例系数,指是同一时刻沿轴的浓度梯度,称为扩 散系数,是单位浓度梯度下的扩散通量,单位为cm2 /s或m2 /s; 负号表示扩散方向与浓度梯度方向相反 x C J D = − 由扩散通量的定义,有 (1)
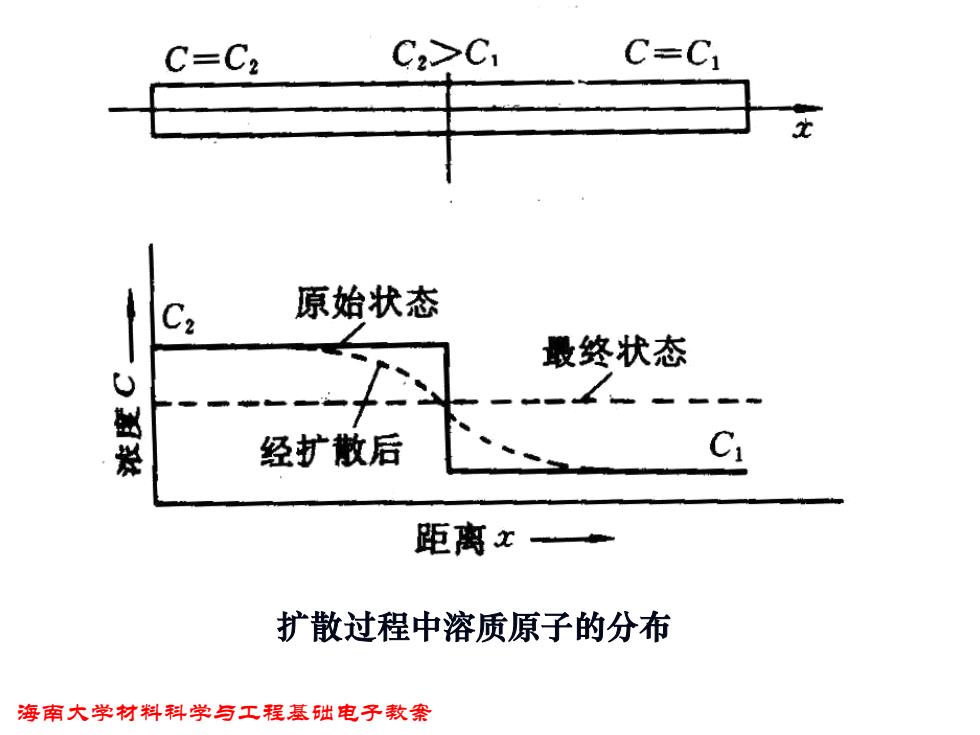
C=C2 C2>C1 C=C C2 原始状态 最终状态 茶 经扩散后 Ci 距离x 扩散过程中溶质原子的分布 海南大学材料科学与工程基础电子教案
海南大学材料科学与工程基础电子教案 扩散过程中溶质原子的分布
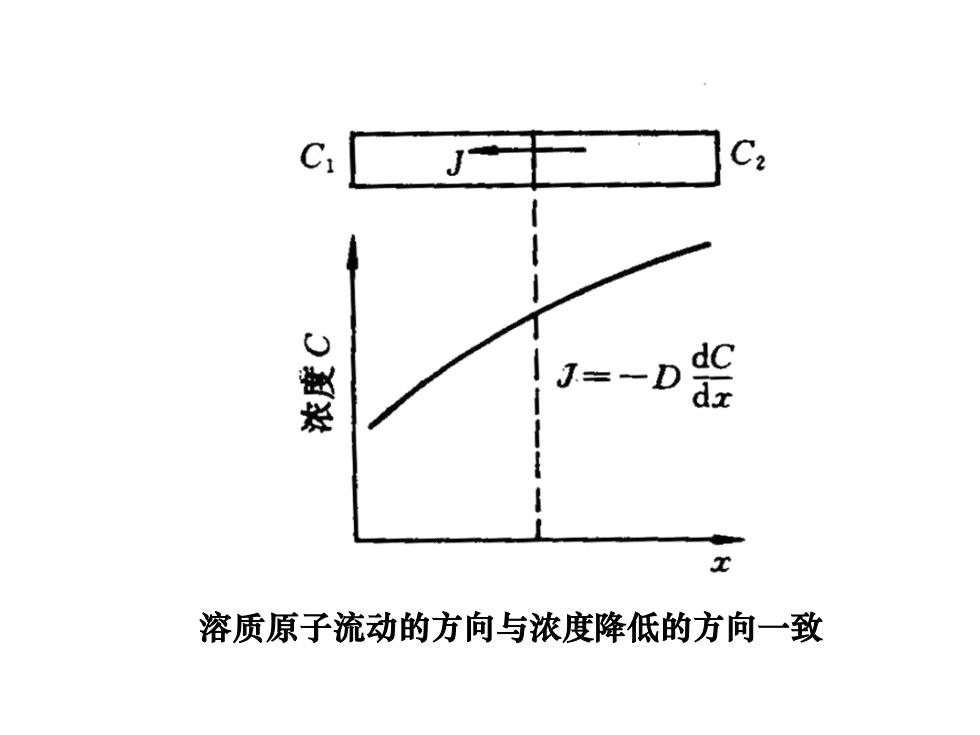
J=-D x 溶质原子流动的方向与浓度降低的方向一致
溶质原子流动的方向与浓度降低的方向一致