
省领精品课程一材料力学 此式表明,沿腹板高度,剪应力也是按二次抛物线分布的,如图8-8(b)所示。 t品Bm-B-bm tw 由于B》b,故x与x很接近,因此腹板上的剪应力大致上均匀分布。结果表明,腹 板承担了95以上的剪力。因此,作为近似计算,工字型截面梁的最大剪应 品 (8-10) 工字型截面翼缘的剪应力将在8-5中时论 T市加立 图8-9 三、圆形及薄壁圆坏截面梁 由剪应力互等定理知,圆形截面边缘上各点的剪应力必与圆周相切,因而,一般来说剪 应力π的方向与剪力Q不平行,故对矩形截面剪应力方向的假定在这里已不适用(图8-10) 但可以证明,最大的应力x仍发牛在中性轴上,日中性轴上名点剪应力可以认为话合前面 对矩形截面所作的假定(图8-10)。因此可以应用公式(8-8)来计算圆形截面的最大剪应 心受兴品,背 代入(8-8)式得 4040 3743 (8-11) This document is generated by trial version of Print2Flash(www.printflash.com)
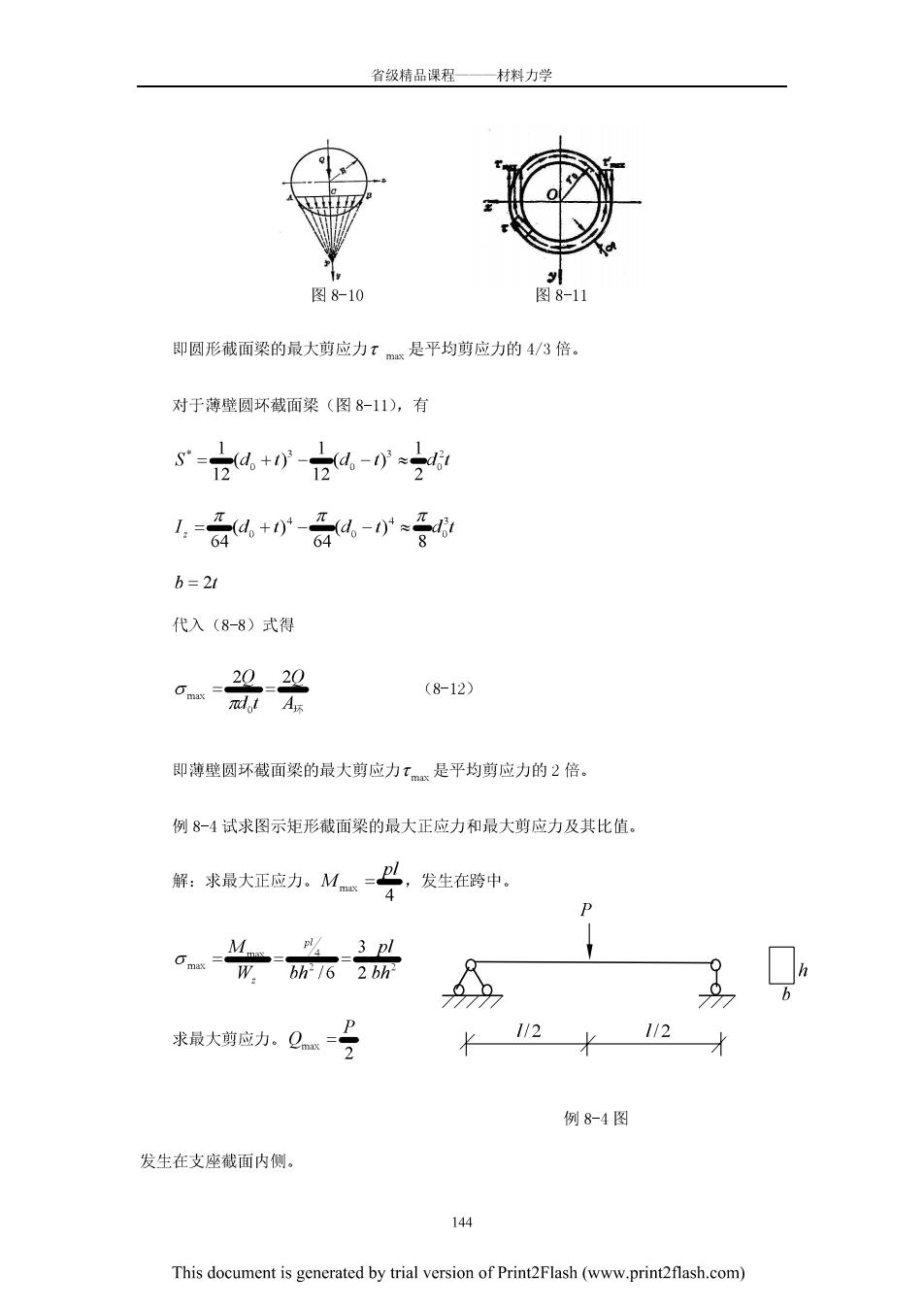
省领精品课程—材料力学 图8-10 即圆形截面梁的最大剪应力是平均剪应力的4/3倍 对于薄壁圆环截面梁(图8-1山),有 =z4+W-*2 1,=哥4+0-少*受 b=21 代入(8-8)式得 。部头 (8-12) 即薄壁圆环截面梁的最大剪应力是平均剪应力的2倍。 例8-4试求图示矩形截面梁的最大正应力和最大剪应力及其比值。 解:求最大正应力。M一,发生在跨中 P 3 pl om-W7元62所 求最大期应力:Q号 12米 112 例8-4图 发生在支座截面内侧。 14 This document is generated by trial version of Print2Flash(www.print2flash.com)

省级桔品课程 一材料力学 0治 最大应力的比值是 。为 工程的大多数梁,I远大于,因而Gs远大于t,即弯曲正应力常常是控制因素. §8.4同时考虑正应力和剪应力时梁的强度计算 由上一节的分析知道,染的最大剪应力发生在中性轴上,而中性轴上各点的正应力为零 因此中性轴上的点是纯剪切应力状态,故与杆在扭转时的强度条件类似,按最大工作剪应力 Tm来建立梁的剪应力强度条件: tar≤[r] (8-13) 对梁进行强度计算时,应同时考虑正应力强度条件(8-7)和剪应力强度条件(813)。 我们前面说过,梁的主要变形是弯曲变形。因此,一般情况下先按正应力强度条件讲行福度 计算,如设计载面或确定容许载荷或强度 交核,然后校校剪应力强度。但在下列情况下,剪 应力强度必须予以充分注意:(1)梁的跨度较短,或者在支座附近有较大的载荷,因而梁的 弯矩较小而剪力较大:(2)铆接或焊接的组合截面梁,当腹板的厚度与高度之比小于型钢的 相应比值,也就是腹板既薄又高时,此时腹板的剪应力可能很大:(3)木材的顺纸抗剪强度 低。还有些梁是由几部分胶合、焊接或柳接而成,对这些梁要考虑纵截面上的剪切。 例8-5试校核例8-1松木梁的剪应力强度,已知松木的抗剪容许应力[]=0.9Wp阳 解:由剪应力互等定理,纵截面和横截面上剪应力相等 3Q. 36×103×2.4/2 Tms=2A=2120x180×10 =0.5Mpa tm<[x],故安全 例8-6试校核例8-2所选择截面梁的剪应力强度,己知材料的容许剪应力[π]=100州p阳 解:QP, 圆藏面,【m-3A3044×10 40425×103 =2.05MPa 矩形截面,s 30-30-325x10 262右2761x1522x10-324Pa 145 This document is generated by trial version of Print2Flash(www.printflash.com)