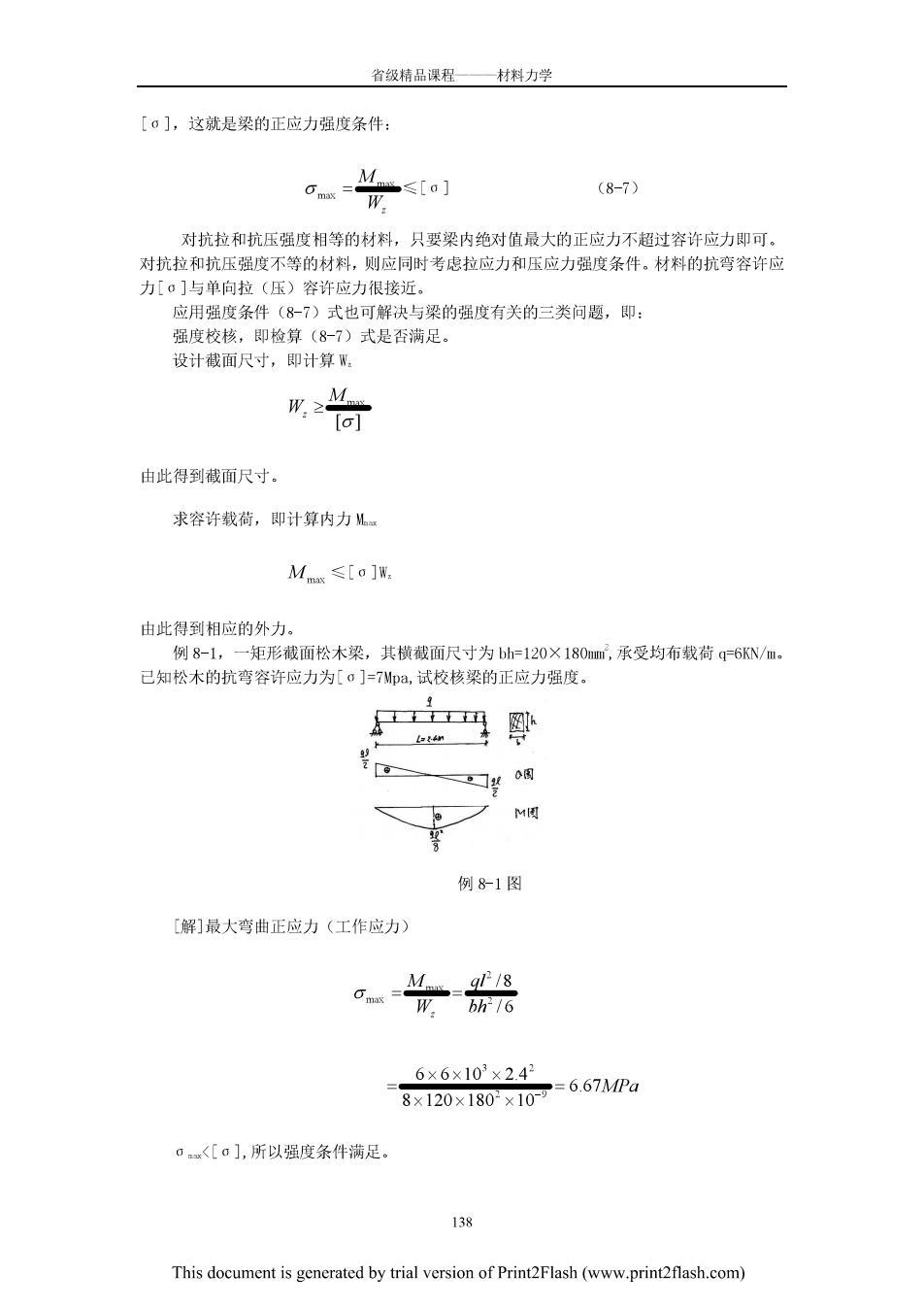
省级精品课程—材料力学 【。],这就是梁的正应力强度条件: (8-7) 对抗拉和抗压强度相等的材料,只要梁内绝对值最大的正应力不超过容许应力即可 对抗拉和抗压强度不等的材料,则应同时考虑拉应力和压应力强度条件。材料的抗弯容许应 力[·]与单向拉(压)容许应力很接近。 应用强度条件(87)式也可解决与梁的强度有关的三类问题,即: 强度校核,即检算(87)式是否满足。 设计截面尺寸,即计算 简 由此得到截面尺寸。 求容许载荷,即计算内力儿 Mm≤[o]W 由此得到相应的外力 例8-1,一矩形被面松木梁,其横藏面尺寸为bh-120×180m,承受均布载荷q6N/m, 已知松木的抗弯容许应力为[a]=7Mpa,试校核梁的正应力强度. M因 例81图 解]最大弯曲正应力(工作应力 6×6×103×2.4 8x120x180-x10=6.67MPa ·<[0],所以强度条件满足。 This document is generated by trial version of Print2Flash(www.print2flash.com)
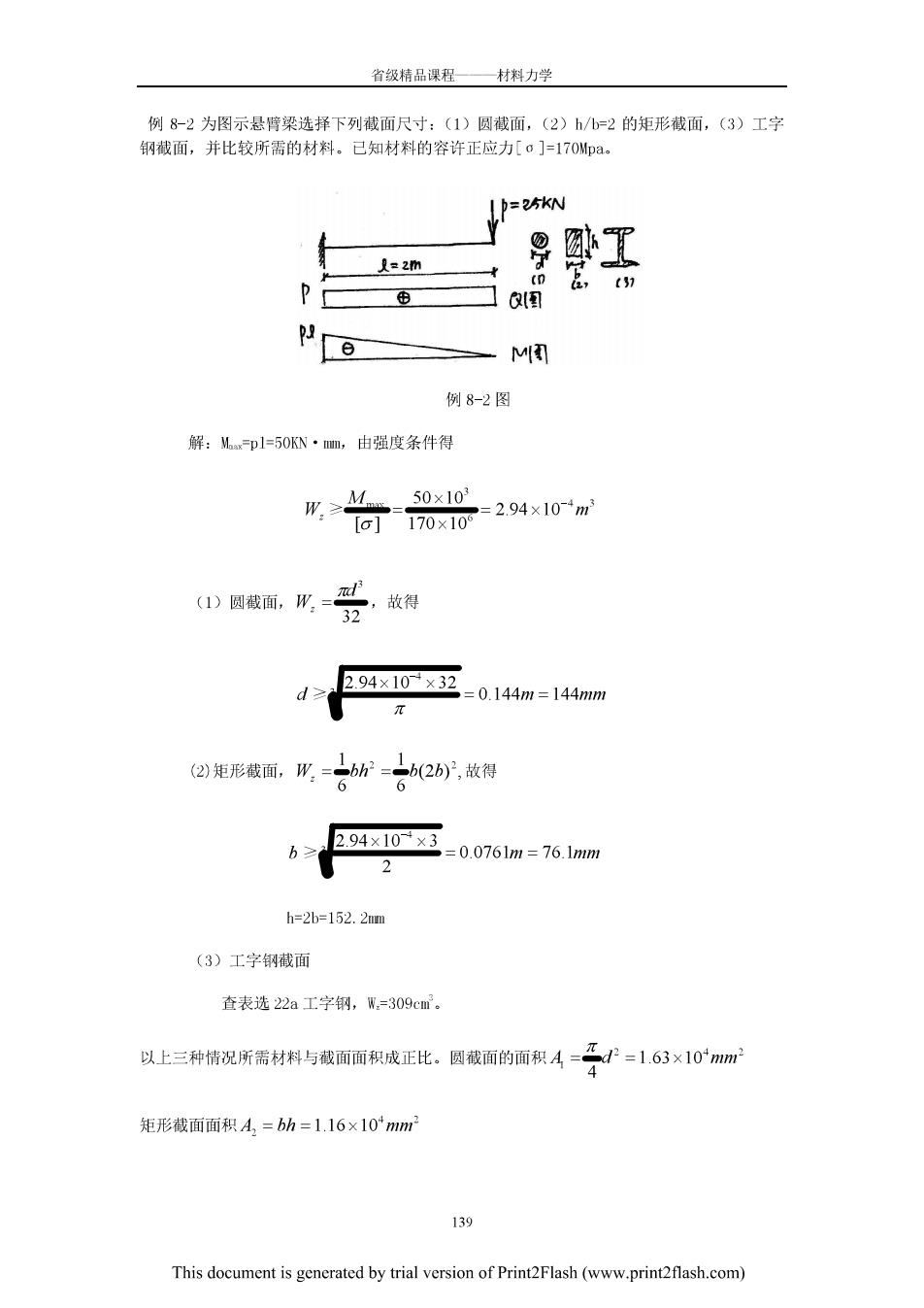
省领精品课程 一材料力学 例8-2为图示悬臂染选择下列藏面尺寸:(1)圆被面,(2)h/b=2的矩形截面,(3)工字 钢截面,并比较所需的材料.已知材料的容许正应力[o]=170Mpa. T 1=2m P 0图 T 例8-2图 解:cpl=50KN·m,由强度条件得 可770x10=294×10m 50×10° 医碳属,化 ,故得 d 294x10x32=0.144m=144mm (②)矩形截面,W=。bhb(2b,故得 b 294x10x3=0.0761m=76.1mm 2 h=2b=152.2m (3)工字钢截面 查表选22a工字钢,黑=309cm。 以上三种情况所需材料与截面面积成正比。圆截面的面积A=二=1.63×10mm 矩形截面面积A,=bh=116×10mm 139 This document is generated by trial version of Print2Flash(www.printflash.com)

省级精品课程—材料力学 查表得工字钢截面积A,=0.42×10mm 其比值为A:A:A=1:0.712:0.258 由此可见,从满足弯曲正应力强度条件来看,工字钢截面最省料,矩形截面次之,圆 截面最差 §8.3弯曲剪应力 梁在横力弯曲时,其横截面上除了弯矩外,还有剪力,相应地就有剪应力。本节将分析 几种被面形状梁的剪应力,与前面的正应力分析一样,仍限于研究外力作用在梁的纵向对称 面的情况。 ·、矩形截哉面级 设矩形藏面的高为h宽为b,截面上的剪力Q沿截面的纵对称轴y作用。(图8-6b)注 意到梁的侧面是自由表面,由剪应力互等定理知,横面侧边上各点的剪应力方向都平行于 侧边。对于狭长的矩形截面来说,可以认为剪应力的大小和方向沿截面宽度的变化不大。因 此,可以对矩形截裁面剪应力的分布规律作如下假定: (1)横截面上各点剪应力的方向都平行于侧边,也即平行于剪力Q: (2)沿战面的☆度道应力均匀分布 进一步研究表明, 以上述假定为基础的解与精确解相比有足够的准确度, 现在研究剪应力的大小沿高度的变化规律。 ws证 图8-6 用截面1-1和2-2取出一长为x的微段梁,为简单起见,设微段梁两截面上的剪力Q相等 而弯矩却不同,见图8-6(a)和(c)。弹性理论的分析表明,对于剪力Q沿梁长变化的情况, 用这个简化方法得到的结果也是足够精确的。与剪力和弯矩对应地在两面上有正应力 剪应力t,见图8-6(d)。但用这一段柴仍无法说明剪应力t沿高度的分布问题,为此,在 距中性轴为y处,用平行于中性层的平面3-3将做段梁切开,取下部一小块来分析:小块的 左右侧面上有正应力和剪应力x,根据剪应力互等定理,它等于横藏面上距中性轴为y处的 140 This document is gencrated by trial version of Print2Flash(www.print2flash.com)

省领精品课程一材料力学 剪应力,见图86()和()。研究小块在x方向的平衡条件,计算小块侧面和顶面上内力 的合力 N-ja=1兰4兰 a=a T=7'bdx=t bdx 由平衡条件ΣX=0,即NN-T=0 ÷0 红起0兴:究 (8-8) 这就是矩形截面矩中性轴为y处的剪应力公式。要特别注意式中S是距中性轴为y的横线以 外的部分横截面面积A对中性轴的面积矩,它是一个变量,随着距离y而改变。如图8-7 新示 图8-7 修冷归共 o h 以: -74-y) 14 This document is generated by trial version of Print2Flash(www.printflash.com)

省领精品课程—材料力学 由此可见。剪应力的大小沿矩形鞍面的高度二次抛物线规律变化。在上下边峰y=士分》处 =0:在中性轴上(y=0)剪应力达到最大值: 受 代A1,管得 品兴 (8-9) 即矩形截面的最大剪应力是平均剪应力的3/2倍。 二、工字型截面梁及其他组合矩形藏面梁 图8-8 工字型截面由腹板和冀缘两部分组成(图&-8)。由于腹板是狭长矩形,故仍可用公式 (8-8)来计算剪应力。 此时b为腹板的宽度,S为图中8-8中阴影线部分的面积对中性轴的面积矩 S=B号号+分+空-停+分 是H-)+-4) 于是 tW-)+-4 This document is gencrated by trial version of Print2Flash (www.print2flash.com)