
大连理工大学博士学位论文 机器鱼的摆动控制方程。分别采用近似方法推导合金薄板在均匀分布、非均匀分布以及 考虑超磁材料的均匀和非均匀分布下的层合悬臂梁的固有频率和固有振型。 (2)推导线性控制方程及其求解方法,给出鱼游动驱动力和游动方程。对超磁材料 仿生机器鱼模型设定计算参数,分析超磁仿生机器鱼游动位移与外磁场频率的关系、超 磁仿生机器鱼沿体长的驱动力分布以及机器鱼游动特征与轨迹等。分析尾涡推力的作 用,对外磁场采用变频率控制的方法对游动状况进行模拟。 (3)考虑仿生机器鱼在非线性阻尼和几何大变形情况下的摆动控制方程,并对方程 进行求解。然后分析其简化的驱动力表达式,选取适当的机器鱼材料和几何参数,对简 单算例采用数值方法计算,得到数值模拟结果。采用肌电图形式的外磁场模仿典型鱼类 巡航和起动时的肌电图,得到仿生模拟结果。 (4)推导仿生机器鱼参数优化的数值计算模型,对仿生机器鱼的仿生骨架和肌肉的 厚度进行参数优化。通过计算优化出较好的厚度分布方式,并给出这种情况下的超磁材 料仿生机器鱼游动特点、鱼体运动特点以及机器鱼游动轨迹等。 (⑤)考虑附加惯性效应,推导仿生机器鱼游动时的控制方程,采用近似平均的方法 对方程进行线性化后用分离变量法求解,接着计算游动距离与外磁场频率的关系曲线, 以及在几个外磁场频率下游动驱动力、游动距离、游动速度和游动轨迹等随时间的变化 曲线。 -13- 万方数据
大连理工大学博士学位论文 机器鱼的摆动控制方程。分别采用近似方法推导合金薄板在均匀分布、非均匀分布以及 考虑超磁材料的均匀和非均匀分布下的层合悬臂梁的固有频率和固有振型。 (2)推导线性控制方程及其求解方法,给出鱼游动驱动力和游动方程。对超磁材料 仿生机器鱼模型设定计算参数,分析超磁仿生机器鱼游动位移与外磁场频率的关系、超 磁仿生机器鱼沿体长的驱动力分布以及机器鱼游动特征与轨迹等。分析尾涡推力的作 用,对外磁场采用变频率控制的方法对游动状况进行模拟。 (3)考虑仿生机器鱼在非线性阻尼和几何大变形情况下的摆动控制方程,并对方程 进行求解。然后分析其简化的驱动力表达式,选取适当的机器鱼材料和几何参数,对简 单算例采用数值方法计算,得到数值模拟结果。采用肌电图形式的外磁场模仿典型鱼类 巡航和起动时的肌电图,得到仿生模拟结果。 (4)推导仿生机器鱼参数优化的数值计算模型,对仿生机器鱼的仿生骨架和肌肉的 厚度进行参数优化。通过计算优化出较好的厚度分布方式,并给出这种情况下的超磁材 料仿生机器鱼游动特点、鱼体运动特点以及机器鱼游动轨迹等。 (5)考虑附加惯性效应,推导仿生机器鱼游动时的控制方程,采用近似平均的方法 对方程进行线性化后用分离变量法求解,接着计算游动距离与外磁场频率的关系曲线, 以及在几个外磁场频率下游动驱动力、游动距离、游动速度和游动轨迹等随时间的变化 曲线。 万方数据

超磁仿生机器鱼力学机理及数值模拟 2超磁致伸缩材料仿生机器鱼的简化模型 本章首先介绍了超磁致伸缩材料的力学性能,然后将鱼尾摆动简化成悬臂板的振动 模型。假设鱼尾骨架用合金薄板模拟,鱼尾肌肉用超磁致伸缩材料模拟,鱼的神经控制 系统用外磁场模拟。解释了在外磁场作用下磁致伸缩材料对板的载荷作用。给出了超磁 机器鱼在几种情况下的固有频率和固有振型的求解过程。 2.1超磁致伸缩材料力学性能 超磁致伸缩材料是近年发展起来的新型功能材料,它有极大的磁致伸缩系数值。这 里简要介绍它的磁致伸缩效应和主要工作特性。 (1)磁致伸缩效应 磁致伸缩效应一般可分为两种形式:线磁致伸缩和体磁致伸缩。超磁材料在磁化过 程中沿磁化方向有线度的伸长或缩短,称为线磁致伸缩2,如图2.1所示。通常用1来 表示线磁致伸缩系数,其表达式为: 2=△1/1o, (2.1) 其中,1。为超磁材料的初始长度,△1为超磁材料在长度方向上的变化量。1的符号可正 可负,当入>0时,表示超磁材料沿磁场方向伸长,而垂直于磁场方向缩短,它为正线 磁致伸缩:当入<0时,表示沿磁场方向缩短,垂直于磁场方向伸长,它为负线磁致伸 缩。 图2.1超磁材料体的线磁致伸缩示意图 Fig.2.1 Linear magnetostrictive sketch of the GMM body -14- 万方数据
超磁仿生机器鱼力学机理及数值模拟 2超磁致伸缩材料仿生机器鱼的简化模型 本章首先介绍了超磁致伸缩材料的力学性能,然后将鱼尾摆动简化成悬臂板的振动 模型。假设鱼尾骨架用合金薄板模拟,鱼尾肌肉用超磁致伸缩材料模拟,鱼的神经控制 系统用外磁场模拟。解释了在外磁场作用下磁致伸缩材料对板的载荷作用。给出了超磁 机器鱼在几种情况下的固有频率和固有振型的求解过程。 2.1 超磁致伸缩材料力学性能 超磁致伸缩材料是近年发展起来的新型功能材料,它有极大的磁致伸缩系数值。这 里简要介绍它的磁致伸缩效应和主要工作特性。 (1)磁致伸缩效应 磁致伸缩效应一般可分为两种形式:线磁致伸缩和体磁致伸缩。超磁材料在磁化过 程中沿磁化方向有线度的伸长或缩短,称为线磁致伸缩【1021,如图2.1所示。通常用允来 表示线磁致伸缩系数,其表达式为: 五=AI/乇, (2.1) 其中,,n为超磁材料的初始长度,出为超磁材料在长度方向上的变化量。旯的符号可正 可负,当允>0时,表示超磁材料沿磁场方向伸长,而垂直于磁场方向缩短,它为正线 磁致伸缩;当五<0时,表示沿磁场方向缩短,垂直于磁场方向伸长,它为负线磁致伸 缩。 图2.1超磁材料体的线磁致伸缩示意图 Fig.2.1 Linear magnetostrictive sketch of the GMM body 一14 万方数据

大连理工大学博士学位论文 体磁致伸缩是超磁材料在磁化过程中发生体积膨胀或收缩。体磁致伸缩主要发生在 磁化饱和以后。体磁致伸缩系数用®表示,表达式为: o=△V/V, (2.2) 其中,V为超磁材料的原始体积,△V为磁化后的超磁材料的体积变化量。当o>0时, 它表示超磁材料在磁化过程中发生膨胀,为正体磁致伸缩:当0<0时,表示超磁材料 在磁化过程中发生收缩,为负体磁致伸缩031。 超磁材料的体磁致伸缩通常很小,大量的研究和应用主要是在线磁致伸缩领域,所 以磁致伸缩常指线磁致伸缩1)。 (2)主要工作特性o21 超磁致伸缩材料具有磁性和弹性双重性质,在外磁场作用下,其内部会产生应力σ 和应变ε。其中,所产生的应变由两部分组成:一部分为磁致伸缩引起的应变,用ε:表 示: En=dH, (2.3) 式中,d为动态磁致伸缩系数d= OA ,H为外部磁场强度:另一部分为应力作用 OH =const 引起的应变,用ε。表示: 6,=Sg, (2.4) 式中,SH为柔顺系数S"= ,σ为应力。应变ε和应力σ与外部磁场强度以及 88H-const 磁感应强度满足的超磁致伸缩材料的本构关系可表示为: 8=e。+eH=SHσ+dH, (2.5) B=d'o+°H, (2.6) 其中,£为总应变,d”为逆动态磁致伸缩系数,μ°磁导率,B为磁感应强度12。 稀土超磁致伸缩材料的弹性模量E会随着外磁场而变化,其变化曲线如图22所示。 当超磁致伸缩材料达到磁化饱和后,由磁致伸缩引起的长度变化就不再发生,这时的弹 性模量将不受磁场的影响。 -15- 万方数据
大连理工大学博士学位论文 体磁致伸缩是超磁材料在磁化过程中发生体积膨胀或收缩。体磁致伸缩主要发生在 磁化饱和以后。体磁致伸缩系数用缈表示,表达式为: 缈=AVIV, (2.2) 其中,y为超磁材料的原始体积,AV为磁化后的超磁材料的体积变化量。当国>0时, 它表示超磁材料在磁化过程中发生膨胀,为正体磁致伸缩;当缈<0时,表示超磁材料 在磁化过程中发生收缩,为负体磁致伸缩‘1031。 超磁材料的体磁致伸缩通常很小,大量的研究和应用主要是在线磁致伸缩领域,所 以磁致伸缩常指线磁致伸缩‘1031。 (2)主要工作特性‘102】 超磁致伸缩材料具有磁性和弹性双重性质,在外磁场作用下,其内部会产生应力O- 和应变占。其中,所产生的应变由两部分组成:一部分为磁致伸缩引起的应变,用sH表 不: sH=dH, (2.3) 式中,d为动态磁致伸缩系数d=筹L:。。啦,H为外部磁场强度;另一部分为应力作用 引起的应变,用s。表示: %=S爿仃, (2.4) 式中, SⅣ为柔顺系数sH:尝l ,仃为应力。应变s和应力仃与外部磁场强度以及 a仃In:conn 磁感应强度满足的超磁致伸缩材料的本构关系可表示为: s=乞+%=S爿盯+dH, (2.5) B=d'o-+/x盯H, (2.6) 其中,s为总应变,d’为逆动态磁致伸缩系数,∥。磁导率,曰为磁感应强度‘1021。 稀土超磁致伸缩材料的弹性模量E会随着外磁场而变化,其变化曲线如图2.2所示。 当超磁致伸缩材料达到磁化饱和后,由磁致伸缩引起的长度变化就不再发生,这时的弹 性模量将不受磁场的影响。 万方数据
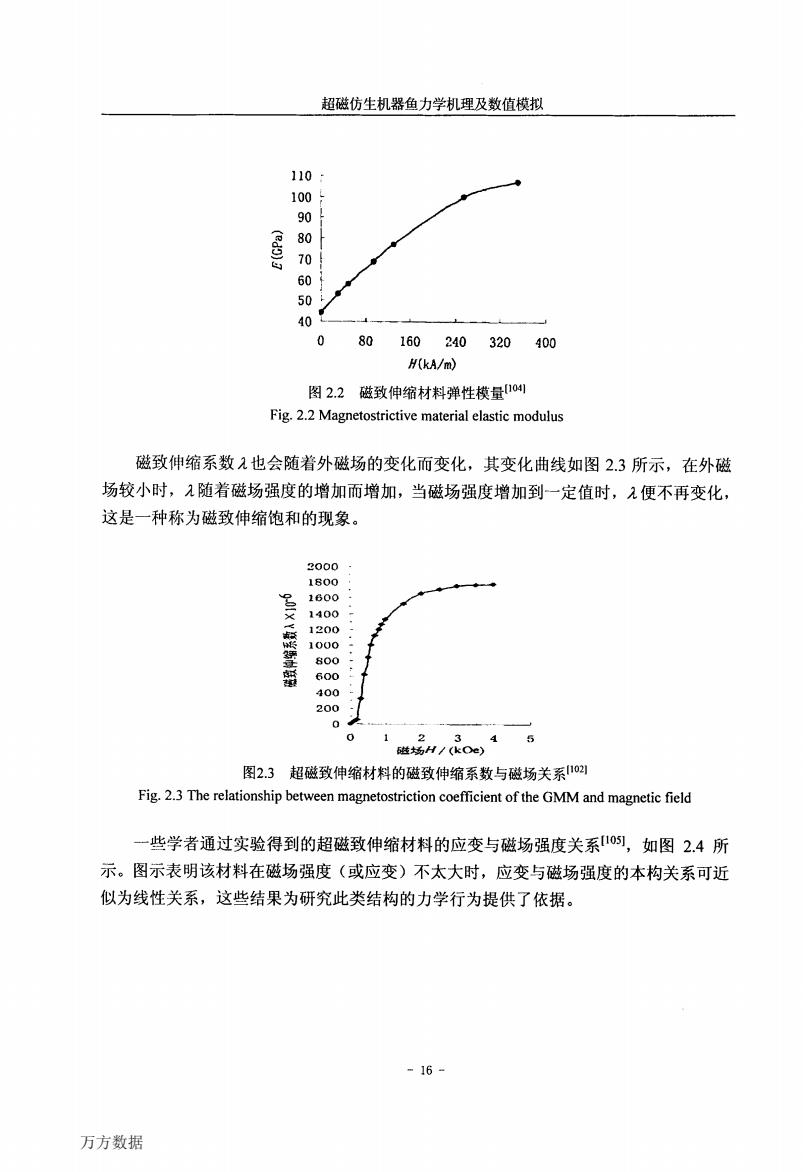
超磁仿生机器鱼力学机理及数值模拟 110 100 90 80 60 50 40 0 80 160240 320 400 H(kA/m) 图22磁致伸缩材料弹性模量04, Fig.2.2 Magnetostrictive material elastic modulus 磁致伸缩系数入也会随着外磁场的变化而变化,其变化曲线如图2.3所示,在外磁 场较小时,1随着磁场强度的增加而增加,当磁场强度增加到一定值时,2便不再变化, 这是一种称为磁致伸缩饱和的现象。 2000 1800 1600 1400 1200 1000 800 蟹 600 400 200 0 12345 磁场H/(kOe) 图2.3超磁致伸缩材料的磁致伸缩系数与磁场关系叫 Fig.2.3 The relationship between magnetostriction coefficient of the GMM and magnetic field 一些学者通过实验得到的超磁致伸缩材料的应变与磁场强度关系1),如图2.4所 示。图示表明该材料在磁场强度(或应变)不太大时,应变与磁场强度的本构关系可近 似为线性关系,这些结果为研究此类结构的力学行为提供了依据。 -16- 万方数据
超磁仿生机器鱼力学机理及数值模拟 l 10 100 90 趸80 蓄70 60 50 40。——一—I~一—-—————L_————-二—————1 0 80 160 240 320 400 Ⅳ(从/m) 图2.2磁致伸缩材料弹性模量【1041 Fig.2.2 Magnetostrictive material elastic modulus 磁致伸缩系数允也会随着外磁场的变化而变化,其变化曲线如图2.3所示,在外磁 场较小时,川箍着磁场强度的增加而增加,当磁场强度增加到一定值时,见便不再变化, 这是一种称为磁致伸缩饱和的现象。 岬 × 碡薹 懵终 静曩潞翘 磁场Ⅳ/(kOe) 图2.3超磁致伸缩材料的磁致伸缩系数与磁场关系‘1021 Fig.2.3 The relationship between magnetostriction coefficient ofthe GMM and magnetic field 一些学者通过实验得到的超磁致伸缩材料的应变与磁场强度关系【1051,如图2.4所 示。图示表明该材料在磁场强度(或应变)不太大时,应变与磁场强度的本构关系可近 似为线性关系,这些结果为研究此类结构的力学行为提供了依据。 万方数据
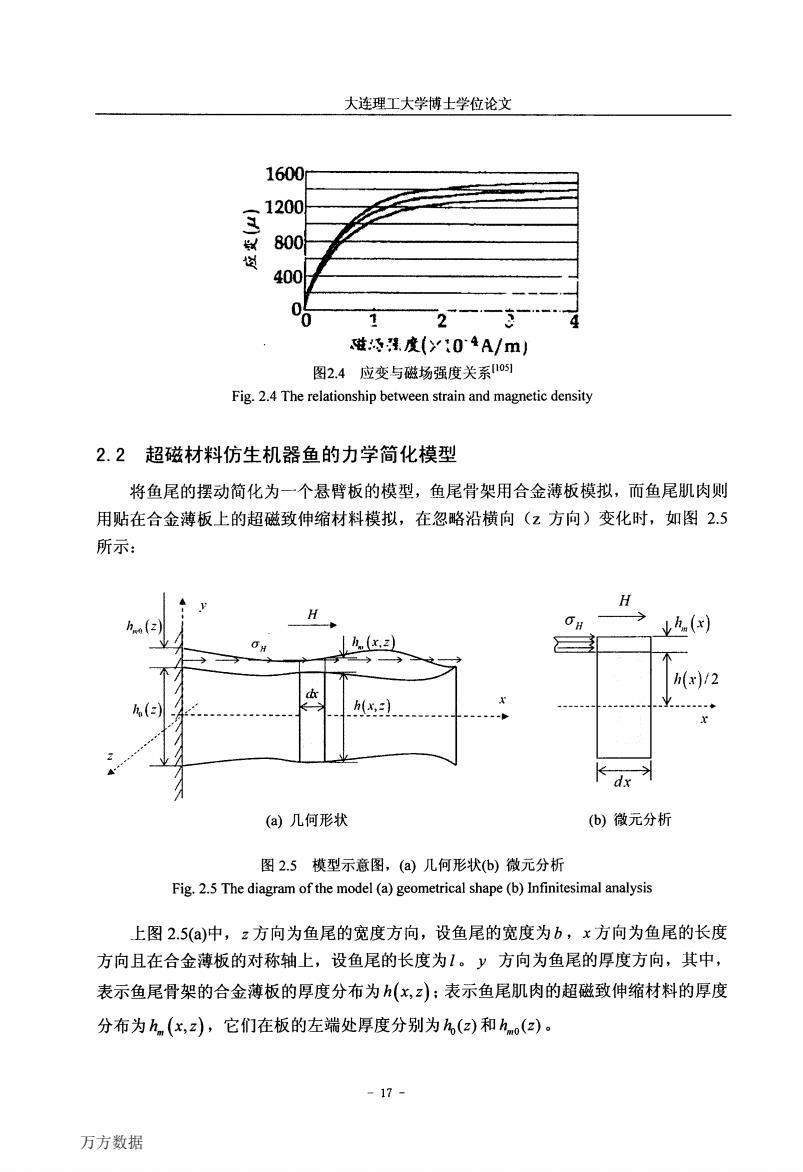
大连理工大学博士学位论文 1600 1200 800 400 磁程.度04A/m) 图2.4应变与磁场强度关系1o1 Fig.2.4 The relationship between strain and magnetic density 2.2超磁材料仿生机器鱼的力学简化模型 将鱼尾的摆动简化为一个悬臂板的模型,鱼尾骨架用合金薄板模拟,而鱼尾肌肉则 用贴在合金薄板上的超磁致伸缩材料模拟,在忽略沿横向(z方向)变化时,如图2.5 所示: H H th(x) h(x.2 不 h(x)/2 hsl -D dx (a)几何形状 (b)微元分析 图2.5模型示意图,(a)几何形状(b)微元分析 Fig.2.5 The diagram of the model (a)geometrical shape(b)Infinitesimal analysis 上图2.5(a)中,z方向为鱼尾的宽度方向,设鱼尾的宽度为b,x方向为鱼尾的长度 方向且在合金薄板的对称轴上,设鱼尾的长度为1。y方向为鱼尾的厚度方向,其中, 表示鱼尾骨架的合金薄板的厚度分布为h(x,z):表示鱼尾肌肉的超磁致伸缩材料的厚度 分布为h,(x,z),它们在板的左端处厚度分别为h,(z)和h(z)。 -17- 万方数据
大连理工大学博士学位论文 160a ,.、1200 ≮ 留800 嗵 400 _●·__·---_-·--_-__一 .1 帆·---_·●‘,_…一· 2 0 磁糟冀。度《>7:O‘4a/mj 图2.4应变与磁场强度关系【1051 Fig.2.4 The relationship between strain and magnetic density 2.2超磁材料仿生机器鱼的力学简化模型 将鱼尾的摆动简化为一个悬臂板的模型,鱼尾骨架用合金薄板模拟,而鱼尾肌肉则 用贴在合金薄板上的超磁致伸缩材料模拟,在忽略沿横向(z方向)变化时,如图2.5 所示: ‰ , ./ 。/’ K J ‘Jj H ’z) ■ 、 r f。 r『 h fr z1 / , J、 、f f f :汴=争:乏 dr 菇瓢写 ’二) f / \ / 、 , 办(工,:) , 乃 /’ } 、 f Jf } ‘ (a)几何形状 玑. 7驴m / 卜 tl( 、 r (b)微元分析 图2.5模型示意图,(a)几何形状(b)微元分析 Fig.2.5 The diagram of the model(a)geometrical shape(b)Infinitesimal analysis 上图2.5(a)中,2方向为鱼尾的宽度方向,设鱼尾的宽度为b,工方向为鱼尾的长度 方向且在合金薄板的对称轴上,设鱼尾的长度为,。Y方向为鱼尾的厚度方向,其中, 表示鱼尾骨架的合金薄板的厚度分布为h(x,z);表示鱼尾肌肉的超磁致伸缩材料的厚度 分布为‰(x,z),它们在板的左端处厚度分别为ho(z)和k。(z)。 —J4 万方数据