
第11卷第5期 智能系统学报 Vol.11 No.5 2016年10月 CAAI Transactions on Intelligent Systems 0ct.2016 D0I:10.11992/6is.201508015 网络出版地址:http://www.cnki.net/kcms/detail,/23.1538.TP.20160824.0928.002.html 堆叠隐空间模糊C回归算法及其在 发酵数据多模型建模中的应用 刘欢,王骏,邓赵红,王士同 (江南大学数字蝶体学院,江苏无锡214122)》 摘要:切换回归算法FCR的性能容易受到噪声点以及离群点的影响,同时该算法对于复杂数据的处理能力较差。 对此,文中提出一种基于堆叠隐空间的模糊C回归算法。该算法将基于LM特征映射技术,利用主成分分析进行特 征提取,再结合多层前馈神经网络学习结构对隐空间进行多次扩展和压缩。实验结果表明,该算法具有更好的抗噪 性能,对模糊指数的变化不敏感,同时在处理复杂数据以及在多模型建模中更加精确、高效、稳定。 关键词:隐空间映射:极限学习机;主成分分析;模糊C回归算法:多层神经网络:多模型建模 中图分类号:TP181文献标志码:A文章编号:1673-4785(2016)05-0670-10 中文引用格式:刘欢,王骏,邓赵红,等堆叠隐空间模糊C回归算法及其在发酵数据多模型建模中的应用[J].智能系统学报,2016, 11(5):670-679. 英文写引用格式:LIU Huan,WANGJun,DENG Zhaohong,etal.A cascaded hidden space fuz四yC-regression algorithm and its ap- plication in multi-model modeling for the fermentation process [J].CAAI transactions on intelligent systems,2016,11(5):670-679. A cascaded hidden space fuzzy C-regression algorithm and its application in multi-model modeling for the fermentation process LIU Huan,WANG Jun,DENG Zhaohong,WANG Shitong School of Digital Media,JiangNan University,WuXi 214122,China) Abstract:The switching regression algorithm FCR is sensitive to noise data and outliers.The algorithm also has low levels of capability for dealing with complex data.In order to handle these problems,an improved fuzzy C-regres- sion algorithm is proposed based on cascaded hidden space.In our method,principal component analysis is com- bined with extreme machine learning feature mapping and multilayer feedforward neural networks.The experimental results show that our proposed method is more stable as regards noise data and outliers,and thus more suitable for handling complex data and multi-model modeling problems for the fermentation process. Keywords:hidden space feature mapping;extreme learning machine;principal component analysis;fuzzy C-re- gression algorithm;multilayer neural network;multi-model modeling. 切换回归模型在经济、数据挖掘等领域中有着 gression algorithm,FCR)算法,从而实现了对多个模 广泛的应用。近年来,基于模糊聚类分析4]的切 型的切换回归:在此基础上,文献[6]结合牛顿万有 换回归技术得到了广泛的研究。如文献[5]在模糊 引力定律提出了关于切换回归的集成模糊聚类算法 C均值聚类算法(fuzzy C clustering algorithm,FCM) (gravity-based fuzzy clustering algorithm,GFC)算法, 的基础上提出了模糊C均值回归算法(fuzzy C re- 文中实验表明该算法与CR相比具有更快的收敛 速度;文献[7]通过向FCR中引入动态的样本权值, 收稿日期:2015-08-14.网络出版日期:2016-08-24. 提出了离群模糊切换回归模型,从而使模型具有更 基金项目:国家自然科学基金项目(61300151):江苏省自然科学基金强的鲁棒性,并且能通过权值发现数据集中的离群 项目(BK20130155,BK20130160). 通信作者:刘欢.E-mail:771627297@qg.com. 点。虽然这些方法在一定条件下可以较好地解决切
第 11 卷第 5 期 智 能 系 统 学 报 Vol.11 №.5 2016 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2016 DOI:10.11992 / tis.201508015 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20160824.0928.002.html 堆叠隐空间模糊 C 回归算法及其在 发酵数据多模型建模中的应用 刘欢,王骏,邓赵红,王士同 (江南大学 数字媒体学院,江苏 无锡 214122) 摘 要:切换回归算法 FCR 的性能容易受到噪声点以及离群点的影响,同时该算法对于复杂数据的处理能力较差。 对此,文中提出一种基于堆叠隐空间的模糊 C 回归算法。 该算法将基于 ELM 特征映射技术,利用主成分分析进行特 征提取,再结合多层前馈神经网络学习结构对隐空间进行多次扩展和压缩。 实验结果表明,该算法具有更好的抗噪 性能,对模糊指数的变化不敏感,同时在处理复杂数据以及在多模型建模中更加精确、高效、稳定。 关键词:隐空间映射;极限学习机;主成分分析;模糊 C 回归算法;多层神经网络;多模型建模 中图分类号:TP181 文献标志码:A 文章编号:1673⁃4785(2016)05⁃0670⁃10 中文引用格式:刘欢,王骏,邓赵红,等.堆叠隐空间模糊 C 回归算法及其在发酵数据多模型建模中的应用[J]. 智能系统学报, 2016, 11(5): 670⁃679. 英文引用格式:LIU Huan, WANG Jun, DENG Zhaohong, et al. A cascaded hidden space fuzzy C⁃regression algorithm and its ap⁃ plication in multi⁃model modeling for the fermentation process [J]. CAAI transactions on intelligent systems, 2016,11(5): 670⁃679. A cascaded hidden space fuzzy C⁃regression algorithm and its application in multi⁃model modeling for the fermentation process LIU Huan, WANG Jun, DENG Zhaohong, WANG Shitong (School of Digital Media, JiangNan University, WuXi 214122, China) Abstract:The switching regression algorithm FCR is sensitive to noise data and outliers. The algorithm also has low levels of capability for dealing with complex data. In order to handle these problems, an improved fuzzy C⁃regres⁃ sion algorithm is proposed based on cascaded hidden space. In our method, principal component analysis is com⁃ bined with extreme machine learning feature mapping and multilayer feedforward neural networks. The experimental results show that our proposed method is more stable as regards noise data and outliers, and thus more suitable for handling complex data and multi⁃model modeling problems for the fermentation process. Keywords:hidden space feature mapping; extreme learning machine; principal component analysis; fuzzy C⁃re⁃ gression algorithm; multilayer neural network; multi⁃model modeling. 收稿日期:2015⁃08⁃14. 网络出版日期:2016⁃08⁃24. 基金项目:国家自然科学基金项目(61300151); 江苏省自然科学基金 项目(BK20130155,BK20130160). 通信作者:刘欢.E⁃mail:771627297@ qq.com. 切换回归模型在经济、数据挖掘等领域中有着 广泛的应用。 近年来,基于模糊聚类分析[1⁃4] 的切 换回归技术得到了广泛的研究。 如文献[5]在模糊 C 均值聚类算法(fuzzy C clustering algorithm, FCM) 的基础上提出了模糊 C 均值回归算法( fuzzy C re⁃ gression algorithm, FCR)算法,从而实现了对多个模 型的切换回归;在此基础上,文献[6]结合牛顿万有 引力定律提出了关于切换回归的集成模糊聚类算法 (gravity⁃based fuzzy clustering algorithm, GFC)算法, 文中实验表明该算法与 FCR 相比具有更快的收敛 速度;文献[7]通过向 FCR 中引入动态的样本权值, 提出了离群模糊切换回归模型,从而使模型具有更 强的鲁棒性,并且能通过权值发现数据集中的离群 点。 虽然这些方法在一定条件下可以较好地解决切

第5期 刘欢,等:堆叠隐空间模糊C回归算法及其在发酵数据多模型建模中的应用 .671. 换回归模型中的参数学习问题,但是面向现实生活 常用的激励函数有以下几种: 中的复杂数据,仍然有诸多局限性,其学习能力有待 1 Sigmoid: G(x)= (2 进一步提高。 1 exp(-x) 近年来,以极速学习机(extreme learning ma- Sine: G(x)=sin(x) (3 chine,ELM)为代表的单隐层前馈神经网络快速学 名-龙川2 (4) 习理论得到了研究人员的深入研究[81。研究表 Gaussian:G(x;,x)=exp(- 2c2 明,将ELM特征映射技术代替已有核方法中的核映 1.2模糊C回归算法及其问题分析 射,可以有效提高学习器的学习能力,目前该技术已 l993年Richard J.Hathaway)和James C. 被广泛用于分类、回归、聚类等学习任务中。结合已 Bezdek[i提出了FCR算法。该算法能在对观察数 有的研究工作,本文重点研究基于ELM隐空间学习 据进行模糊划分的同时估计出划分数据满足的回归 理论的切换回归模型。首先研究基于主成分分析 模型参数。设数据集D={(x1,少1),(x2,Y),, (principal component analysis,.PCA)[]的压缩隐空 (xnyn)},其中n是数据点个数,x=(x1,x2,, 间构建新方法。在此基础上,结合多层神经网络学 xa)∈R,为∈R表示观察数据模型,d是数据集的 习方法,将单隐层结构改造为多隐层结构)],提出 特征数。FCR算法构建的回归模型为 堆叠隐空间模糊C回归算法(cascaded hidden space y:=Bo0+B1+…+B FCR,CHS-FCR)。该方法通过使用层次化的学习 i=1,2,…,c;j=1,2,…,n (5) 结构对数据对象在不同层次上的表达形式进行抽 式中:c是模型数目,j是样本点个数,B为模型参 象,并通过重组低层概念来重新定义高层概念,从而 数。FCR算法的目标函数为 有效提高了学习系统处理复杂问题的能力。经实验 Jm=∑∑(y-)2 (6) 验证,该算法能有效地弥补经典FCR的若干不足, 在保证学习精度和学习效率的前提下,该方法对噪 式中“,是隶属度,且满足∑4,=1,山∈10,1, 声数据和离群点有很好的鲁棒性。 i=1,2,…,c)=1,2,…,n。m是模糊指数且 m>1。FCR使用式(7)来更新隶属度: 1相关工作 (y-a)-a-) k=1,2,…,C 1.1ELM隐空间 ∑,(6y-)-- 在ELM中,隐节点所形成的特征空间构成隐空 (7) 间)。其映射过程如下:I)随机生成权重矩阵W∈ FCR的目标函数是一个基于模糊划分的多模 Ra和偏移量矩阵B=[b,b2…b]T,其中L是ELM 型最小二乘拟合准则问题,任何现有的能解决加权 隐节点总数,d是原始数据的维数。2)将原始数据 最小二乘问题的方法都可以用来估计参数。模型参 映射到L维的隐空间中。每一个输入数据都是一个 数可以通过式(8)求解: d维的向量,x=[x,x2…x]T。该特征映射可以表 示为: B:= [X DXXDY (8) h(r)=[h(x)…h,(x)…h(x)]I= [G(01,b1,x)…G(0:,b:,x)…G(e,b,x)]T 式中:X∈2CR(是以(1,x)=(1,x,…,)为 (1) 行向量输入数据矩阵。Y∈2CR”是以输出y为行 式中G(x)是激励函数,其映射过程如图1所示。 向量的输出列向量:D:∈2CRx是以第j个对角 h(x=[h,(x)·h(x)…h,x] 元素的对角矩阵,D,=diag(a,a,…,%)。FCR算 ELM隐含层 法的步骤为: 1)给定模型参数c(1≤c≤n),模糊指数m>1, G(w.bx) G(wbx) 迭代终止条件ε>0,并初始化划分矩阵),迭代步 d)输入层 骤1=0; 2)根据式(8)计算模型参数B:; =x,…xJ 3)根据(y)2计算拟合误差,代入式(7)求 图1隐空间特征映射的过程 隶属度矩阵U; Fig.1 The process of hidden-space feature mapping 4)根据式(6)计算目标函数值,若
换回归模型中的参数学习问题,但是面向现实生活 中的复杂数据,仍然有诸多局限性,其学习能力有待 进一步提高。 近年来, 以极速学习机 ( extreme learning ma⁃ chine,ELM)为代表的单隐层前馈神经网络快速学 习理论得到了研究人员的深入研究[8⁃11] 。 研究表 明,将 ELM 特征映射技术代替已有核方法中的核映 射,可以有效提高学习器的学习能力,目前该技术已 被广泛用于分类、回归、聚类等学习任务中。 结合已 有的研究工作,本文重点研究基于 ELM 隐空间学习 理论的切换回归模型。 首先研究基于主成分分析 (principal component analysis, PCA) [12] 的压缩隐空 间构建新方法。 在此基础上,结合多层神经网络学 习方法,将单隐层结构改造为多隐层结构[13] ,提出 堆叠隐空间模糊 C 回归算法(cascaded hidden space FCR, CHS⁃FCR)。 该方法通过使用层次化的学习 结构对数据对象在不同层次上的表达形式进行抽 象,并通过重组低层概念来重新定义高层概念,从而 有效提高了学习系统处理复杂问题的能力。 经实验 验证,该算法能有效地弥补经典 FCR 的若干不足, 在保证学习精度和学习效率的前提下,该方法对噪 声数据和离群点有很好的鲁棒性。 1 相关工作 1.1 ELM 隐空间 在 ELM 中,隐节点所形成的特征空间构成隐空 间[14] 。 其映射过程如下:1)随机生成权重矩阵W∈ R L×d和偏移量矩阵 B= [b1 b2… bL ] T ,其中 L 是 ELM 隐节点总数,d 是原始数据的维数。 2)将原始数据 映射到 L 维的隐空间中。 每一个输入数据都是一个 d 维的向量,x = [x1 x2… xd ] T 。 该特征映射可以表 示为: h(x) = [h1(x) … hi(x) … hL(x)] T = [G w1 ,b ( 1 ,x) … G wi,b ( i,x) … G wL ,b ( L ,x) ] T (1) 式中 G(x)是激励函数,其映射过程如图 1 所示。 图 1 隐空间特征映射的过程 Fig.1 The process of hidden⁃space feature mapping 常用的激励函数有以下几种: Sigmoid: G(x) = 1 1 + exp( - x) (2) Sine: G(x) = sin(x) (3) Gaussian:G(xi,xj) = exp( - ‖xi - xj‖2 2σ 2 ) (4) 1.2 模糊 C 回归算法及其问题分析 1993 年 Richard J. Hathaway [5] 和 James C. Bezdek [15]提出了 FCR 算法。 该算法能在对观察数 据进行模糊划分的同时估计出划分数据满足的回归 模型参数。 设数据集 D = {( x1 , y1 ), ( x2 , y2 ),…, (xn ,yn )},其中 n 是数据点个数,xj = ( xj1 ,xj2 ,…, xjd )∈R d ,yj∈R 表示观察数据模型,d 是数据集的 特征数。 FCR 算法构建的回归模型为 yj,i = βi0 + βi1 xj1 + … + βid xjd i = 1,2,…,c; j = 1,2,…,n (5) 式中:c 是模型数目,j 是样本点个数,βi 为模型参 数。 FCR 算法的目标函数为 JFCR = ∑ c i = 1∑ n j = 1 u m ij (yj - yj,i) 2 (6) 式中 uij是隶属度,且满足 ∑ c i = 1 uij = 1,uij ∈ {0,1}, i = 1,2,…,c;j = 1,2,…,n。 m 是 模 糊 指 数 且 m > 1。 FCR 使用式(7)来更新隶属度: uij = (yj - yj,i) -2/ (m-1) ∑ c k = 1 (yj - yj,k) -2/ (m-1) k = 1,2,…,c (7) FCR 的目标函数是一个基于模糊划分的多模 型最小二乘拟合准则问题,任何现有的能解决加权 最小二乘问题的方法都可以用来估计参数。 模型参 数可以通过式(8)求解: βi = βi0 ︙ βid é ë ê ê ê ê ù û ú ú ú ú = [X T DiX] -1 X T DiY (8) 式中:X∈Ω⊂R n×(d+1)是以(1,xj)= (1,xj1 ,…,xjd )为 行向量输入数据矩阵。 Y∈Ω⊂R n 是以输出 yj 为行 向量的输出列向量;Di∈Ω⊂R n×n是以 u m ij 第 j 个对角 元素的对角矩阵,Di = diag(u m i1 ,u m i1 ,…,u m in )。 FCR 算 法的步骤为: 1)给定模型参数 c(1≤c≤n),模糊指数 m>1, 迭代终止条件 ε>0,并初始化划分矩阵 U (0) ,迭代步 骤 l = 0; 2)根据式(8)计算模型参数 β l i; 3)根据(yj -yj,i) 2 计算拟合误差,代入式(7)求 隶属度矩阵 U; 4 ) 根 据 式 ( 6 ) 计 算 目 标 函 数 值, 若 第 5 期 刘欢,等:堆叠隐空间模糊 C 回归算法及其在发酵数据多模型建模中的应用 ·671·

·672 智能系统学报 第11卷 IJ化-Jc0川≤e则迭代终止,其中e表示迭代 PCA隐含层 终止的阈值:否则1=+1,转至步骤2)。 PCA 研究表明,FCR可以较好地解决切换回归问 题,但是也存在以下问题:对噪声和离群点敏感,当 数据集中含有离群点或大量噪声数据时,算法性能 h h,xELM隐含层 就会受到影响:FCR算法在数据原空间中进行学 Gwbx) w.b.x) 习,针对现实生活中的复杂数据,FCR算法的性能 很难得到有效地提升。 输入层 本文将ELM隐空间学习理论与特征降维技术 相结合,基于多隐层神经网络学习方法,将传统的基 于浅层结构的学习方法改造为多隐层学习结构,从 图2基于PCA的压缩ELM隐空间 而提高对复杂数据的无监督学习能力。通过提出堆 Fig.2 Cascade hidden space based on PCA 叠隐空间学习结构,从而有效精简冗余信息和过滤 2.2 噪声数据,同时补充必要的信息,使得切换回归算法 堆叠隐空间模糊C回归算法CHS-FCR 具有更强的鲁棒性,并将其应用于多模型建模以取 在隐空间构建过程中,为了使学习器得到更好 得更好的效果。 的表达能力和稳定的学习效果,通常会使用较多的 隐节点数目。但是,这增加了额外的计算负担。研 2堆叠隐空间模糊C回归算法 究表明,在保证学习器泛化能力的前提下,将单隐层 2.1基于主成分分析的压缩ELM隐空间 结构改造为多隐层结构是降低隐节点数目的有效方 在ELM学习技术中,可以通过随机赋值的方法 法。为此,本文对上述基于PCA的压缩隐空间映射 来快速生成ELM隐空间,随着隐节点数目的增加, 过程进行改造,通过把ELM隐层中的隐节点分散到 学习精度也不断提高161)。但是随之而来的一个 多个隐含层中,并与PCA层的隐结点相结合,形成 重要问题是计算效率会逐步降低。此外,由于隐节 新的混合隐含层。将若干个混合隐含层进行叠加, 点生成过程中相关参数是随机生成的,因此不可避 得到多隐层学习结构,该过程如图3所示。 免地会引入大量噪声。针对这一问题,本文中将 PCA隐含层Q月 ELM隐空间技术与主成分分析相结合,提出基于主 PCA 成分分析的压缩隐空间构建方法,其过程如下: 1)根据图1所示过程将原始数据映射到高维 混合隐含层 空间R中,得到矩阵H)∈RM,n为样本点个数: ELM特征射 PCA :输入层 2)对H的每一列H,j=1,2,…,L进行归 混合隐含层 一化,得到矩阵A=[A1A2…A],其中A计算方 /ELM特征映射 法为 PCA 输人层 4="-12H"=12,…,1 ELM隐含层 (9) n i=1 ELM特征映射 输入层 3)计算矩阵A的协方差矩阵C,并计算矩阵C 的特征值入和特征向量V,i=1,2,…,L: 4)将特征值入:降序排序,取前p个特征值对应 的特征向量,按列组成矩阵V,特征提取后的矩阵为 图3堆叠隐空间学习结构 Fig.3 Cascade hidden space learning structure H)=AV (10) 其结构可映射为如图2所示的前馈神经网络模 堆叠隐空间模糊C回归算法CHS-FCR的描述 型。输入数据经过输入层后,通过ELM特征映射被 如下: 映射到高维ELM隐空间中。在此过程中,生成ELM 设隐节点总数为L,数据集D的维数为d,PCA 隐空间时的随机赋值操作会引入噪声,后续的PCA 压缩后的维数为P,隐空间压缩的次数为f,每层隐 对高维隐空间中的数据进行降维,从而有效地过滤 空间的ELM隐节点数T=L/f,n为样本点个数。 掉部分噪声,这有利于提高学习性能。 1)①随机生成值在[0,1]之间的权重矩阵
‖J (l+1) FCR -JFCR (l)‖≤ε则迭代终止,其中 ε 表示迭代 终止的阈值;否则 l = l+1,转至步骤 2)。 研究表明,FCR 可以较好地解决切换回归问 题,但是也存在以下问题:对噪声和离群点敏感,当 数据集中含有离群点或大量噪声数据时,算法性能 就会受到影响;FCR 算法在数据原空间中进行学 习,针对现实生活中的复杂数据,FCR 算法的性能 很难得到有效地提升。 本文将 ELM 隐空间学习理论与特征降维技术 相结合,基于多隐层神经网络学习方法,将传统的基 于浅层结构的学习方法改造为多隐层学习结构,从 而提高对复杂数据的无监督学习能力。 通过提出堆 叠隐空间学习结构,从而有效精简冗余信息和过滤 噪声数据,同时补充必要的信息,使得切换回归算法 具有更强的鲁棒性,并将其应用于多模型建模以取 得更好的效果。 2 堆叠隐空间模糊 C 回归算法 2.1 基于主成分分析的压缩 ELM 隐空间 在 ELM 学习技术中,可以通过随机赋值的方法 来快速生成 ELM 隐空间,随着隐节点数目的增加, 学习精度也不断提高[16⁃17] 。 但是随之而来的一个 重要问题是计算效率会逐步降低。 此外,由于隐节 点生成过程中相关参数是随机生成的,因此不可避 免地会引入大量噪声。 针对这一问题,本文中将 ELM 隐空间技术与主成分分析相结合,提出基于主 成分分析的压缩隐空间构建方法,其过程如下: 1)根据图 1 所示过程将原始数据映射到高维 空间 R L 中,得到矩阵 H (1)∈R n×L ,n 为样本点个数; 2)对 H (1) 的每一列 H (1) j ,j = 1,2,…,L 进行归 一化,得到矩阵 A = [A1 A2… AL ],其中 Aj 计算方 法为 Aj = H (1) j - 1 n ∑ N j = 1 H (1) j ,j = 1,2,…,L (9) 3)计算矩阵 A 的协方差矩阵 C,并计算矩阵 C 的特征值 λi 和特征向量 Vi,i = 1,2,…,L; 4)将特征值 λi 降序排序,取前 p 个特征值对应 的特征向量,按列组成矩阵 V ~ ,特征提取后的矩阵为 H (2) = AV ~ (10) 其结构可映射为如图 2 所示的前馈神经网络模 型。 输入数据经过输入层后,通过 ELM 特征映射被 映射到高维 ELM 隐空间中。 在此过程中,生成 ELM 隐空间时的随机赋值操作会引入噪声,后续的 PCA 对高维隐空间中的数据进行降维,从而有效地过滤 掉部分噪声,这有利于提高学习性能。 图 2 基于 PCA 的压缩 ELM 隐空间 Fig.2 Cascade hidden space based on PCA 2.2 堆叠隐空间模糊 C 回归算法 CHS⁃FCR 在隐空间构建过程中,为了使学习器得到更好 的表达能力和稳定的学习效果,通常会使用较多的 隐节点数目。 但是,这增加了额外的计算负担。 研 究表明,在保证学习器泛化能力的前提下,将单隐层 结构改造为多隐层结构是降低隐节点数目的有效方 法。 为此,本文对上述基于 PCA 的压缩隐空间映射 过程进行改造,通过把 ELM 隐层中的隐节点分散到 多个隐含层中,并与 PCA 层的隐结点相结合,形成 新的混合隐含层。 将若干个混合隐含层进行叠加, 得到多隐层学习结构,该过程如图 3 所示。 图 3 堆叠隐空间学习结构 Fig.3 Cascade hidden space learning structure 堆叠隐空间模糊 C 回归算法 CHS⁃FCR 的描述 如下: 设隐节点总数为 L,数据集 D 的维数为 d,PCA 压缩后的维数为 p,隐空间压缩的次数为 f,每层隐 空间的 ELM 隐节点数 T = L / f,n 为样本点个数。 1)① 随机生成值在[ 0,1] 之间的权重矩阵 ·672· 智 能 系 统 学 报 第 11 卷

第5期 刘欢,等:堆叠隐空间模糊C回归算法及其在发酵数据多模型建模中的应用 .673 WeR以及值在[0.5,1]之间的偏移量矩阵B∈R。 表1实验平台 ②根据式(1)以及图1将数据集D进行特征映 Table 1 Experimental platform 射,得到高维数据矩阵H)∈Rxr。 结构 配置 2)利用基于PCA的压缩隐空间方法对H)进 CPU Intel(R)Core(TM)i5-4590 3.30GHz 行压缩,得到维数为p的数据矩阵H2): 内存 8.00GB 操作系统 64bit Windows7 3)for j=1:f-1 软件平台 Matlab R2012a ①重复步骤1中1)、2); 3.2鲁棒性实验 ②将H2)与H)合并存入矩阵H3)中, 本实验中,基于文献[5]的模拟回归数据集,通 H3)=[H2H)]。 过分别加入噪声点和离群点来比较FCR以及CHS, ③利用PCA对H3)进行特征提取,得到矩阵记 FCR算法的鲁棒性。实验中,FCR算法和CHS-FCR 为H2; 算法的模型个数c=2,模糊指数m=2,CHS-FCR隐 循环结束; 空间压缩次数f=5,PCA特征提取后的维数p=3。 4)构造全一矩阵1∈Rax1,将最终获取的数据 3.2.1离群点实验 H2=[1,2)]利用FCR框架进行切换回归。 在切换回归分析中,离群点主要是指不符合任 CHS-FCR算法将基于PCA的压缩ELM隐空间 一模型的数据,它主要是在收集数据的过程中出现 单隐层学习结构改造为多隐层学习结构。假设从第 误操作或异常情况而引入的。本实验中基于式 二层开始,每个隐含层中随机生成的ELM隐节点数 (15)和(16)生成2个回归数据集,并分别加入离群 都是T,由前一层PCA压缩后得到的隐节点数为 点(16,8)。实验数据集分布如图4所示。 T',易得隐节点总数为 L=(T+T)×(f-1)+T (11) y1=18-x+0.03125x2 A: (15) 其中随机生成的ELM隐节点总数为 0y2=-2+x-0.03125x2 LELM =Txf (12) y1=172-26x+x2 经过多次隐空间压缩,噪声信息被过滤,同时会 B: (16) y2=364-38x+x2 发生相应的信息损失:但是每个混合层中新生成的 图5和图6给出了加入离群点之前模糊C均值 ELM隐节点信息弥补了这些丢失的信息,因此本文 回归算法(fuzzy C regression algorithm,FCR)和堆叠 的堆叠隐空间结构能得到更好的学习效果。 隐空间模糊C回归算法(cascaded hidden space 3实验研究与分析 FCR,CHS-FCR)的回归结果,图7和图8给出了加 入离群点之后两算法的回归结果。从中可以看出, 3.1实验平台以及算法性能的评价指标 加入离群点之前,FCR和CHS-FCR这2个算法均可 本文在表1中实验平台上进行所有实验并且采 以得到理想的结果。加入离群点之后,CR的拟合 用式(13)和(14)所示的指标来评价各算法的性能。 效果明显受到离群点的影响:但是CHS-FCR仍然能 得到令人满意的拟合结果。可见,压缩隐空间方法 的引入使本文所提的CHS-FCR算法对离群点具有 (13) 更好的鲁棒性。 12 11 [(1r,-()] 9 (14) 式中:N表示测试样本数,y:表示测试样本第i次输 6 入的输出,y:'表示测试样本第i次输入的模糊系统 输出,y=∑y:。式(13)和(14)所示的指标数值 1012141618202224 分别越接近于0和1,则算法的性能越好。 (a)数据集A
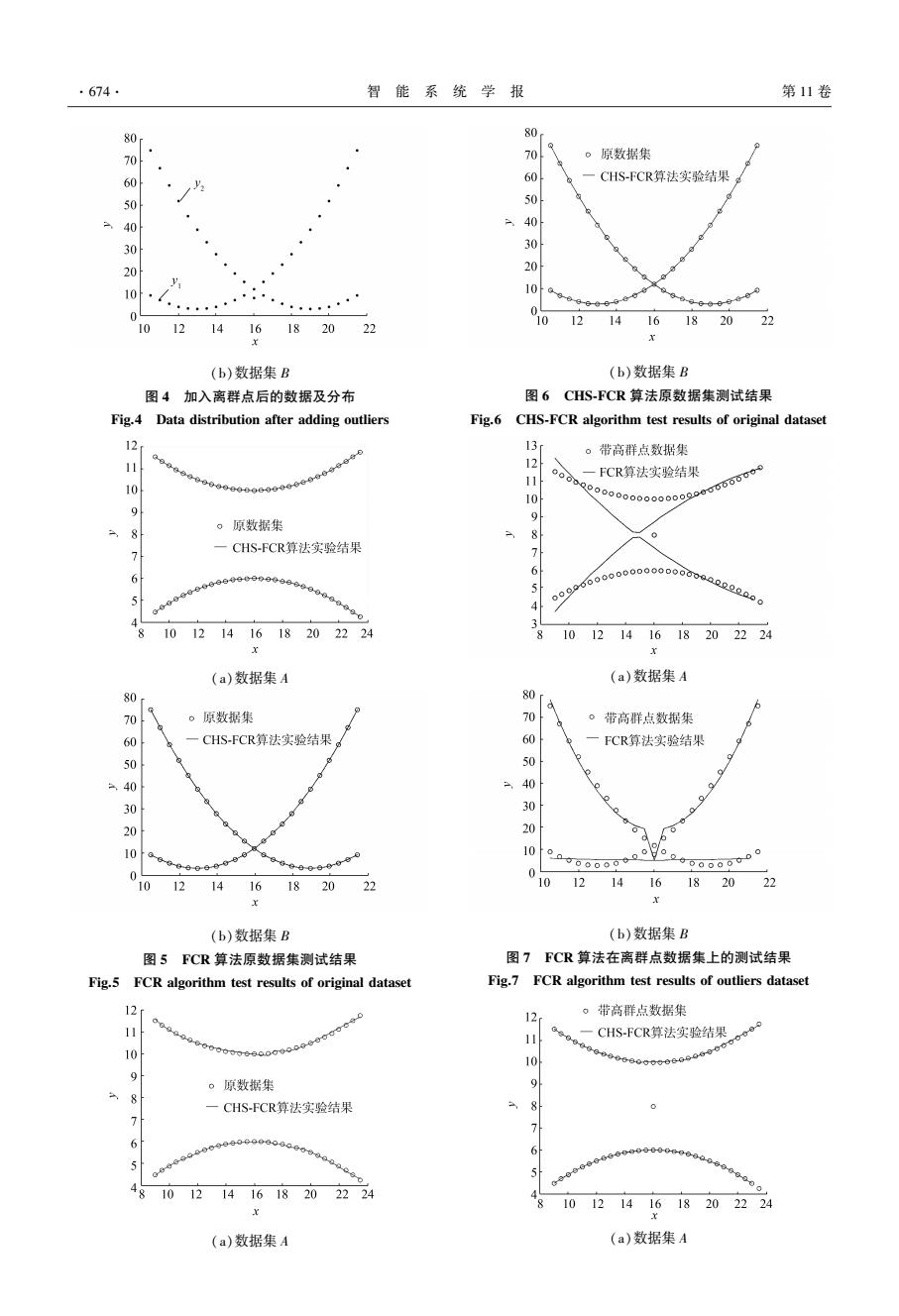
W∈R T×d以及值在[0.5,1]之间的偏移量矩阵 B∈R T×1 。 ②根据式(1)以及图 1 将数据集 D 进行特征映 射,得到高维数据矩阵 H (1)∈R n×T 。 2)利用基于 PCA 的压缩隐空间方法对 H (1) 进 行压缩,得到维数为 p 的数据矩阵H (2) ; 3)for j = 1:f-1 ①重复步骤 1 中 1)、2); ② 将 H (2) 与 H (1) 合 并 存 入 矩 阵 H (3) 中, H (3)= [H (2) H (1) ]。 ③利用 PCA 对 H (3)进行特征提取,得到矩阵记 为 H (2) ; 循环结束; 4)构造全一矩阵 1∈R n×1 ,将最终获取的数据 H (2)= [1,H (2) ]利用 FCR 框架进行切换回归。 CHS⁃FCR 算法将基于 PCA 的压缩 ELM 隐空间 单隐层学习结构改造为多隐层学习结构。 假设从第 二层开始,每个隐含层中随机生成的 ELM 隐节点数 都是 T,由前一层 PCA 压缩后得到的隐节点数为 T′,易得隐节点总数为 L = (T + T′) × (f - 1) + T (11) 其中随机生成的 ELM 隐节点总数为 LELM = T × f (12) 经过多次隐空间压缩,噪声信息被过滤,同时会 发生相应的信息损失;但是每个混合层中新生成的 ELM 隐节点信息弥补了这些丢失的信息,因此本文 的堆叠隐空间结构能得到更好的学习效果。 3 实验研究与分析 3.1 实验平台以及算法性能的评价指标 本文在表 1 中实验平台上进行所有实验并且采 用式(13)和(14)所示的指标来评价各算法的性能。 JRRSE = 1 N∑ N i = 1 (yi ′ - yi) 2 / 1 N∑ N i = 1 (yi - y - ) 2 (13) JSCC = N∑ N i = 1 yi ′·y ( i) 2 N∑ N i = 1 (yi ′) 2- (∑ N i = 1 yi) 2 [ ]· N∑ N i = 1 (yi) 2-(∑ N i = 1 yi) 2 [ ] (14) 式中:N 表示测试样本数,yi 表示测试样本第 i 次输 入的输出,yi ′表示测试样本第 i 次输入的模糊系统 输出, y - = 1 N∑ N i = 1 yi 。 式(13)和(14)所示的指标数值 分别越接近于 0 和 1,则算法的性能越好。 表 1 实验平台 Table 1 Experimental platform 结构 配置 CPU Intel(R)Core(TM) i5-4590 3.30GHz 内存 8.00 GB 操作系统 64bit Windows7 软件平台 Matlab R2012a 3.2 鲁棒性实验 本实验中,基于文献[5]的模拟回归数据集,通 过分别加入噪声点和离群点来比较 FCR 以及 CHS⁃ FCR 算法的鲁棒性。 实验中,FCR 算法和 CHS⁃FCR 算法的模型个数 c = 2,模糊指数 m = 2,CHS⁃FCR 隐 空间压缩次数 f = 5,PCA 特征提取后的维数 p = 3。 3.2.1 离群点实验 在切换回归分析中,离群点主要是指不符合任 一模型的数据,它主要是在收集数据的过程中出现 误操作或异常情况而引入的。 本实验中基于式 (15)和(16)生成 2 个回归数据集,并分别加入离群 点(16,8)。 实验数据集分布如图 4 所示。 A: y1 = 18 - x + 0.031 25x 2 y2 = - 2 + x - 0.031 25x { 2 (15) B: y1 = 172 - 26x + x 2 y2 = 364 - 38x + x { 2 (16) 图 5 和图 6 给出了加入离群点之前模糊 C 均值 回归算法(fuzzy C regression algorithm, FCR)和堆叠 隐空 间 模 糊 C 回 归 算 法 ( cascaded hidden space FCR, CHS⁃FCR)的回归结果,图 7 和图 8 给出了加 入离群点之后两算法的回归结果。 从中可以看出, 加入离群点之前,FCR 和 CHS⁃FCR 这 2 个算法均可 以得到理想的结果。 加入离群点之后,FCR 的拟合 效果明显受到离群点的影响;但是 CHS⁃FCR 仍然能 得到令人满意的拟合结果。 可见,压缩隐空间方法 的引入使本文所提的 CHS⁃FCR 算法对离群点具有 更好的鲁棒性。 (a)数据集 A 第 5 期 刘欢,等:堆叠隐空间模糊 C 回归算法及其在发酵数据多模型建模中的应用 ·673·
674 智能系统学报 第11卷 80 。原数据集 60 0 CHS-FCR算法实验结果 % 吃 40 30 20 20 10 10 8.e 0 0 12 14 16 18 20 22 1416182022 (b)数据集B (b)数据集B 图4加入离群点后的数据及分布 图6CHS-FCR算法原数据集测试结果 Fig.4 Data distribution after adding outliers Fig.6 CHS-FCR algorithm test results of original dataset 12 13 6 。带高群点数据集 11 12 一FCR算法实验结果 11 10 10 9 。原数据集 8 CHS-FCR算法实验结果 7 7 6 5 5 10 12 141618202224 8 10 1214 1618202224 (a)数据集A (a)数据集A 光 80r d 。原数据集 70 ·带高群点数据集 一CHS-FCR算法实验结果 60 FCR算法实验结果 吃 50 ,40 .40 30 30 a 20 20 6 10 100a。。0o61900.00o00 0 0 12 1416 1820 22 10 12 14 16 18 20 22 (b)数据集B (b)数据集B 图5FCR算法原数据集测试结果 图7FCR算法在离群点数据集上的测试结果 Fig.5 FCR algorithm test results of original dataset Fig.7 FCR algorithm test results of outliers dataset 12 12 。带高群点数据集 11 CHS-FCR算法实验结果 10 10 9 。原数据集 9 一CHS-FCR算法实险结果 7 7 6 6 5 r 5 1012141618202224 1012141618202224 (a)数据集A (a)数据集A
(b)数据集 B 图 4 加入离群点后的数据及分布 Fig.4 Data distribution after adding outliers (a)数据集 A (b)数据集 B 图 5 FCR 算法原数据集测试结果 Fig.5 FCR algorithm test results of original dataset (a)数据集 A (b)数据集 B 图 6 CHS⁃FCR 算法原数据集测试结果 Fig.6 CHS⁃FCR algorithm test results of original dataset (a)数据集 A (b)数据集 B 图 7 FCR 算法在离群点数据集上的测试结果 Fig.7 FCR algorithm test results of outliers dataset (a)数据集 A ·674· 智 能 系 统 学 报 第 11 卷