
第10卷第6期 智能系统学报 Vol.10 No.6 2015年12月 CAAI Transactions on Intelligent Systems Dee.2015 D0:10.11992.tis.201505043 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.tp.20151110.1354.006.html 融合并行混沌萤火虫算法的K-调和均值聚类 朱书伟,周治平,张道文 (江南大学物联网工程学院,江苏无锡214122) 摘要:针对K-调和均值算法易陷于局部最优的缺点,提出一种基于改进萤火虫算法(firefly algorithm,FA)的K-调 和均值聚类算法。将基于FA的粗搜索与基于并行混沌优化FA的精细搜索相结合,其中精细搜索部分首先通过FA 搜索到当前最优解及次优解,然后通过改进的1 ogistic映射与并行混沌优化策略产生混沌序列在其附近直接搜索,以 增强算法的寻优性能。最终,将这种改进的FA用于K调和均值算法聚类中心的优化。实验结果表明:该算法不但 对几种测试函数具有更高的搜索精度,而且对6种数据集的聚类结果均有一定的改善,有效地抑制了K-调和均值算 法陷于局部最优的问题,提高了聚类准确性和稳定性。 关键词:K调和均值:局部最优:莹火虫算法;聚类:并行混沌优化:混沌局部搜索:映射模型:种群多样性 中图分类号:TP18文献标志码:A文章编号:1673-4785(2015)06-0872-09 中文引用格式:朱书伟,周治平,张道文.融合并行混沌萤火虫算法的K-调和均值聚类[J].智能系统学报,2015,10(6):872-880. 英文引用格式:ZHU Shuwei,ZHOU Zhiping,ZHANG Daowen.K-harmonic means clustering merged with parallel chaotic firefly algorithm[J].CAAI Transactions on Intelligent Systems,2015,10(6):872-880. K-harmonic means clustering merged with parallel chaotic firefly algorithm ZHU Shuwei,ZHOU Zhiping,ZHANG Daowen (School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,China) Abstract:The K-harmonic means algorithm (KHM)has the disadvantage of easily falling into a local optimum.To solve this problem,we propose a hybrid KHM based on an improved firefly algorithm(FA).In this paper,we com- bined raw FA-based searching with parallel chaotic FA-based elaborate searching.In the elaborate searching,we found the current best and second-best solutions using the FA,then we used an improved logistic map model com- bined with parallel chaotic optimization to search this area in order to enhance the searching ability of the algorithm. Finally,we used the improved FA to optimize the cluster centers obtained by the KHM.Experimental results dem- onstrate that the proposed algorithm not only had higher search precision for several test functions,but also im- proved the clustering accuracy and stability of six datasets,effectively avoiding being trapped into a local optimum. Keywords:K-harmonic means;local optimum;firefly algorithm;clustering;parallel chaotic optimization;chaotic local search;map model;diversity of population 聚类分析是一种广泛使用的数据分析方法,一 最经典且使用最为广泛的聚类算法,其过程简单快 直被应用于多个领域,特别是在数据挖掘、模式识 捷,容易实现。为了克服K-means对初始聚类中心 别、图像处理等领域应用十分广泛。K-meanst是 敏感的缺陷,Zhang等)于1999年提出一种K-调和 均值(K-harmonic means,KHM)算法,具有较高的稳 收稿日期:2015-05-27.网络出版日期:2015-11-10. 定性、收敛速度快,但由于其与K-means同样基于划 基金项目:江苏省产学研联合创新资金-前瞻性联合研究基金资助项目 (BY2013015-33). 分的原理,仍存在易陷于局部最优的问题。 通信作者:朱书伟.E-mail:6131905056@ip-jiangnan.cdu.cm 目前,对于KHM算法的研究主要是结合智能
第 10 卷第 6 期 智 能 系 统 学 报 Vol.10 №.6 2015 年 12 月 CAAI Transactions on Intelligent Systems Dec. 2015 DOI:10.11992.tis.201505043 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20151110.1354.006.html 融合并行混沌萤火虫算法的 K⁃调和均值聚类 朱书伟,周治平,张道文 (江南大学 物联网工程学院,江苏 无锡 214122) 摘 要:针对 K⁃调和均值算法易陷于局部最优的缺点,提出一种基于改进萤火虫算法(firefly algorithm, FA)的 K⁃调 和均值聚类算法。 将基于 FA 的粗搜索与基于并行混沌优化 FA 的精细搜索相结合,其中精细搜索部分首先通过 FA 搜索到当前最优解及次优解,然后通过改进的 logistic 映射与并行混沌优化策略产生混沌序列在其附近直接搜索,以 增强算法的寻优性能。 最终,将这种改进的 FA 用于 K⁃调和均值算法聚类中心的优化。 实验结果表明:该算法不但 对几种测试函数具有更高的搜索精度,而且对 6 种数据集的聚类结果均有一定的改善,有效地抑制了 K⁃调和均值算 法陷于局部最优的问题,提高了聚类准确性和稳定性。 关键词:K⁃调和均值;局部最优;萤火虫算法;聚类;并行混沌优化;混沌局部搜索;映射模型;种群多样性 中图分类号:TP18 文献标志码:A 文章编号:1673⁃4785(2015)06⁃0872⁃09 中文引用格式:朱书伟,周治平, 张道文. 融合并行混沌萤火虫算法的 K⁃调和均值聚类[J]. 智能系统学报, 2015, 10(6): 872⁃880. 英文引用格式:ZHU Shuwei, ZHOU Zhiping, ZHANG Daowen. K⁃harmonic means clustering merged with parallel chaotic firefly algorithm[J]. CAAI Transactions on Intelligent Systems, 2015, 10(6): 872⁃880. K⁃harmonic means clustering merged with parallel chaotic firefly algorithm ZHU Shuwei, ZHOU Zhiping, ZHANG Daowen (School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China) Abstract:The K⁃harmonic means algorithm (KHM) has the disadvantage of easily falling into a local optimum. To solve this problem, we propose a hybrid KHM based on an improved firefly algorithm (FA). In this paper, we com⁃ bined raw FA⁃based searching with parallel chaotic FA⁃based elaborate searching. In the elaborate searching, we found the current best and second⁃best solutions using the FA, then we used an improved logistic map model com⁃ bined with parallel chaotic optimization to search this area in order to enhance the searching ability of the algorithm. Finally, we used the improved FA to optimize the cluster centers obtained by the KHM. Experimental results dem⁃ onstrate that the proposed algorithm not only had higher search precision for several test functions, but also im⁃ proved the clustering accuracy and stability of six datasets, effectively avoiding being trapped into a local optimum. Keywords: K⁃harmonic means; local optimum; firefly algorithm; clustering; parallel chaotic optimization; chaotic local search; map model; diversity of population 收稿日期:2015⁃05⁃27. 网络出版日期:2015⁃11⁃10. 基金项目:江苏省产学研联合创新资金-前瞻性联合研究基金资助项目 (BY2013015⁃33). 通信作者:朱书伟. E⁃mail:6131905056@ vip.jiangnan.edu.cn. 聚类分析是一种广泛使用的数据分析方法,一 直被应用于多个领域,特别是在数据挖掘、模式识 别、图像处理等领域应用十分广泛。 K⁃means [1] 是 最经典且使用最为广泛的聚类算法,其过程简单快 捷,容易实现。 为了克服 K⁃means 对初始聚类中心 敏感的缺陷,Zhang 等[2]于 1999 年提出一种 K⁃调和 均值(K⁃harmonic means, KHM)算法,具有较高的稳 定性、收敛速度快,但由于其与 K⁃means 同样基于划 分的原理,仍存在易陷于局部最优的问题。 目前,对于 KHM 算法的研究主要是结合智能

第6期 朱书伟,等:融合并行混沌莹火虫算法的K-调和均值聚类 ·873. 优化算法进行改进,以充分利用其全局搜索能力,如 这里采用欧式距离计算样本到聚类中心的 融合粒子群)、变邻域搜索)、改进候选组搜索) 距离,参数p对算法的性能具有重要的影响,且 等混合聚类算法。此外,将模糊概念引入KHM中 当p≥2时聚类的效果比较好2]。算法通过不断 也得到了一定的关注6)。目前,各种群智能优化 地迭代使目标函数值不断减小并保持稳定,每次 算法已被广泛地应用于各个领域中[81),并且依据 迭代过程中,各个簇的中心点c()=1,2,…,k)的 没有免费的午餐定律,本文提出新的混合聚类算法。 更新如下[3) 萤火虫算法(firefly algorithm,FA)是由剑桥学者 Yang等[2.1)在2008年提出的一种新颖的群智能算 ∑,mw(c/x)XU(x)Xx i=1 (2) 法,具有结构简单、可调参数少、宜于并行处理等特 点,可以有效解决各种优化问题,并能够成功应用到 ∑mum(cy/x,)X0uw() 聚类问题中提高算法的准确性和鲁棒性[。很多 式中:成员函数m和权重函数wKv的定义分别为 学者已经对它开展了不少研究工作,引入混沌原理 式(3)和式(4)。 改进的FA具有一定的优势,Fister等[s]对现有的混 Ix:-c‖p-2 mkH(C/x:)= (3) 沌萤火虫算法(chaos-based firefly algorithm,CFA) lx-l-p-2 进行了总结,它们的主要思想都是基于算法参数的 改进,其中Gandomi等[u6]采用各种混沌映射模型进 x-6 WKHM(x:)= (4) 行了比较全面的对比分析。然而,仅对参数的调整 (,g-6) 无法更全面有效地利用混沌优化的优点,混沌局部 1.2 萤火虫算法的相关定义 搜索(chaotic local search,CLS)[91o]是一种能够有 在FA中萤火虫彼此吸引主要取决于2个因 效提高算法优化性能的策略。 素:亮度和吸引度。亮度决定了个体所处位置的好 本文从进一步提高FA的优化性能出发,提出 坏及其移动方向,吸引度决定了移动的距离,通过亮 一种新颖的CFA,并将其融入到KHM以获得一种 度和吸引度的不断更新,实现目标优化。通常直接 更有效的混合聚类方法。在FA中引入一种并行混 利用目标函数值的大小表示萤火虫i的亮度I,即 沌局部搜索策略,将CLS与并行混沌优化(parallel L=f:),x:=[xax2…xa]。FA的相关定 chaotic optimization,PC0)[7-l8]相结合,提高FA的 义如下12.13 局部搜索能力,具有更高的搜索效率,并能够有效避 定义1萤火虫i与j之间的吸引度为 免局部最优。将这种改进的CFA融入到KHM中优 B=Boe-r (5) 化其目标函数,通过对实际数据集的实验可以看出 式中:B。为在r=0处的吸引度,一般可取值为1;y 本文所提的聚类算法能够获得更好的性能指标,有 为光强吸收系数,对算法的性能具有重要的影响,通 效抑制了陷入局部最优的问题。 常情况下可以取y=1;r,为萤火虫i与j之间的空 1算法概念与定义 间距离,一般采用欧氏距离计算。 定义2萤火虫i被更亮的萤火虫j吸引而移 1.1K-调和均值算法 动的位置为 K-调和均值算法的原理基本上与K-means是相 xi=x;+B(Xi-xi)+aEi (6) 似的,不同的是其使用调和均值(harmonic means, 式中:x:、x为萤火虫i和j的位置:a为步长因子, HM)代替算术均值来计算目标函数,能够有效解决 可设为常数:e:为服从均匀分布的随机数向量。 对初始类中心点选取的敏感性问题。假定数据集 X=[x1x2…x.]包含n个数据,它们被划分 2基于改进FA的K-调和均值聚类 到k个聚类簇,每个簇的中心用c,(G=1,2,…,k)表 2.1并行混沌局部搜索策略改进的FA 示,KHM的目标函数为[) 基本的FA缺乏变异机制,当处于局部极值时 KHM(X,C)= -,i=1,2,…,n 难以摆脱,且当前最优解xg周围是搜索到更优解的 1 最有利的区域,而FA在优化过程中采用对其随机 2x:-G1 扰动的方式,搜索效率不高。混沌优化方法能够有 (1) 效地跳出局部最优并搜索到全局最优解,现有文献
优化算法进行改进,以充分利用其全局搜索能力,如 融合粒子群[3] 、变邻域搜索[4] 、改进候选组搜索[5] 等混合聚类算法。 此外,将模糊概念引入 KHM 中 也得到了一定的关注[6⁃7] 。 目前,各种群智能优化 算法已被广泛地应用于各个领域中[8⁃11] ,并且依据 没有免费的午餐定律,本文提出新的混合聚类算法。 萤火虫算法( firefly algorithm, FA) 是由剑桥学者 Yang 等[12⁃13]在 2008 年提出的一种新颖的群智能算 法,具有结构简单、可调参数少、宜于并行处理等特 点,可以有效解决各种优化问题,并能够成功应用到 聚类问题中提高算法的准确性和鲁棒性[14] 。 很多 学者已经对它开展了不少研究工作,引入混沌原理 改进的 FA 具有一定的优势,Fister 等[15]对现有的混 沌萤火虫算法( chaos⁃based firefly algorithm, CFA) 进行了总结,它们的主要思想都是基于算法参数的 改进,其中 Gandomi 等[16]采用各种混沌映射模型进 行了比较全面的对比分析。 然而,仅对参数的调整 无法更全面有效地利用混沌优化的优点,混沌局部 搜索( chaotic local search, CLS) [9⁃10] 是一种能够有 效提高算法优化性能的策略。 本文从进一步提高 FA 的优化性能出发,提出 一种新颖的 CFA,并将其融入到 KHM 以获得一种 更有效的混合聚类方法。 在 FA 中引入一种并行混 沌局部搜索策略,将 CLS 与并行混沌优化( parallel chaotic optimization, PCO) [17⁃18] 相结合,提高 FA 的 局部搜索能力,具有更高的搜索效率,并能够有效避 免局部最优。 将这种改进的 CFA 融入到 KHM 中优 化其目标函数,通过对实际数据集的实验可以看出 本文所提的聚类算法能够获得更好的性能指标,有 效抑制了陷入局部最优的问题。 1 算法概念与定义 1.1 K⁃调和均值算法 K⁃调和均值算法的原理基本上与 K⁃means 是相 似的,不同的是其使用调和均值( harmonic means, HM)代替算术均值来计算目标函数,能够有效解决 对初始类中心点选取的敏感性问题。 假定数据集 X =[x1 x2 … xn ] 包含 n 个数据,它们被划分 到 k 个聚类簇,每个簇的中心用 cj(j = 1,2,…,k) 表 示,KHM 的目标函数为[3] KHM(X,C) = ∑ n i = 1 k ∑ k j = 1 1 ‖xi - cj‖p ,∀i = 1,2,…,n (1) 这里采用欧式距离计算样本到聚类中心的 距离,参数 p 对算法的性能具有重要的影响,且 当 p≥2 时聚类的效果比较好[ 2] 。 算法通过不断 地迭代使目标函数值不断减小并保持稳定,每次 迭代过程中,各个簇的中心点 cj( j = 1,2,…,k) 的 更新如下[3] 。 cj new = ∑ n i = 1 mKHM(cj / xi) × wKHM(xi) × xi ∑ n i = 1 mKHM(cj / xi) × wKHM(xi) (2) 式中:成员函数 mKHM和权重函数 wKHM的定义分别为 式(3)和式(4)。 mKHM(cj / xi) = ‖xi - cj‖-p-2 ∑ K j = 1 ‖xi - cj‖ - p - 2 (3) wKHM(xi) = ∑ k j = 1 ‖xi - cj‖-p-2 (∑ k j = 1 ‖xi - cj‖-p ) 2 (4) 1.2 萤火虫算法的相关定义 在 FA 中萤火虫彼此吸引主要取决于 2 个因 素:亮度和吸引度。 亮度决定了个体所处位置的好 坏及其移动方向,吸引度决定了移动的距离,通过亮 度和吸引度的不断更新,实现目标优化。 通常直接 利用目标函数值的大小表示萤火虫 i 的亮度 Ii,即 Ii =f(xi), xi = [xi1 xi2 … xid ] 。 FA 的相关定 义如下[12⁃13] : 定义 1 萤火虫 i 与 j 之间的吸引度为 β = β0 e -γr 2 ij (5) 式中: β0 为在 r = 0 处的吸引度,一般可取值为 1; γ 为光强吸收系数,对算法的性能具有重要的影响,通 常情况下可以取 γ = 1;rij为萤火虫 i 与 j 之间的空 间距离,一般采用欧氏距离计算。 定义 2 萤火虫 i 被更亮的萤火虫 j 吸引而移 动的位置为 xi new = xi + β(xj - xi) + α εi (6) 式中: xi 、 xj 为萤火虫 i 和 j 的位置;α 为步长因子, 可设为常数; εi 为服从均匀分布的随机数向量。 2 基于改进 FA 的 K⁃调和均值聚类 2.1 并行混沌局部搜索策略改进的 FA 基本的 FA 缺乏变异机制,当处于局部极值时 难以摆脱,且当前最优解 xpg 周围是搜索到更优解的 最有利的区域,而 FA 在优化过程中采用对其随机 扰动的方式,搜索效率不高。 混沌优化方法能够有 效地跳出局部最优并搜索到全局最优解,现有文献 第 6 期 朱书伟,等:融合并行混沌萤火虫算法的 K⁃调和均值聚类 ·873·

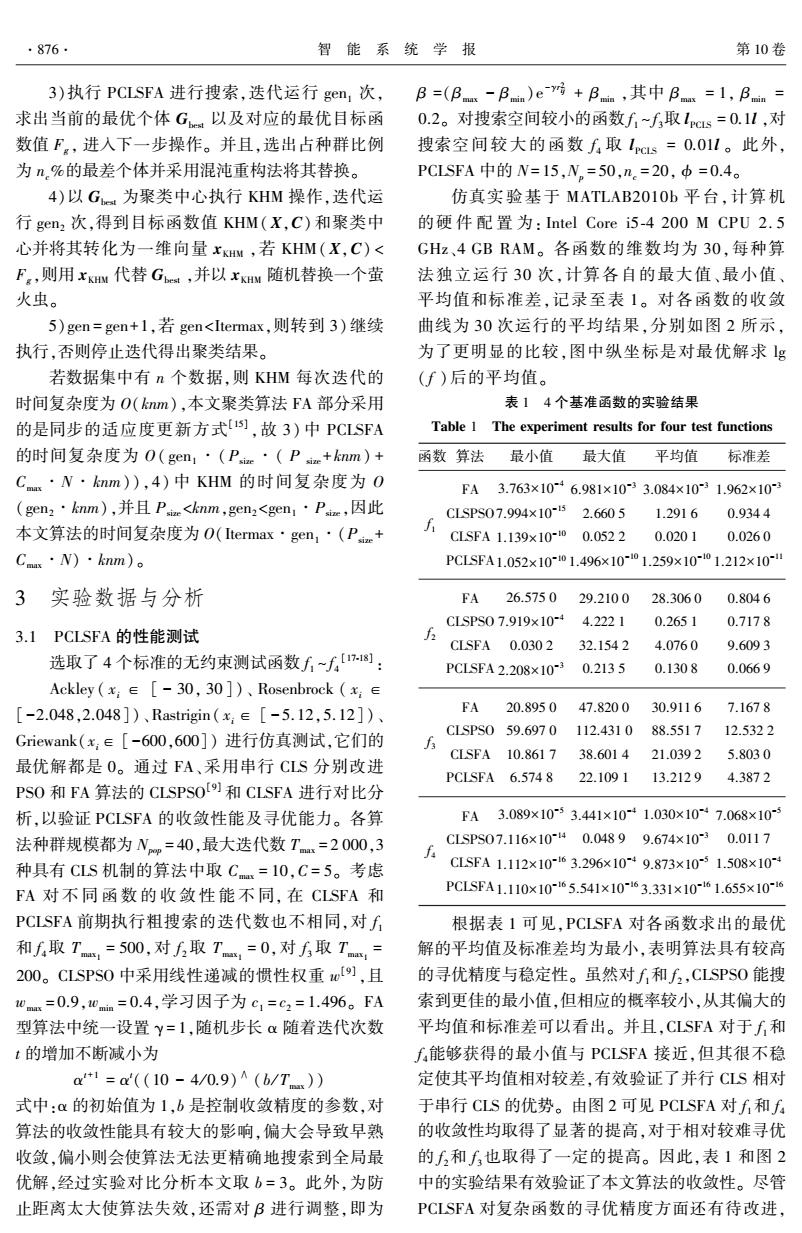
·874… 智能系统学报 第10卷 对混沌模型的研究非常广泛,如logistic映射、Sinu- 1.0 soidal映射、Gaussian映射等16,1。文献[9-10]中采 取一种改进logistic映射分别与粒子群(particle swarm optimization,PS0)算法和差分进化算法融合 提出2种有效的基于CLS的混合优化算法,成功用 于短期梯级水电系统调度问题,并且在文献[19]中 验证了这种混沌映射的优势,它具有较大的李雅普 -1.0 -0.590.51.0 诺夫指数。logistic映射模型为[1例 y(1+1)=4y()(1-y(l)),y(1)∈(0,1) (b)多峰 图12种特殊情况的最优解与次优解局部搜索区域 (7) Fig.1 Two particular types of local search region a- 式中:l表示迭代次数,需要注意的是混沌变量初始 round the best and second best solutions 值y(0){0.25,0.5,0.75},若设置y(1)=(z(l)+ 为了进一步提高搜索效率,提出一种并行混沌 1)/2,则可以获得改进的logistic映射如式(8)1): 局部搜索(parallel chaotic local search,PCLS)策略, z(1+1)=1-2(z(1))2,z(1)∈(-1,1)(8) 采用并行混沌优化的思想产生N个混沌局部变量 并且其概率密度分布表达式为 对次优解和最优解并行扰动,不但克服传统CLS的 1 ,z∈(-1,1) 串行机制搜索精确解效率不高、收敛稳定性不强等 f(z)=m√1-z (9) 缺点[910,还能够有效地兼顾最优解与次优解。当 0,z年(-1,1) 最优解和次优解接近时可将它们的作用视为相等, 由式(9)可以看出改进logistic映射可以将混沌 不接近时则能够有效地拓展局部搜索空间。每次迭 变量的搜索空间拓展到(-1,1),在接近边界-1和1 代后取N个并行变量与xg和x综合排序获得新 处具有较大的概率密度值,因此具有更好的遍历性、 的最优解和次优解,有效地提高算法搜索能力。 随机性。因此,本文利用改进logistic映射在当前最 考虑到文献[17-18]中PC0结合了粗搜索与细 优解附近直接搜索,其本质上属于一种混沌干扰法, 搜索的策略以平衡算法的探索与开发性能,为了使 即产生许多局部最优解的邻域点,以增强搜索到全 并行混沌局部搜索萤火虫算法(parallel chaotic local 局最优解的概率。与此同时,适应度值仅次于最优 search firefly algorithm,PCLSFA)在前期进行一定的 解x的次优解x同样对搜索到更优解具有一定的 粗搜索,可在前T次迭代直接执行FA,PCLSFA 价值,文献[20]中以最优点和次优点为基础进行反 的具体过程为: 射、延伸、收缩等步骤的单纯形法也为本文提供一定 1)初始化萤火虫个体的位置并计算其对应的 的启发。为了更直观地分析,在图1中分别给出二 目标函数值1,作为亮度,初始化迭代次数t=0,最大 维的单峰和多峰搜索空间的2种特殊情况的次优解 迭代次数设为T,粗搜索迭代次数T1o 与最优解局部搜索区域,它们的局部搜索半径均相 2)执行FA不断更新亮度,最亮的个体即为当 等,并且假定越往内适应度值越好。从图1(a)、 前最优解xs,并且次优解为x,若>T1,则采用 (b)中可见2种特殊情况下次优解相对于最优解均 PCLS在它们附近寻优作为细搜索。 具有更好的搜索潜力。 3)设置当前混沌搜索次数1=0,在上文几个断 点外的区域初始化混沌变量-1<g<1(i=1,2, 1.0 饮优解 …,N;j=1,2,…,m),N为并行变量数,m为单变量 0.5 维数,则表示第i个并行变量的第j维。此外,中 最秋解 间变量矩阵为Y,PCLS最大迭代次数为Cr。 ①考虑到大多数情况下x具有更好的搜索潜 -0.5 力,令0=n(,i=1,2…2,且0=.(0. -1.0 0.5 0 0.51.0 i=2N+12W+2 3 ,3,,N,使用式(8)确定第41次 (a)单峰 迭代的混沌扰动变量写+
对混沌模型的研究非常广泛,如 logistic 映射、Sinu⁃ soidal 映射、Gaussian 映射等[16,19] 。 文献[9⁃10]中采 取一种 改 进 logistic 映 射 分 别 与 粒 子 群 ( particle swarm optimization, PSO)算法和差分进化算法融合 提出 2 种有效的基于 CLS 的混合优化算法,成功用 于短期梯级水电系统调度问题,并且在文献[19]中 验证了这种混沌映射的优势,它具有较大的李雅普 诺夫指数。 logistic 映射模型为[19] y(l + 1) = 4y(l)(1 - y(l)), y(l) ∈ (0,1) (7) 式中:l 表示迭代次数,需要注意的是混沌变量初始 值 y(0) ∉ {0.25,0.5,0.75} ,若设置 y(l) = (z(l) + 1) / 2,则可以获得改进的 logistic 映射如式(8) [19] : z(l + 1) = 1 - 2 (z(l)) 2 ,z(l) ∈ ( - 1,1) (8) 并且其概率密度分布表达式为 f(z) = 1 π 1 - z 2 ,z ∈ ( - 1,1) 0,z ∉ ( - 1,1) ì î í ï ï ïï (9) 由式(9)可以看出改进 logistic 映射可以将混沌 变量的搜索空间拓展到(-1,1),在接近边界-1 和 1 处具有较大的概率密度值,因此具有更好的遍历性、 随机性。 因此,本文利用改进 logistic 映射在当前最 优解附近直接搜索,其本质上属于一种混沌干扰法, 即产生许多局部最优解的邻域点,以增强搜索到全 局最优解的概率。 与此同时,适应度值仅次于最优 解 xpg 的次优解 xps 同样对搜索到更优解具有一定的 价值,文献[20]中以最优点和次优点为基础进行反 射、延伸、收缩等步骤的单纯形法也为本文提供一定 的启发。 为了更直观地分析,在图 1 中分别给出二 维的单峰和多峰搜索空间的 2 种特殊情况的次优解 与最优解局部搜索区域,它们的局部搜索半径均相 等,并且假定越往内适应度值越好。 从图 1 ( a)、 (b)中可见 2 种特殊情况下次优解相对于最优解均 具有更好的搜索潜力。 (a)单峰 (b)多峰 图 1 2 种特殊情况的最优解与次优解局部搜索区域 Fig.1 Two particular types of local search region a⁃ round the best and second best solutions 为了进一步提高搜索效率,提出一种并行混沌 局部搜索(parallel chaotic local search, PCLS)策略, 采用并行混沌优化的思想产生 N 个混沌局部变量 对次优解和最优解并行扰动,不但克服传统 CLS 的 串行机制搜索精确解效率不高、收敛稳定性不强等 缺点[9⁃10] ,还能够有效地兼顾最优解与次优解。 当 最优解和次优解接近时可将它们的作用视为相等, 不接近时则能够有效地拓展局部搜索空间。 每次迭 代后取 N 个并行变量与 xpg 和 xps 综合排序获得新 的最优解和次优解,有效地提高算法搜索能力。 考虑到文献[17⁃18]中 PCO 结合了粗搜索与细 搜索的策略以平衡算法的探索与开发性能,为了使 并行混沌局部搜索萤火虫算法(parallel chaotic local search firefly algorithm, PCLSFA)在前期进行一定的 粗搜索,可在前 Tmax1 次迭代直接执行 FA,PCLSFA 的具体过程为: 1)初始化萤火虫个体的位置并计算其对应的 目标函数值 Ii作为亮度,初始化迭代次数 t = 0,最大 迭代次数设为 Tmax,粗搜索迭代次数 Tmax1 。 2)执行 FA 不断更新亮度,最亮的个体即为当 前最优解 xpg ,并且次优解为 xps ,若 t>Tmax1 ,则采用 PCLS 在它们附近寻优作为细搜索。 3)设置当前混沌搜索次数 l = 0,在上文几个断 点外的区域初始化混沌变量-1<zij (0) <1 ( i = 1,2, …,N; j = 1,2,…,m),N 为并行变量数,m 为单变量 维数,则 zij表示第 i 个并行变量的第 j 维。 此外,中 间变量矩阵为 Y ,PCLS 最大迭代次数为 Cmax。 ①考虑到大多数情况下 xpg 具有更好的搜索潜 力,令 y (l) i = xpg (l) , i = 1,2…, 2N 3 ,且 y (l) i = xps (l), i = 2N + 1 3 , 2N + 2 3 ,…,N ,使用式(8)确定第 l+1 次 迭代的混沌扰动变量 zij ( l+ 1) 。 ·874· 智 能 系 统 学 报 第 10 卷

第6期 朱书伟,等:融合并行混沌莹火虫算法的K-调和均值聚类 ·875· ②混沌变量与收缩因子B,成比例,通过混沌扰 式(15)所示,获得替换种群并更新其适应度值。 动产生N个新变量如式(10)所示。 x"M=b+Cx;(b-a) (15) y)=y(+B(Iras (10) 这里随着迭代次数的增加对边界范围不断收 式中:lrs为并行混沌局部搜索的范围,可将其设 缩,在各个不同阶段生成不同尺度的混沌变量,能够 置为0.01l~0.11,1为变量尺度,若6、l分别为变 避免直接根据初始的定义域随机生成替代个体时效 量的上下界,则取1=(u,-1,)/2,收缩因子B,为 率不高的问题,且同样能够改善种群多样性。 B=e-cvTn (11) 2.3改进FA的收敛性分析及复杂度分析 式中:C是一个用于控制PCLS精度的正数,根据实 目前,FA还没有很完备的数学理论基础[2),但 验分析可在[1,10]内选取,一般对于较难搜索到全 已有的仿真实验结果表明FA具有较高的寻优精度 局最优的问题取较小值。求得N个新变量组成的 和收敛速度,是一种有效的优化方法。本文改进算法 矩阵为 与基本FA的不同之处为迭代T,次后增加了PCLS (1+1) y11 2+) …yw7 过程,故只需证明3)过程的收敛性,即可证明PCLS 31) y2(1 …y2*0 FA的收敛性优于FA。从测度论上进行分析,由于 (12) PCLS属于下降算法,并且它具有很好的遍历性,因而 (1+1) 设R表示全局最优点x·的可行域。总迭代次数为t LYMI 时(t>T,),在执行2)后的当前最优解xg和次优解 ③计算每个新变量所对应的目标函数值为 fy,”),并将y+w与xw”、x+》合并,对这 x落入R的事件集合为A,P(A,)≤1,PCLS每次 N+2个变量的适应度值进行排序,得到第l+1次迭 迭代后产生的序列矩阵y”且与x”、x0(1=1, 代中的最优解x网)和次优解xn。 2,…,C)合并后落入R的事件集合为A,因此AC ④=l+1,若l<C,转向①;否则转向4)。 A,C…CAc,概率测度单调不减,故P(Ac)≥ …≥P(A2)≥P(A)。可知执行3)之后具有更高的 4)t=t+1,若t<Tmx,转向2),且随机选取一个 萤火虫个体用3)中获得的x替换并更新其亮度; 概率落入全局最优点x·的可行域,故PCLSFA的收 敛性优于FA,接下来通过对基准函数的仿真实验能 否则停止迭代,输出全局最优解。 够进一步验证其收敛性。此外,当忽略对目标函数的 2.2提高种群多样性的策略 由于FA缺乏保持种群多样性的操作,降低了 计算时,FA的时间复杂度为O(Ts·N2),且 算法探索到全局最优解的能力,因此需要采取一定 PCLSFA的时间复杂度为O(Tm·Np2+T2· 的措施来解决这一问题。本文中算法每迭代V。次 Cmx·N),(Tnma=Tnax-Tmxi)。 2.4KHM-PCLSFA算法流程 时,找出适应度值最差的n%的个体并采用混沌重 本文采用K-调和均值的目标函数KHM(X,C) 构法生成新的个体替代它们。对于各维尺度相等的 优化问题,直接计算出当前种群所有维空间的最大 作为萤火虫i的亮度1:,并以此确定其移动方向,其 值xmm和最小值xmn作为各维的统一边界。对于各 本质上是将聚类问题转化为一种优化问题。若k为 维尺度不相等的优化问题,对边界向量不断地收缩, 聚类的数量,m为数据的维数,则用一个k×m列的 初始时第j维的边界等于定义域[a,b],当达到第 一维向量x=(x1,x2,…,xm,…,x1,x2,…,xm) 来表示一个聚类中心,即一个萤火虫个体。由于算 N,次迭代的最优个体为x·,根据式(13)收缩边界。 法对初始值不敏感,可从数据集中随机选择k个不 %=考-o(6,-a) (13) 同的点并对其进行较小的扰动以构成一个中心向量 (b"ew=x·+p(b-a) x,确定P个这样的向量作为种群初始位置。由于 式中:p∈(0,0.5),并且为了保证新的边界范围不 本文算法的总迭代次数Itermax较小,不需要执行粗 会越界,对其进行相应的处理为:若a"<a,则 搜索。 g=a;若b,>b,则6=b。然后根据式(7)的 综上所述,本文算法KHM-PCLSFA的流程为: logistic映射生成比例为n.%的N个在(0,1)上的向 1)初始化算法的基本参数y、aB、Cms、N、l并 量Cx(i=1,2,…,N)如式(14)所示。 随机初始化萤火虫种群的位置。 Cx:=4×y×(1-y),y∈(0,1)(14) 2)根据萤火虫的位置计算其目标函数值作为 最后再将其转换到当前种群变量的取值空间如 亮度,初始化当前迭代次数gen=0
②混沌变量与收缩因子 βt 成比例,通过混沌扰 动产生 N 个新变量如式(10)所示。 yij (l+1) = yij (l) + βt zij (l+1) lPCLS (10) 式中: lPCLS 为并行混沌局部搜索的范围,可将其设 置为 0.01l ~0.1l , l 为变量尺度,若 ub 、 l b 分别为变 量的上下界,则取 l = (ub - l b) / 2,收缩因子 βt 为 βt = e -C∗t/ Tmax (11) 式中:C 是一个用于控制 PCLS 精度的正数,根据实 验分析可在[1,10]内选取,一般对于较难搜索到全 局最优的问题取较小值。 求得 N 个新变量组成的 矩阵为 Y (l+1) = y11 (l+1) y12 (l+1) … y1m (l+1) y21 (l+1) y22 (l+1) … y2m (l+1) ︙ ︙ ︙ yN1 (l+1) yN2 (l+1) … yNm (l+1) é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú (12) ③计算每个新变量所对应的目标函数值为 f(yi (l+1) ) ,并将 Y (l+1) 与 xpg (l+1) 、 xps (l+1) 合并,对这 N+2 个变量的适应度值进行排序,得到第l+1 次迭 代中的最优解 xpg (l+1) 和次优解 xps (l+1) 。 ④l = l+1,若 l<Cmax,转向①;否则转向 4)。 4)t = t+1,若 t<Tmax,转向 2),且随机选取一个 萤火虫个体用 3)中获得的 xpg 替换并更新其亮度; 否则停止迭代,输出全局最优解。 2.2 提高种群多样性的策略 由于 FA 缺乏保持种群多样性的操作,降低了 算法探索到全局最优解的能力,因此需要采取一定 的措施来解决这一问题。 本文中算法每迭代 Np次 时,找出适应度值最差的 nc%的个体并采用混沌重 构法生成新的个体替代它们。 对于各维尺度相等的 优化问题,直接计算出当前种群所有维空间的最大 值 xmax和最小值 xmin作为各维的统一边界。 对于各 维尺度不相等的优化问题,对边界向量不断地收缩, 初始时第 j 维的边界等于定义域[aj,bj],当达到第 Np次迭代的最优个体为 x ∗ ,根据式(13)收缩边界。 aj new = xj ∗ - φ(bj - aj) bj new = xj ∗ + φ(bj { - aj) (13) 式中: φ ∈ (0,0.5) ,并且为了保证新的边界范围不 会越界, 对其进行相应的处理为: 若 aj new < aj, 则 aj new = aj;若 bj new >bj,则 bj new = bj。 然后根据式(7)的 logistic 映射生成比例为 nc%的 Nc个在(0,1)上的向 量 Cxi(i = 1,2,…,Nc) 如式(14)所示。 Cxi = 4 × y × (1 - y),y ∈ (0,1) (14) 最后再将其转换到当前种群变量的取值空间如 式(15)所示,获得替换种群并更新其适应度值。 xi new = b + Cxi(b - a) (15) 这里随着迭代次数的增加对边界范围不断收 缩,在各个不同阶段生成不同尺度的混沌变量,能够 避免直接根据初始的定义域随机生成替代个体时效 率不高的问题,且同样能够改善种群多样性。 2.3 改进 FA 的收敛性分析及复杂度分析 目前,FA 还没有很完备的数学理论基础[12⁃13] ,但 已有的仿真实验结果表明 FA 具有较高的寻优精度 和收敛速度,是一种有效的优化方法。 本文改进算法 与基本 FA 的不同之处为迭代 Tmax1次后增加了 PCLS 过程,故只需证明 3)过程的收敛性,即可证明 PCLS⁃ FA 的收敛性优于 FA。 从测度论上进行分析,由于 PCLS 属于下降算法,并且它具有很好的遍历性,因而 设 Rg 表示全局最优点 x ∗ 的可行域。 总迭代次数为 t 时(t>Tmax1 ),在执行 2)后的当前最优解 xpg 和次优解 xps 落入 Rg 的事件集合为 A0 , P(A0 ) ≤ 1, PCLS 每次 迭代后产生的序列矩阵 y (l) 且与 xpg (l) 、 xps (l) (l = 1, 2,…,Cmax)合并后落入 Rg 的事件集合为 Al,因此A1⊂ A2⊂ … ⊂ ACmax ,概率测度单调不减,故 P(ACmax ) ≥ … ≥P(A2 ) ≥ P(A1 )。 可知执行 3)之后具有更高的 概率落入全局最优点 x ∗ 的可行域,故 PCLSFA 的收 敛性优于 FA,接下来通过对基准函数的仿真实验能 够进一步验证其收敛性。 此外,当忽略对目标函数的 计算时,FA 的时间复杂度为 O ( Tmax ∙Npop2 ),且 PCLSFA 的时间复杂度为 O( Tmax ∙Npop2 + Tmax 2 ∙ Cmax∙N),(Tmax2 =Tmax -Tmax 1 )。 2.4 KHM⁃PCLSFA 算法流程 本文采用 K⁃调和均值的目标函数 KHM( X,C ) 作为萤火虫 i 的亮度 Ii,并以此确定其移动方向,其 本质上是将聚类问题转化为一种优化问题。 若 k 为 聚类的数量,m 为数据的维数,则用一个 k×m 列的 一维向量 x = (x11 ,x12 ,…,x1m ,…,xk1 ,xk2 ,…,xkm ) 来表示一个聚类中心,即一个萤火虫个体。 由于算 法对初始值不敏感,可从数据集中随机选择 k 个不 同的点并对其进行较小的扰动以构成一个中心向量 x,确定 Psize个这样的向量作为种群初始位置。 由于 本文算法的总迭代次数 Itermax 较小,不需要执行粗 搜索。 综上所述,本文算法 KHM⁃PCLSFA 的流程为: 1)初始化算法的基本参数 γ、 α、β、Cmax、 N、l 并 随机初始化萤火虫种群的位置。 2)根据萤火虫的位置计算其目标函数值作为 亮度,初始化当前迭代次数 gen = 0。 第 6 期 朱书伟,等:融合并行混沌萤火虫算法的 K⁃调和均值聚类 ·875·
·876. 智能系统学报 第10卷 3)执行PCLSFA进行搜索,迭代运行gen,次,B=(B-B)er房+B,其中B=1,Ba= 求出当前的最优个体G以及对应的最优目标函 0.2。对搜索空间较小的函数f1~f取1cs=0.1l,对 数值F,进入下一步操作。并且,选出占种群比例 搜索空间较大的函数f取1cs=0.01l。此外, 为%的最差个体并采用混沌重构法将其替换。 PCLSFA中的N=15,N。=50,n.=20,中=0.4。 4)以G为聚类中心执行KHM操作,迭代运 仿真实验基于MATLAB201Ob平台,计算机 行gen2次,得到目标函数值KHM(X,C)和聚类中 的硬件配置为:Intel Core i5-4200MCPU2.5 心并将其转化为一维向量xKHM,若KHM(X,C)< GHz、4 GB RAM。各函数的维数均为30,每种算 F,则用xKM代替G,并以xKHM随机替换一个萤 法独立运行30次,计算各自的最大值、最小值、 火虫。 平均值和标准差,记录至表1。对各函数的收敛 5)gen=gen+1,若gen<Itermax,则转到3)继续 曲线为30次运行的平均结果,分别如图2所示, 执行,否则停止迭代得出聚类结果。 为了更明显的比较,图中纵坐标是对最优解求g 若数据集中有n个数据,则KHM每次迭代的 (f)后的平均值。 时间复杂度为O(knm),本文聚类算法FA部分采用 表14个基准函数的实验结果 的是同步的适应度更新方式,故3)中PCLSFA Table 1 The experiment results for four test functions 的时间复杂度为O(gen,·(Pic·(Pr+knm)+ 函数算法 最小值 最大值 平均值 标准差 Cms·N·knm),4)中KHM的时间复杂度为O FA3.763×1046.981×10-33.084×1031.962×10 (gen2·knm),并且Pe<khnm,gen,<gen1·Pc,因此 CLSPS07.994×1052.6605 1.2916 0.9344 本文算法的时间复杂度为O(Itermax·gen,·(Pc+ CLSFA1.139x10i00.0522 0.0201 0.0260 Cmax·N)·knm)。 PCLSFA1.052×10-01.496×10-01.259×10~01.212×101 3 实验数据与分析 FA 26.575029.2100 28.3060 0.8046 CLSPS07.919×10-4 4.2221 0.2651 0.7178 3.1 PCLSFA的性能测试 CLSEA 0.0302 32.1542 4.0760 9.6093 选取了4个标准的无约束测试函数f~f): PCLSFA2.208×10-3 0.2135 0.1308 0.0669 Ackley(x:∈[-30,30])、Rosenbrock(x∈ [-2.048,2.048])、Rastrigin(x:∈[-5.12,5.12])、 FA 20.8950 47.8200 30.9116 7.1678 CLSPS059.6970112.431088.5517 12.5322 Griewank(x:∈[-600,600])进行仿真测试,它们的 f CLSFA 10.8617 38.6014 21.0392 5.8030 最优解都是O。通过FA、采用串行CLS分别改进 PCLSFA 6.574 8 22.109113.21294.3872 PS0和FA算法的CLSPSOUS)和CLSFA进行对比分 析,以验证PCLSFA的收敛性能及寻优能力。各算 FA 3.089×1053.441×10+1.030×107.068×10-3 法种群规模都为Nm=40,最大迭代数T=2000,3 CLSPS07.116×1040.04899.674×10-30.0117 种具有CLS机制的算法中取Cmm=10,C=5。考虑 斤C5FA1.112x10-3.296×10-9.873x10-51.508×10 FA对不同函数的收敛性能不同,在CLSFA和 PCLSFA1.110×10165.541×10~63.331×1061.655×10-6 PCLSFA前期执行粗搜索的迭代数也不相同,对f 根据表1可见,PCLSFA对各函数求出的最优 和f取T,=500,对6取T,=0,对取T,= 解的平均值及标准差均为最小,表明算法具有较高 200。CLSPS0中采用线性递减的惯性权重w),且 的寻优精度与稳定性。虽然对f和f,CLSPS0能搜 wmm=0.9,0mi=0.4,学习因子为c1=c2=1.496。FA 索到更佳的最小值,但相应的概率较小,从其偏大的 型算法中统一设置y=1,随机步长α随着迭代次数 平均值和标准差可以看出。并且,CLSFA对于f和 t的增加不断减小为 f,能够获得的最小值与PCLSFA接近,但其很不稳 a+1=a((10-4/0.9)A(b/T)) 定使其平均值相对较差,有效验证了并行CLS相对 式中:a的初始值为1,b是控制收敛精度的参数,对 于串行CLS的优势。由图2可见PCLSFA对f和f 算法的收敛性能具有较大的影响,偏大会导致早熟 的收敛性均取得了显著的提高,对于相对较难寻优 收敛,偏小则会使算法无法更精确地搜索到全局最 的f2和f也取得了一定的提高。因此,表1和图2 优解,经过实验对比分析本文取b=3。此外,为防 中的实验结果有效验证了本文算法的收敛性。尽管 止距离太大使算法失效,还需对B进行调整,即为 PCLSFA对复杂函数的寻优精度方面还有待改进
3)执行 PCLSFA 进行搜索,迭代运行 gen1 次, 求出当前的最优个体 Gbest 以及对应的最优目标函 数值 Fg , 进入下一步操作。 并且,选出占种群比例 为 nc%的最差个体并采用混沌重构法将其替换。 4)以 Gbest 为聚类中心执行 KHM 操作,迭代运 行 gen2 次,得到目标函数值 KHM(X,C) 和聚类中 心并将其转化为一维向量 xKHM ,若 KHM(X,C) < Fg ,则用 xKHM 代替 Gbest ,并以 xKHM 随机替换一个萤 火虫。 5)gen = gen+1,若 gen<Itermax,则转到 3)继续 执行,否则停止迭代得出聚类结果。 若数据集中有 n 个数据,则 KHM 每次迭代的 时间复杂度为 O(knm),本文聚类算法 FA 部分采用 的是同步的适应度更新方式[15] ,故 3) 中 PCLSFA 的时间复杂度为 O( gen1 ∙(Psize ∙( P size +knm) + Cmax∙N∙knm)),4) 中 KHM 的时间复杂度为 O (gen2∙knm),并且 Psize<knm,gen2<gen1∙Psize,因此 本文算法的时间复杂度为 O(Itermax∙gen1∙(Psize + Cmax∙N)∙knm)。 3 实验数据与分析 3.1 PCLSFA 的性能测试 选取了 4 个标准的无约束测试函数 f 1 ~ f 4 [17⁃18] : Ackley ( xi ∈ [ - 30, 30 ])、 Rosenbrock ( xi ∈ [-2.048,2.048])、Rastrigin( xi ∈ [ - 5. 12,5. 12])、 Griewank(xi∈ [-600,600]) 进行仿真测试,它们的 最优解都是 0。 通过 FA、采用串行 CLS 分别改进 PSO 和 FA 算法的 CLSPSO [9] 和 CLSFA 进行对比分 析,以验证 PCLSFA 的收敛性能及寻优能力。 各算 法种群规模都为 Npop = 40,最大迭代数 Tmax = 2 000,3 种具有 CLS 机制的算法中取 Cmax = 10,C = 5。 考虑 FA 对 不 同 函 数 的 收 敛 性 能 不 同, 在 CLSFA 和 PCLSFA 前期执行粗搜索的迭代数也不相同,对 f 1 和 f 4取 Tmax1 = 500,对 f 2 取 Tmax1 = 0,对 f 3 取 Tmax1 = 200。 CLSPSO 中采用线性递减的惯性权重 w [9] ,且 wmax = 0.9,wmin = 0.4,学习因子为 c1 = c2 = 1.496。 FA 型算法中统一设置 γ = 1,随机步长 α 随着迭代次数 t 的增加不断减小为 α t+1 = α t ((10 - 4 / 0.9) ∧ (b / Tmax)) 式中:α 的初始值为 1,b 是控制收敛精度的参数,对 算法的收敛性能具有较大的影响,偏大会导致早熟 收敛,偏小则会使算法无法更精确地搜索到全局最 优解,经过实验对比分析本文取 b = 3。 此外,为防 止距离太大使算法失效,还需对 β 进行调整,即为 β =(β max - β min )e -γr 2 ij + β min ,其中 β max = 1, β min = 0.2。 对搜索空间较小的函数 f 1 ~ f 3取 lPCLS = 0.1l ,对 搜索空间较大的函数 f 4 取 lPCLS = 0.01l 。 此外, PCLSFA 中的 N= 15,Np = 50,nc = 20, ϕ = 0.4。 仿真实验基于 MATLAB2010b 平台,计算机 的硬 件 配 置 为: Intel Core i5⁃4 200 M CPU 2. 5 GHz、4 GB RAM。 各函数的维数均为 30,每种算 法独立运行 30 次,计算各自的最大值、最小值、 平均值和标准差,记录至表 1。 对各函数的收敛 曲线为 30 次运行的平均结果,分别如图 2 所示, 为了更明显的比较,图中纵坐标是对最优解求 lg ( f )后的平均值。 表 1 4 个基准函数的实验结果 Table 1 The experiment results for four test functions 函数 算法 最小值 最大值 平均值 标准差 f 1 FA CLSPSO CLSFA PCLSFA 3.763×10 -4 7.994×10 -15 1.139×10 -10 1.052×10 -10 6.981×10 -3 2.660 5 0.052 2 1.496×10 -10 3.084×10 -3 1.291 6 0.020 1 1.259×10 -10 1.962×10 -3 0.934 4 0.026 0 1.212×10 -11 f 2 FA CLSPSO CLSFA PCLSFA 26.575 0 7.919×10 -4 0.030 2 2.208×10 -3 29.210 0 4.222 1 32.154 2 0.213 5 28.306 0 0.265 1 4.076 0 0.130 8 0.804 6 0.717 8 9.609 3 0.066 9 f 3 FA CLSPSO CLSFA PCLSFA 20.895 0 59.697 0 10.861 7 6.574 8 47.820 0 112.431 0 38.601 4 22.109 1 30.911 6 88.551 7 21.039 2 13.212 9 7.167 8 12.532 2 5.803 0 4.387 2 f 4 FA CLSPSO CLSFA PCLSFA 3.089×10 -5 7.116×10 -14 1.112×10 -16 1.110×10 -16 3.441×10 -4 0.048 9 3.296×10 -4 5.541×10 -16 1.030×10 -4 9.674×10 -3 9.873×10 -5 3.331×10 -16 7.068×10 -5 0.011 7 1.508×10 -4 1.655×10 -16 根据表 1 可见,PCLSFA 对各函数求出的最优 解的平均值及标准差均为最小,表明算法具有较高 的寻优精度与稳定性。 虽然对 f 1和 f 2 ,CLSPSO 能搜 索到更佳的最小值,但相应的概率较小,从其偏大的 平均值和标准差可以看出。 并且,CLSFA 对于 f 1和 f 4能够获得的最小值与 PCLSFA 接近,但其很不稳 定使其平均值相对较差,有效验证了并行 CLS 相对 于串行 CLS 的优势。 由图 2 可见 PCLSFA 对 f 1和 f 4 的收敛性均取得了显著的提高,对于相对较难寻优 的 f 2和 f 3也取得了一定的提高。 因此,表 1 和图 2 中的实验结果有效验证了本文算法的收敛性。 尽管 PCLSFA 对复杂函数的寻优精度方面还有待改进, ·876· 智 能 系 统 学 报 第 10 卷