
4.2函数依赖 第4章 4.2.2函数依赖的逻辑蕴涵定义 定义4.2 设F是在关系模式R(U)上成立的函数依赖集合,X,是属性集U的子集, X-→Y是一个函数依赖。如果从F中能够推导出X→Y,即如果对于R的每个满 足F的关系也满足X→Y,则称X→Y为F的逻辑蕴涵(或F逻辑蕴涵X→Y), 记为F=X→Y。 定义4.3 设F是函数依赖集,被逻辑蕴涵的函数依赖的全体构成的集合,称为函数 依赖集F的闭包(Closure),记为F+。即:F+={X→Y)F=X→W
第1章 绪论 11 定义4.2 4.2 函数依赖 第4章 4.2.2 函数依赖的逻辑蕴涵定义 设F是在关系模式R(U)上成立的函数依赖集合,X,Y是属性集U的子集, X→Y是一个函数依赖。如果从F中能够推导出X→Y,即如果对于R的每个满 足F的关系r也满足X→Y,则称X→Y为F的逻辑蕴涵(或F逻辑蕴涵X→Y), 记为F|=X→Y 。 定义4.3 设F是函数依赖集,被F逻辑蕴涵的函数依赖的全体构成的集合,称为函数 依赖集F的闭包(Closure),记为F +。即:F +={ X→Y | F|=X→Y}

4.2函数依赖 第4章 4.2.3函数依赖的推理规则及正确性 自反律Reflexivity) 如果Y二XCU,则X→Y在R上成立 增广律(Augmentation) 若X→Y在R上成立,且ZU,则KZ→YZ在R上也成立 传递律(Transitivity) 若X-→Y和Y→Z在R上成立,则X→Z在R上也成立 定理:如果X→Y是从F用Armstrong?公理推理导出,那么X-→Y在F+中
第1章 绪论 12 若X→Y和Y→Z在R上成立,则X→Z在R上也成立 4.2 函数依赖 第4章 如果Y X U,则X→Y在R上成立 若X→Y在R上成立,且Z U,则XZ→YZ在R上也成立 传递律(Transitivity) 定理:如果X →Y是从F用Armstrong公理推理导出,那么X →Y在F+中。 4.2.3 函数依赖的推理规则及正确性 自反律(Reflexivity) 增广律(Augmentation)
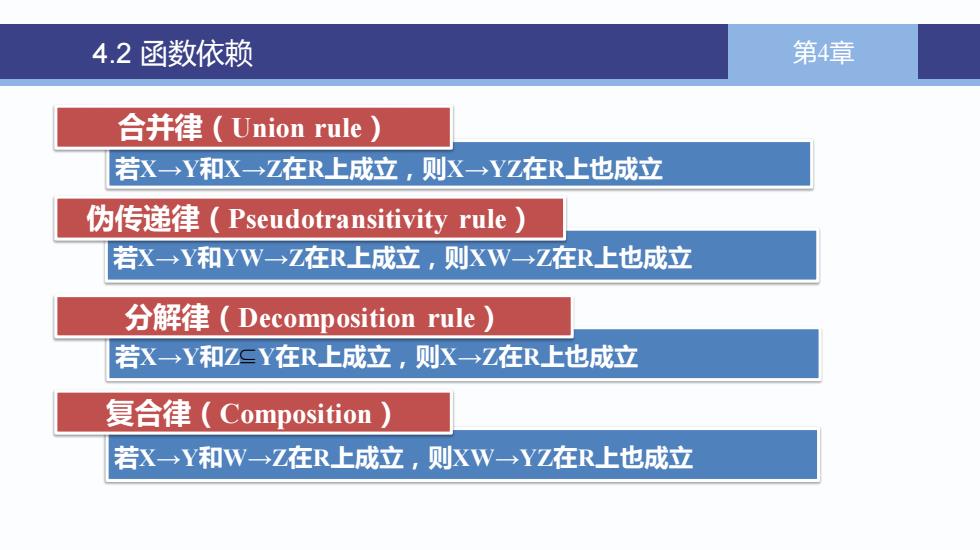
4.2函数依赖 第4章 合并律(Union rule) 若X→Y和X→Z在R上成立,则X→YZ在R上也成立 伪传递律(Pseudotransitivity rule) 若X→Y和YW→Z在R上成立,则XW→Z在R上也成立 分解律(Decomposition rule) 若X→Y和ZSY在R上成立,则K→Z在R上也成立 复合律(Composition) 若X→Y和W→Z在R上成立,则XW→YZ在R上也成立
第1章 绪论 13 若X→Y和W→Z在R上成立,则XW→YZ在R上也成立 若X→Y和Z Y在R上成立,则X→Z在R上也成立 4.2 函数依赖 第4章 若X→Y和X→Z在R上成立,则X→YZ在R上也成立 合并律(Union rule) 若X→Y和YW→Z在R上成立,则XW→Z在R上也成立 分解律(Decomposition rule) 复合律(Composition) 伪传递律(Pseudotransitivity rule)

4.2函数依赖 第4章 4.2.4完全函数依赖与部分函数依赖 定义4.4 设有关系模式R(U),U是属性全集,和Y是的子集: 口如果X→Y,并目对于的任何一个真子集X,都有X叫Y,则称对X完全函数 依赖,记作X玉了。 口如果对的某个真子集X,有X'一Y,则称对部分函数依赖,记作X卫Y。 关系模式SCD中,因为SNo今Score,且CNo Score,所以有:(SNo,CNo fScore。而SNo-→Age,所以(SNo,CNo)BAge。 只有当决定因素是组合属性时,讨论部分函数依赖才有意义; 当决定因素是单属性时,只能是完全函数依赖
第1章 绪论 第 14 4.2 函数依赖 4章 4.2.4 完全函数依赖与部分函数依赖 定义4.4 设有关系模式R(U),U是属性全集,X和Y是U的子集: ❑如果X→Y,并且对于X的任何一个真子集X′,都有X′ Y,则称Y对X完全函数 依赖,记作X → Y。 ❑如果对X的某个真子集X′,有X ′→Y,则称Y对X部分函数依赖,记作X → Y。 关系模式SCD中,因为SNo Score,且CNo Score,所以有:(SNo,CNo) →f Score。而SNo→Age,所以(SNo,CNo) →p Age 。 只有当决定因素是组合属性时,讨论部分函数依赖才有意义; 当决定因素是单属性时,只能是完全函数依赖。 f p

4.2函数依赖 第4章 4.2.5传递函数依赖 定义4.5 设有关系模式R(U,U是属性全集,X,Y,Z是U的子集 ▣ 若X→Y,但X,而Y-→Z(YX,ZY),则称Z对X传递函数依赖 记作:X→Z。 如果Y→X,则X→Y,这时称Z对X直接函数依赖,而不是传递函数依赖。 例如,在关系模式SCD中,SNo→Dept,但Dept+SNo,而Dept→MN,则有SMNo·→MN: 当学生不存在重名的情祝下,有SNo-→SN,SN-→SMNo,SNo台SN,SN一→Dept,这时Depl 付SNo是直接函数依赖,而不是传递函数依赖
第1章 绪论 第 15 4.2 函数依赖 4章 4.2.5 传递函数依赖 定义4.5 设有关系模式R(U),U是属性全集,X,Y,Z是U的子集 ❑ 若X→Y,但Y X,而Y→Z(Y X,Z Y),则称Z对X传递函数依赖 , 记作:X → Z 。 ❑ 如果Y→X,则X Y ,这时称Z对X直接函数依赖,而不是传递函数依赖。