
5.确定P值,推断结论 根据分子U1,分母U22,查F界值表 (方差分析用 表),得到F值的临值(critical value),即: 如果F≥F界值,则P≤0.05,在α=0.05水准上拒 绝Ho接受H1。 结论:可以认为各样本所代表的总体均数不全相等。 如果想要了解哪两个样本均数之间有差异,可以 继续进行各样本均数的两两比较。 简历 返回总目录 返回章目录 结束 第4章方差分析 第20页
简 历 返回总目录 返回章目录 结束 第4章 方差分析 第20页 5. 确定P值,推断结论 根据分子υ1,分母υ2 2,查F界值表(方差分析用 表),得到F值的临界值(critical value),即: 如果F≥F界值,则P≤0.05,在α=0.05水准上拒 绝H0 ,接受H1。 结论:可以认为各样本所代表的总体均数不全相等。 如果想要了解哪两个样本均数之间有差异,可以 继续进行各样本均数的两两比较

第二节单因素方差分折 1. 意义单因素方差分析是按照完全随机设计的原 则将处理因素分为若干个不同的水平,每个水平 代表一个样本,只能分析一个因素对试验结果的 影响及作用。 2.特点:其设计简单,计算方便,应用广泛,是一 种常用的分析方法,但其效率相对较低。该设计 中的总变异可以分出两个部分, SS总=SS组间+SS组内 简历 返回总目录 返回章目录 第4章方差分析 第21页
简 历 返回总目录 返回章目录 结束 第4章 方差分析 第21页 第二节 单因素方差分析 1. 意义 单因素方差分析是按照完全随机设计的原 则将处理因素分为若干个不同的水平,每个水平 代表一个样本,只能分析一个因素对试验结果的 影响及作用。 2. 特点:其设计简单,计算方便,应用广泛,是一 种常用的分析方法,但其效率相对较低。该设计 中的总变异可以分出两个部分, SS总=SS组间+SS组内

3用符号及其意义 X (1)意义为第组的第个数据。其中 下标表示列,表示行。 (2)意义为将第组的全部个数据合 计。 简历 返回总目录 返回章目录口>口结束 第4章方差分析 第22页
简 历 返回总目录 返回章目录 结束 第4章 方差分析 第22页 (1)意义为第i组的第j个数据。其中 下标i表示列,j表示行。 j Xij Xij 3 常用符号及其意义 (2)意义为将第i组的全部j个数据合 计

∑∑X, (3)将第组的个数据合计后平方, j 再将所有各组的平方值合计。 变异来源(单因素) ①SS总:表示变异由处理因素及随机误差共同所致; ② SS组间:表示变异来自处理因素的作用或影响; ③SS组内:表示变异由个体差异和测量误差 等随机因素所致。 简历 返回总目录 返回章目录】口>口结束 第4章方差分析 第23页
简 历 返回总目录 返回章目录 结束 第4章 方差分析 第23页 变异来源(单因素) ① SS总:表示变异由处理因素及随机误差共同所致; ② SS组间:表示变异来自处理因素的作用或影响; ③SS组内:表示变异由个体差异和测量误差 等随机因素所致。 i j Xij 2 ( ) (3) 将第i组的j个数据合计后平方, 再将所有各i组的平方值合计
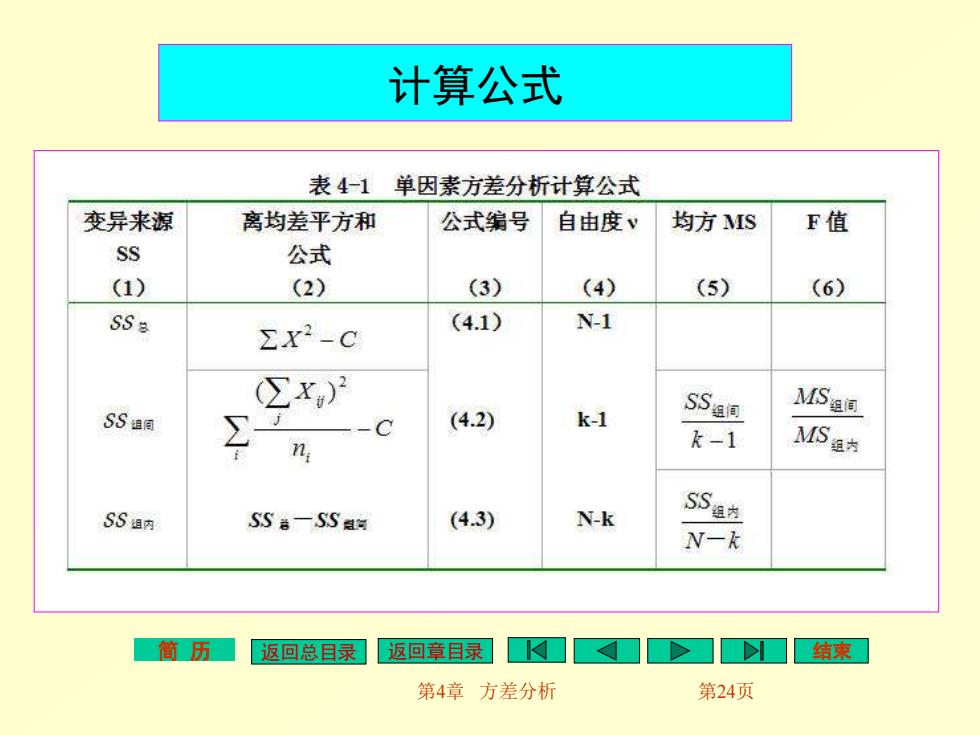
计算公式 表4-1单因素方差分析计算公式 变异来源 离均差平方和 公式编号 自由度v 均方MS F值 SS 公式 (1) (2) (3) (4) (5) (6) SS ∑x2-C (4.1) N-1 ∑x MSa间 SSa间 (4.2) k-1 SS组间 n k-1 MSa为 SS姐内 SS活一SSa (4.3) N-k SSa N-k 简历 返回总目录 返回章目录 第4章方差分析 第24页
简 历 返回总目录 返回章目录 结束 第4章 方差分析 第24页 计算公式