
3. 假设的意义为:在某处理因素的不同水平下,各 样本的总体均数相等。这就意味着处理因素不起 作用。 4.设某因素有多个水平,即试验数据产生多个样本。 由多个样本的全部数据可以计算出总变异,称为 总的离均差平方和。即SS总。 5. 数理统计证明,SS总可以由几个部分构成。单因 素方差分析中,SS总由组间变异和组内变异构 成。SS总=SS组间+SS组内。 简历 返回总目录】 返回章目录 第4章方差分析 第10页
简 历 返回总目录 返回章目录 结束 第4章 方差分析 第10页 3. 假设的意义为:在某处理因素的不同水平下,各 样本的总体均数相等。这就意味着处理因素不起 作用。 4. 设某因素有多个水平,即试验数据产生多个样本。 由多个样本的全部数据可以计算出总变异,称为 总的离均差平方和。即SS总。 5. 数理统计证明,SS总可以由几个部分构成。单因 素方差分析中, SS总由组间变异和组内变异构 成。SS总=SS组间+SS组内

4.组间变异主要受到处理因素和个体误差两方面影 响,组内变异主要受个体误差的影响。当H,为 真时,由于处理因素不起作用,组间变异只受个 体误差的影响。此时,组间变异与组内变异相差 不能太大。两部分的均方(方差)也相差不大。 其比值F值接近1。 5.如果比值远远大于1,如大于3-5倍时,则处理 因素就产生作用,影响了数据的结果。 简历 返回总目录 返回章目录】 第4章方差分析 第11页
简 历 返回总目录 返回章目录 结束 第4章 方差分析 第11页 4. 组间变异主要受到处理因素和个体误差两方面影 响,组内变异主要受个体误差的影响。当H0 为 真时,由于处理因素不起作用,组间变异只受个 体误差的影响。此时,组间变异与组内变异相差 不能太大。两部分的均方(方差)也相差不大。 其比值F值接近1。 5. 如果比值远远大于1 ,如大于3-5倍时,则处理 因素就产生作用,影响了数据的结果
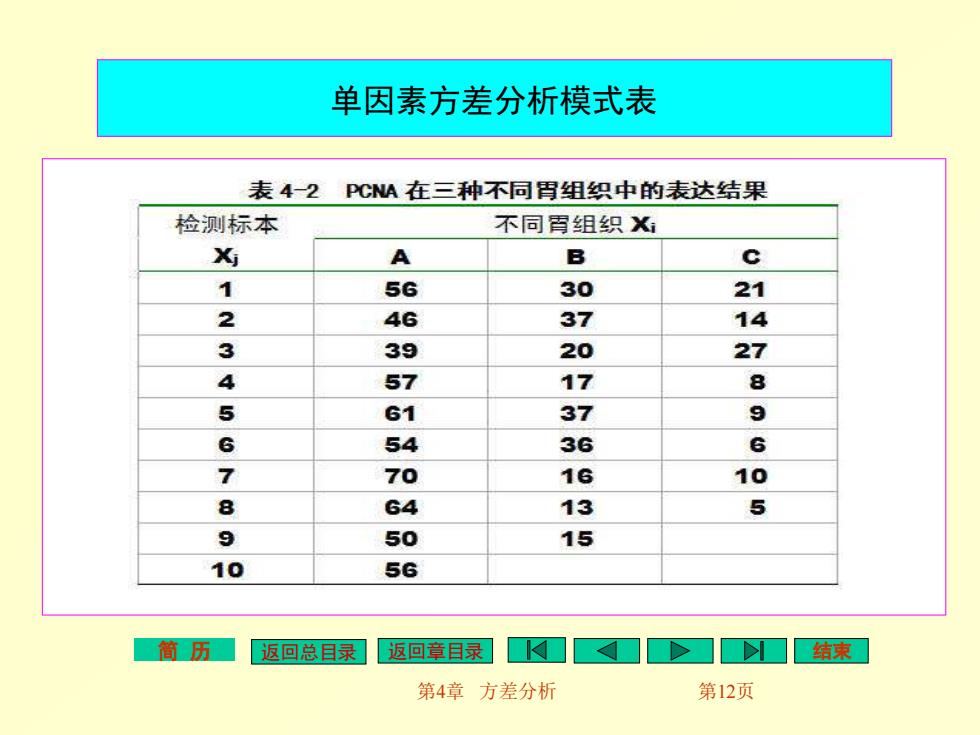
单因素方差分析模式表 表4一2PCA在三种不同胃组织中的表达结果 检测标本 不同霄组织X A B c 1 5G 30 21 2 46 37 14 3 39 20 27 4 57 17 8 5 61 37 9 6 54 36 6 7 70 16 10 8 64 13 5 9 50 15 10 56 简历 返回总目录 返回章目录】 第4章方差分析 第12页
简 历 返回总目录 返回章目录 结束 第4章 方差分析 第12页 单因素方差分析模式表

6. 各种变异除以相应的自由度,称为均方,用MS 表家,也就是方差。当Ho为真时,组间均方与组 内均方相差不大,两者比值F值约接近于1。 即F=组间均方/组内均方≈1。 7. 当H不成立时,处理因素产生了作用,使得组 间均方增大,此时,>>1,当大于等于F临界 值时,则P≤0.05。可认为Ho不成立,各样本均 数不全相等。 简历 返回总目录 返回章目录】 第4章方差分析 第13页
简 历 返回总目录 返回章目录 结束 第4章 方差分析 第13页 6. 各种变异除以相应的自由度,称为均方,用MS 表示,也就是方差。当H0为真时,组间均方与组 内均方相差不大,两者比值F值约接近于1。 即 F=组间均方/组内均方≈1。 7. 当H0不成立时,处理因素产生了作用,使得组 间均方增大,此时,F>>1,当大于等于F临界 值时,则P≤0.05。可认为H0不成立,各样本均 数不全相等

三、方差分析的类型 1.单因素方差分析(one-way ANOVA)也称为完全随 机设计(completely random design)的方差分析。还 可称为单向或单方式方差分析。该设计只能分析一个因 素下多个水平对试验结果的影响。 2.双因素方差分析(two-way ANOVA)称为随机区组 设计(randomized block design)的方差分析。还 可称为双向或双方式方差分析。该设计可以分析两个因 素。一个为处理因素,也称为列因素;一个为区组因素 也称为行因素。 简历 返回总目录 返回章目录 结束 第4章方差分析 第14页
简 历 返回总目录 返回章目录 结束 第4章 方差分析 第14页 1. 单因素方差分析(one-way ANOVA) 也称为完全随 机设计(completely random design)的方差分析。还 可称为单向或单方式方差分析。该设计只能分析一个因 素下多个水平对试验结果的影响。 2. 双因素方差分析(two-way ANOVA) 称为随机区组 设计(randomized block design)的方差分析。还 可称为双向或双方式方差分析。该设计可以分析两个因 素。一个为处理因素,也称为列因素;一个为区组因素, 也称为行因素。 三、方差分析的类型