(2)逻辑函数以一般的逻辑表达式给出:先将函数变换为与或表达式(不 必变换为最小项之和的形式),然后在卡诺图上与每一个乘积项所包含的那 些最小项(该乘积项就是这些最小项的公因子)相对应的方格内填入1,其余 的方格内填入0。 Y=(A+D)(B+C) AD的公因子 达为 AB CD 11 10 武与 00 0 0 Y=AD+BC 0 说明:如果求得了 11 函数Y的反函数Y,则 10 对Y中所包含的各个最 小项,在卡诺图相应方 格内填入0,其余方格内 BC的公因子 填入1
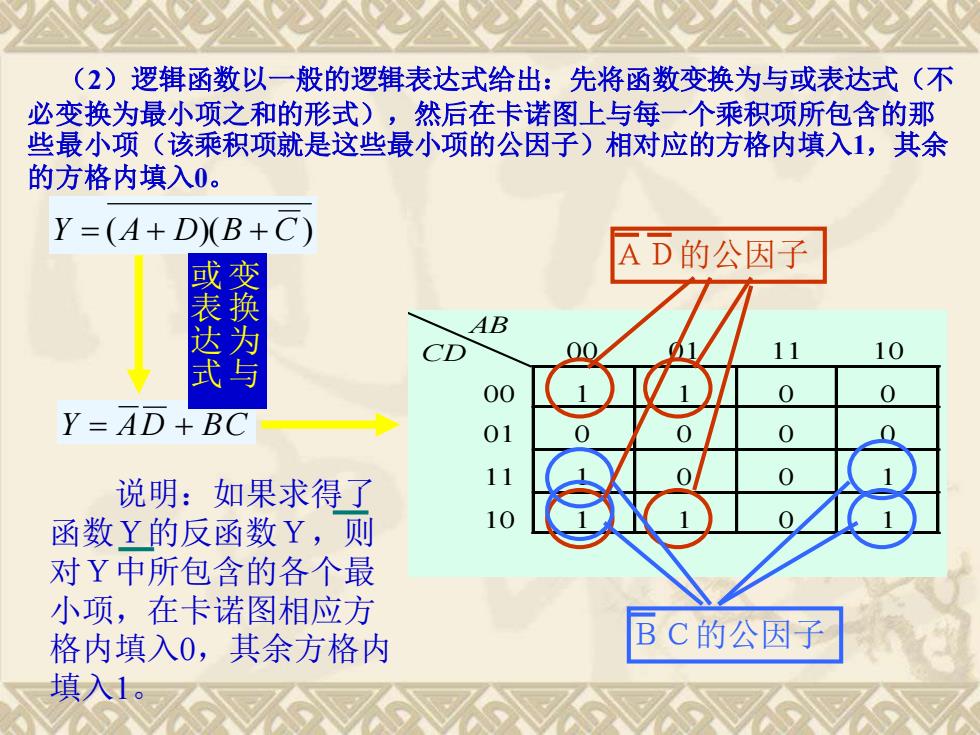
(2)逻辑函数以一般的逻辑表达式给出:先将函数变换为与或表达式(不 必变换为最小项之和的形式),然后在卡诺图上与每一个乘积项所包含的那 些最小项(该乘积项就是这些最小项的公因子)相对应的方格内填入1,其余 的方格内填入0。 Y = (A + D)(B + C) Y = AD + BC AB CD 00 01 11 10 00 1 1 0 0 01 0 0 0 0 11 1 0 0 1 10 1 1 0 1 变 换 为 与 或 表 达 式 AD的公因子 BC的公因子 说明:如果求得了 函数Y的反函数Y,则 对Y中所包含的各个最 小项,在卡诺图相应方 格内填入0,其余方格内 填入1
3、卡诺图的性质 (1)任何两个(2个)标1的相邻最小项,可以合并为一项,并消去一个 变量(消去互为反变量的因子,保留公因子)。 AB 00 01 11 10 0 0 ABC +ABC BC ABC+BC BC AB CD 00 11 10 00 0 1 0 0 01 0 0 0 ABCD+ABCD 11 0 0 0 =ABD 10 0 0 0 ABCD+ABCD =ABD
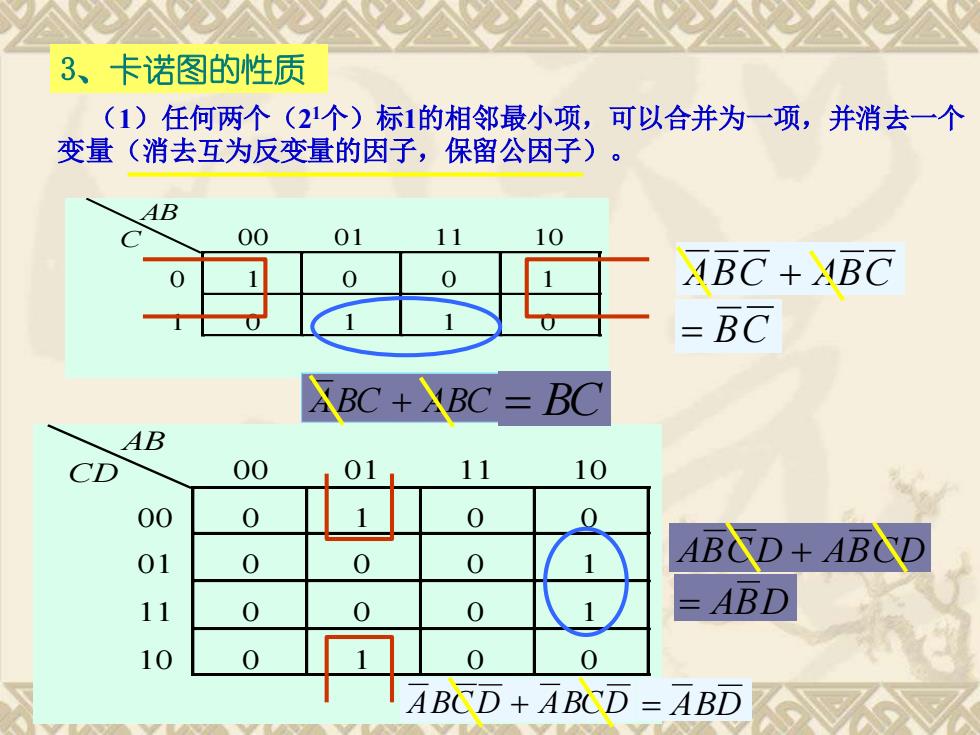
3、卡诺图的性质 AB CD 00 01 11 10 00 0 1 0 0 01 0 0 0 1 11 0 0 0 1 10 0 1 0 0 (1)任何两个(2 1个)标1的相邻最小项,可以合并为一项,并消去一个 变量(消去互为反变量的因子,保留公因子)。 AB C 00 01 11 10 0 1 0 0 1 1 0 1 1 0 ABC + ABC ABC + ABC ABCD + ABCD ABCD + ABCD = BC = BC = ABD = ABD
(2)任何4个(22个)标1的相邻最小项,可以合并为一项 并消去2个变量。 AB C 00 01 10 ABC+ABC ABC ABC 0 =(4B+AB+AB+AB)C 0 0 -C ABC+ABC+ABC+ABC=(AC+AC+AC+AC)B=B AB CD 00 01 11 10 00 0 1 0 0 01 1 1 CD 11 0 1 0 10 0 0 0 AB
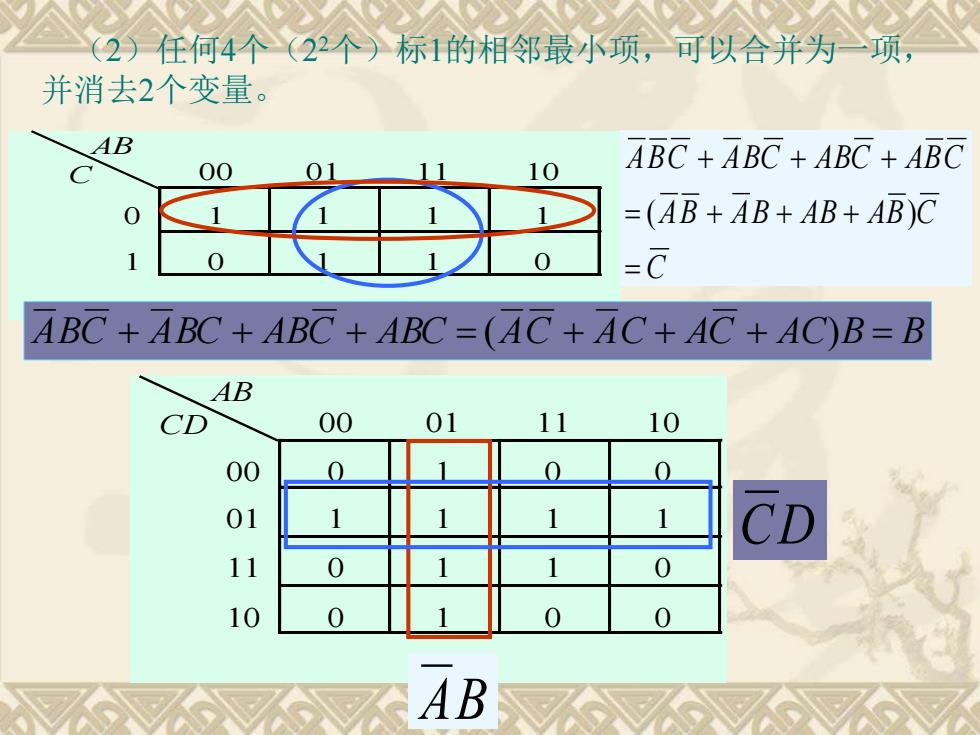
AB CD 00 01 11 10 00 0 1 0 0 01 1 1 1 1 11 0 1 1 0 10 0 1 0 0 (2)任何4个(2 2个)标1的相邻最小项,可以合并为一项, 并消去2个变量。 AB C 00 01 11 10 0 1 1 1 1 1 0 1 1 0 C AB AB AB AB C ABC ABC ABC ABC = = + + + + + + ( ) ABC + ABC + ABC + ABC = (AC + AC + AC + AC)B = B AB CD
AB CD 00 01 00 01 0 0 11 0 BD 10 1 BD AB CD 00 01 11 10 00 1 0 0 01 0 1 1 0 11 0 1 1 0 10 BD BD
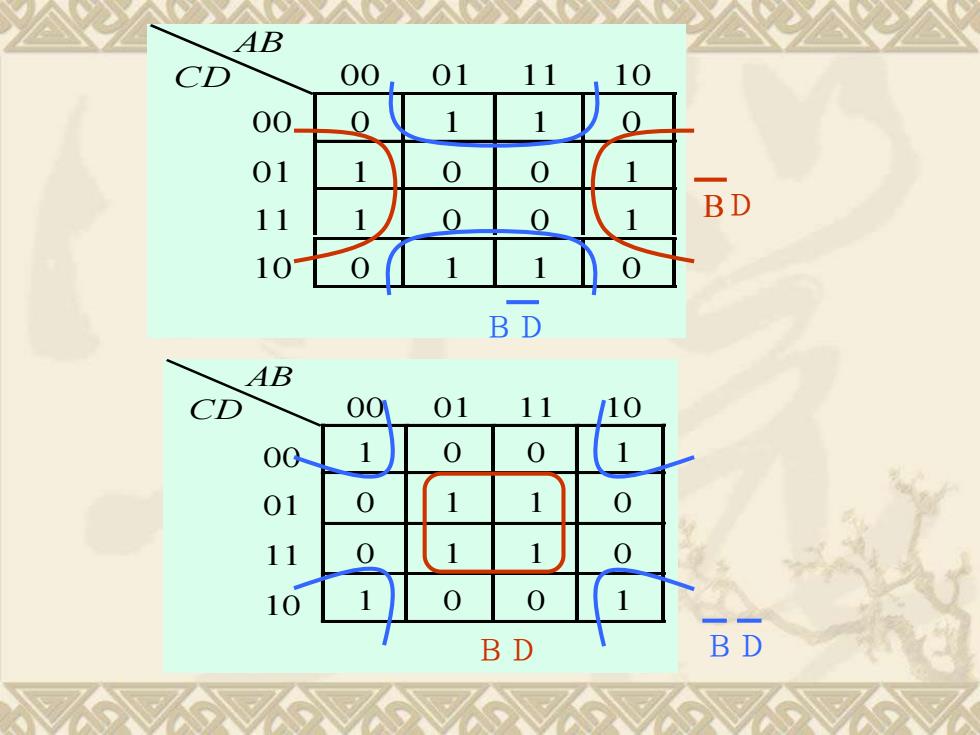
AB CD 00 01 11 10 00 1 0 0 1 01 0 1 1 0 11 0 1 1 0 10 1 0 0 1 AB CD 00 01 11 10 00 0 1 1 0 01 1 0 0 1 11 1 0 0 1 10 0 1 1 0 BD BD BD BD
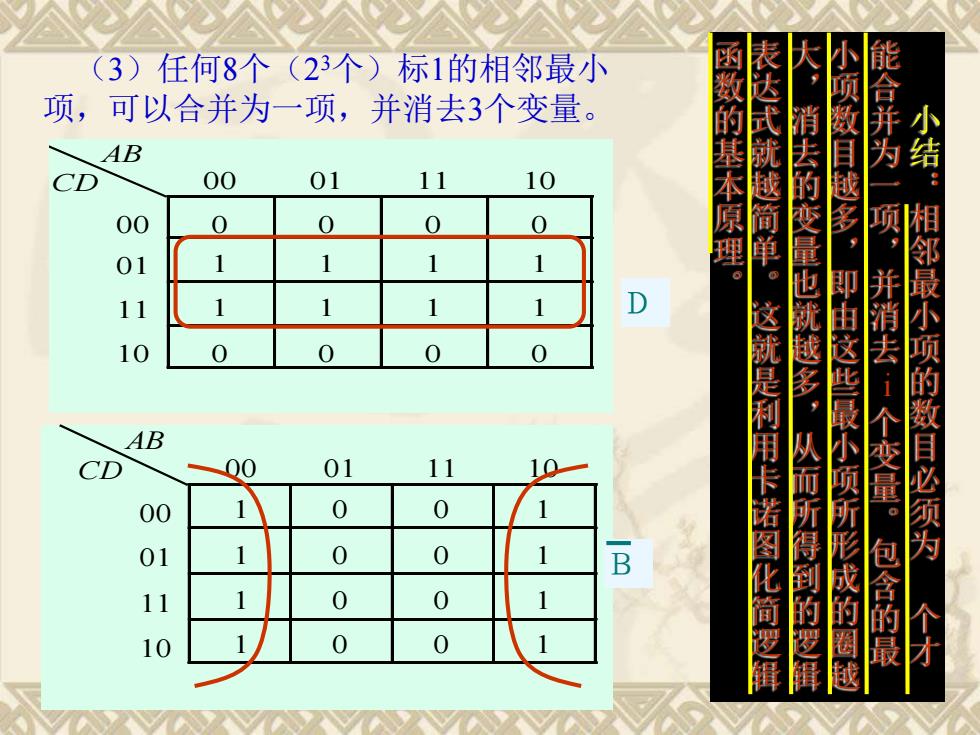
(3)任何8个(23个)标1的相邻最小 大· 项,可以合并为 一项,并消去3个变量。 能合并 AB 函数的基本原 表达式就越简单 小项数目越多, 结 CD 00 01 11 10 00 0 0 0 0 01 1 1 1 1 11 1 1 1 1 D 最小 10 0 0 0 0 并消去 AB CD 00 01 11 00 1 0 0 1 项的数目必须为 01 0 0 B 。这就是利用卡诺图化简逻辑 消去的变量也就越多,从而所得到的逻辑 即由这些最小项所形成的圈 11 0 0 1个变量。包含的最 10 0 0
AB CD 00 01 11 10 00 0 0 0 0 01 1 1 1 1 11 1 1 1 1 10 0 0 0 0 AB CD 00 01 11 10 00 1 0 0 1 01 1 0 0 1 11 1 0 0 1 10 1 0 0 1 (3)任何8个(2 3个)标1的相邻最小 项,可以合并为一项,并消去3个变量。 2 B i 小 结 : 相 邻 最 小 项 的 数 目 必 须 为 个 才 能 合 并 为 一 项 , 并 消 去 个 变 量 。 包 含 的 最 小 项 数 目 越 多 , 即 由 这 些 最 小 项 所 形 成 的 圈 越 大 , 消 去 的 变 量 也 就 越 多 , 从 而 所 得 到 的 逻 辑 表 达 式 就 越 简 单 。 这 就 是 利 用 卡 诺 图 化 简 逻 辑 函 数 的 基 本 原 理 。 D i