1变量卡诺图 变量数n=1在卡诺图上有21=2个 小方格,对应m、m两个最小项。 B 0 0表示A的反变量。 0 AB AB mo 1m2 1表示A的原变量。 A AB AB m 2变量卡诺图 变量数n=2在卡诺图上有22=4个小方格,对应 m0、m1、m2、m3四个最小项。 每个小方格有二个相邻格:m0和m1、m2相邻 B 二变量格雷码排列: 任何相邻码组之间只有一个码元不同。 逻辑相邻,几何位置相邻
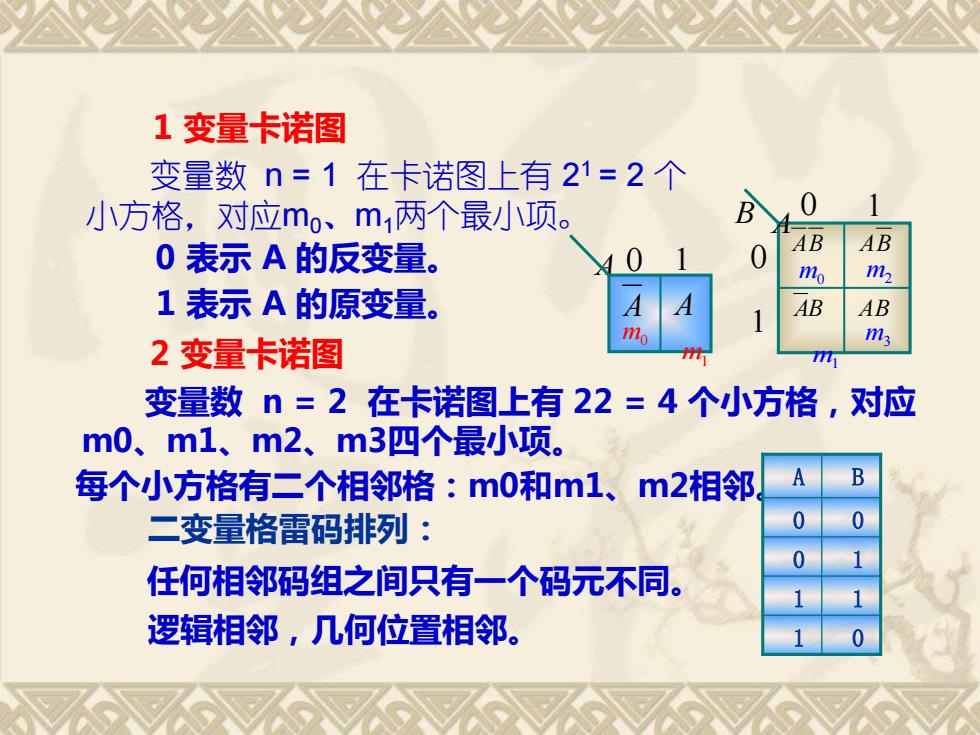
1 变量卡诺图 变量数 n = 1 在卡诺图上有 2 1 = 2 个 小方格,对应m0、m1两个最小项。 0 表示 A 的反变量。 1 表示 A 的原变量。 2 变量卡诺图 变量数 n = 2 在卡诺图上有 22 = 4 个小方格,对应 m0、m1、m2、m3四个最小项。 每个小方格有二个相邻格:m0和m1、m2相邻。A B 0 0 0 1 1 1 1 0 二变量格雷码排列: 任何相邻码组之间只有一个码元不同。 逻辑相邻,几何位置相邻。 A B AB AB AB AB m1 m0 m2 m3 0 1 0 1 A 0 1 m0 m1 A A
3变量卡诺图 AB 变量数n=3在卡诺图上 C 00 01 11 19 4B ABC ABC AB 有23=8个小方格,对应八个最0 m 10 每个小方格有三个相邻格。 ABC ABO AB m mo和m1、m2、m4相令邻。 B m1和mo、m3、m5相邻。 0 0 m2和m0、m3、m6相邻。 ☆小方格的编号就是最划小项的编号。 ☆卡诺图小方格相邻数=变量数。 ☆ 逻辑相邻,几何位置也相邻。 三变量格雷码排列顺序: 要求掌握格雷码排列规律
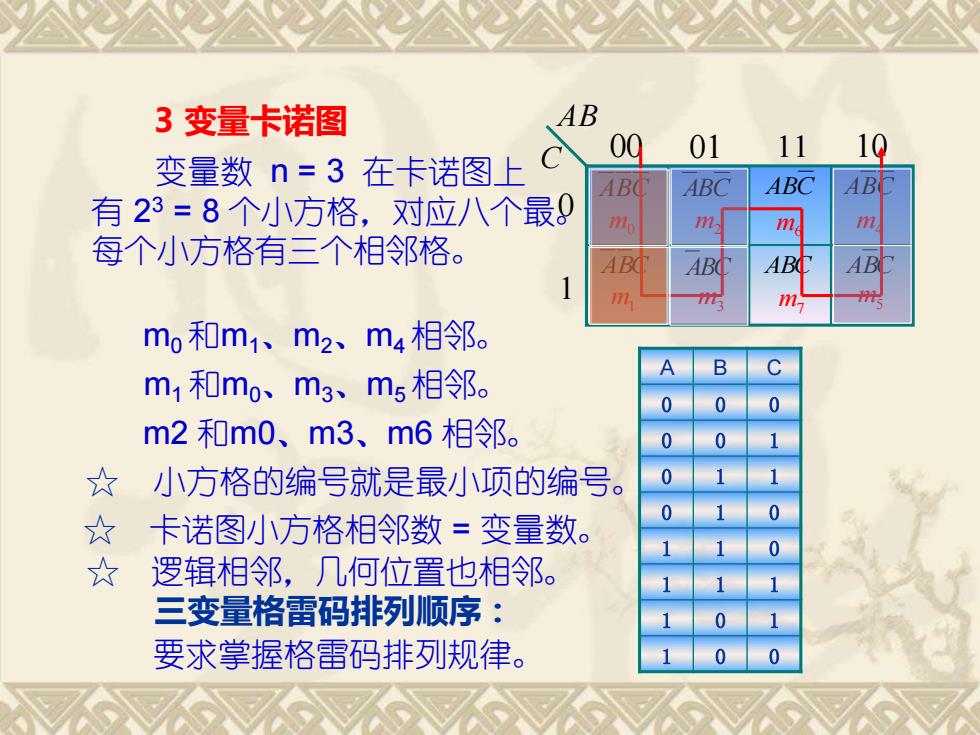
AB C 00 01 11 10 1 0 ABC ABC ABC ABC ABC ABC ABC ABC m0 m2 m1 m3 m4 m5 m6 m7 A B C 0 0 0 0 0 1 0 1 1 0 1 0 1 1 0 1 1 1 1 0 1 1 0 0 3 变量卡诺图 变量数 n = 3 在卡诺图上 有 2 3 = 8 个小方格,对应八个最。 每个小方格有三个相邻格。 m0 和m1、m2、m4 相邻。 m1 和m0、m3、m5 相邻。 m2 和m0、m3、m6 相邻。 三变量格雷码排列顺序: ☆ 卡诺图小方格相邻数 = 变量数。 ☆ 小方格的编号就是最小项的编号。 ☆ 逻辑相邻,几何位置也相邻。 要求掌握格雷码排列规律
4变量卡诺图 AB A A 变量数n=4在卡诺图上有 24=16个小方格,对应十六个 7 最小项。每个小方格有四个相邻 格。 mo和m1、m2、m4、m3相邻。 BCD ABCD.ABCD ABCD 1i5 m5和m1、m4、m7、m13相邻. BCD ABC D.ABC DABCD mg和m1、m3、m11、m13相邻。 77 7 四变量格雷码排列: 0
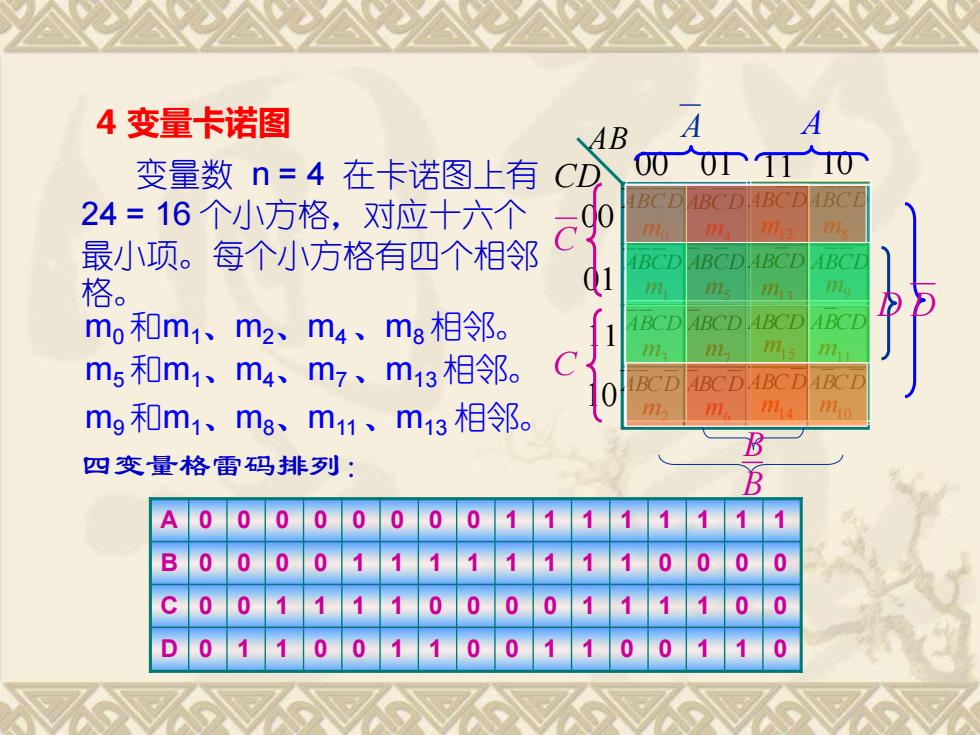
AB CD 00 01 11 10 00011110 ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD m0 m1 m2 m3 m4 m5 m7 m6 m8 m9 m11 m10 m12 m13 m15 m14 4 变量卡诺图 变量数 n = 4 在卡诺图上有 24 = 16 个小方格,对应十六个 最小项。每个小方格有四个相邻 格。 m0 和m1、m2、m4 、m8 相邻。 m5 和m1、m4、m7 、m13 相邻。 m9 和m1、m8、m11 、m13 相邻。 四变量格雷码排列: A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 B 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 C 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 D 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 A A C C B B D D

5变量卡诺图 000 001 011010 110111101100 变量数n=5在卡诺图 m m 12 m s 11n241n281m2o1m6 上有25=32个小方格,对 m ms m is m9 1251m29m27m7 应32个最划小项。每个小方格 有5个相邻格。 1机3 11n ms1mu7仇27 1m317m231机9 m2 1m61m41mo7m261m301l221m8 mo和m1、m2、m4、mg、 及对称相m16° m5和m1、m4、m7、m13、及对称相m21。 找相邻格的方法: 先按四变找 m23和m1g、m21、m22、m31、及对称相m7 再找对称相 m27和m25、m26、m1g、m31、及对称相m110 随着输入变量的增加,小方格数以2n倍增加。若 N=6有64个小方格,使卡诺图变得十分复杂,相邻关系 难以寻找。所以卡诺图一般多用于5变量以内
000 001 011 010 0 0 0 1 1 1 1 0 ABC DE 110 111 101 100 m 0 m 1 m 4 m 5 m 12 m 13 m 8 m 9 m 24 m 25 m 28 m 29 m 7 m 15 m 11 m 27 m 31 m 20 m 16 m 21 m 17 m 23 m 19 m 6 m 14 m 10 m 26 m 30 m 22 m 18 m 3 m 2 5 变量卡诺图 变量数 n = 5 在卡诺图 上有 2 5 = 32 个小方格,对 应32个最小项。每个小方格 有5个相邻格。 m0和m1、m2、m4、m8 、及对称相 m16。 m5和m1、m4、m7、m13 、及对称相 m21。 m23和m19、m21、m22、m31 、及对称相 m7。 m27和m25、m26、m19、m31 、及对称相 m11。 找相邻格的方法: 先按四变找 再找对称相 随着输入变量的增加,小方格数以 2 n 倍增加。若 N=6 有 64个小方格,使卡诺图变得十分复杂,相邻关系 难以寻找。所以卡诺图一般多用于5变量以内
2、逻辑函数在卡诺图中的表示 (1)逻辑函数是以真值表或者以最小项表达式给出:在卡诺图上那些与 给定逻辑函数的最小项相对应的方格内填入1,其余的方格内填入0。 Y(AB,C,D)=∑m1,3,4,6,7,11,14,15) AB CD 00 01 11 10 00 0 m4 m1← OT 1 0 0 0 m3 ← 1士 1 1 m11 10 0 0 m m14
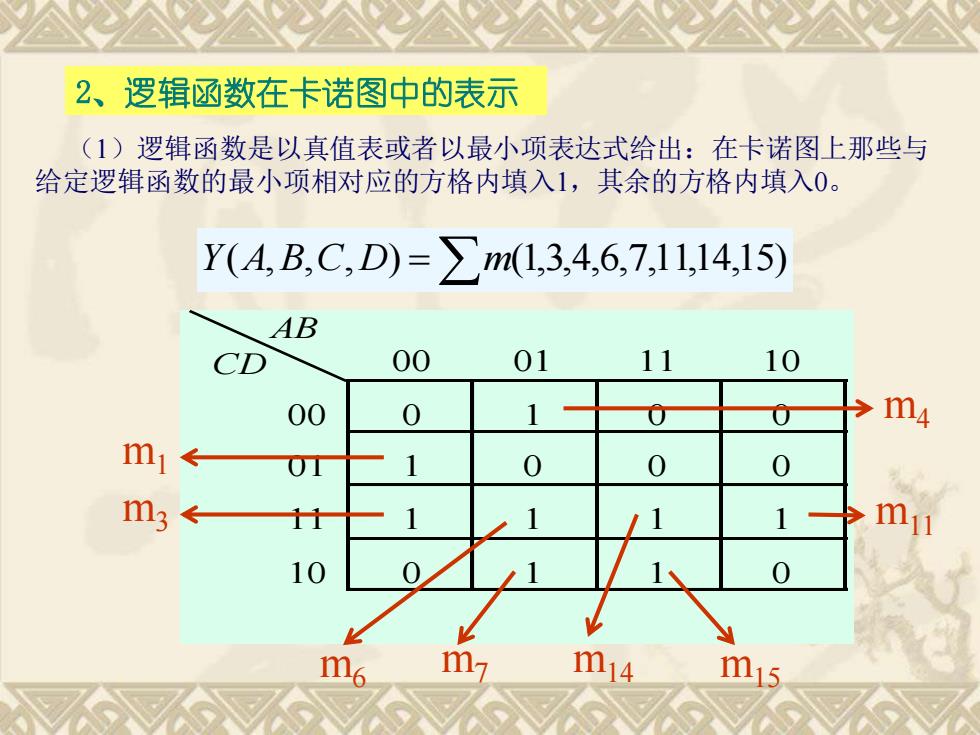
2、逻辑函数在卡诺图中的表示 (1)逻辑函数是以真值表或者以最小项表达式给出:在卡诺图上那些与 给定逻辑函数的最小项相对应的方格内填入1,其余的方格内填入0。 AB CD 00 01 11 10 00 0 1 0 0 01 1 0 0 0 11 1 1 1 1 10 0 1 1 0 Y(A,B,C,D) =m(1,3,4,6,7,11,14,15) m1 m3 m4 m6 m7 m11 m14 m15