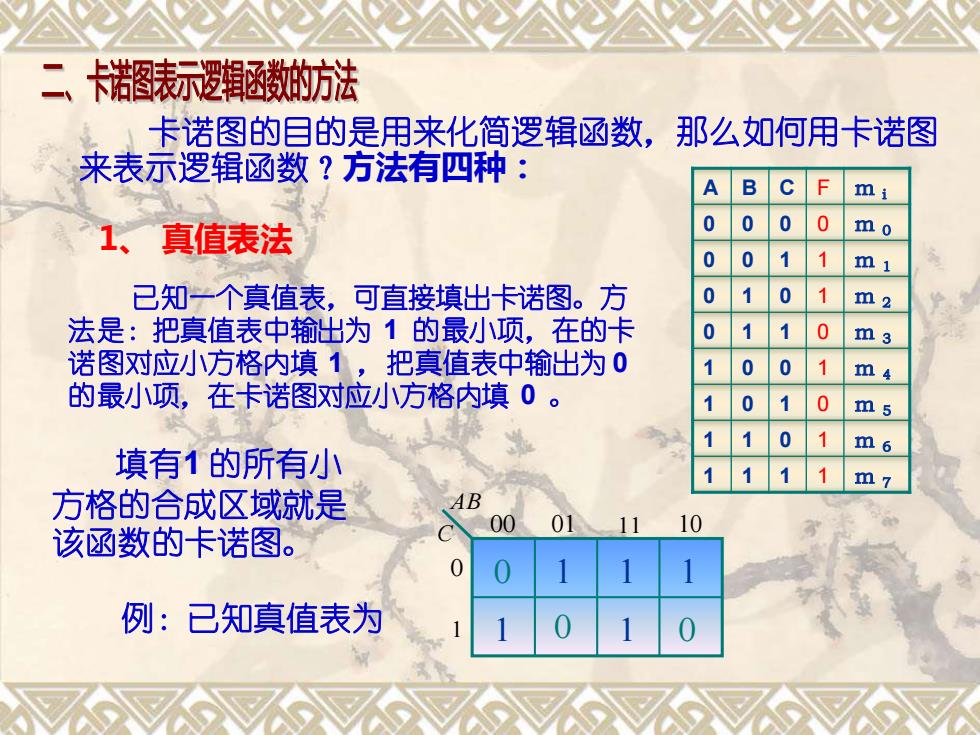
二、卡诺图表示逻辑函数的方法 卡诺图的目的是用来化简逻辑函数,那么如何用卡诺图 来表示逻辑函数?方法有四种: B F m i 1、真值表法 0 mo 1 m1 已知一个真值表,可直接填出卡诺图。方 1 0 m 2 法是:把真值表中输出为1的最小项,在的卡 1 0 m3 诺图对应小方格内填1,把真值表中输出为0 0 m4 的最小项,在卡诺图对应小方格内填0。 0 1m5 0 1 m6 填有1的所有小 m7 方格的合成区域就是 AB 00 01 该函数的卡诺图。 0 例:已知真值表为
AB C 00 01 11 10 1 0 卡诺图的目的是用来化简逻辑函数,那么如何用卡诺图 来表示逻辑函数?方法有四种: 1、 真值表法 已知一个真值表,可直接填出卡诺图。方 法是:把真值表中输出为 1 的最小项,在的卡 诺图对应小方格内填 1 ,把真值表中输出为 0 的最小项,在卡诺图对应小方格内填 0 。 例:已知真值表为 A B C F m i 0 0 0 0 m 0 0 0 1 1 m 1 0 1 0 1 m 2 0 1 1 0 m 3 1 0 0 1 m 4 1 0 1 0 m 5 1 1 0 1 m 6 填有 1 1 1 1 m 7 1 的所有小 方格的合成区域就是 该函数的卡诺图。 0 1 1 0 1 0 1 1

2、配项法 首先通过配项法将非标准与一或式变换为标准与或式。 即最小项之和的形式。 阿例:F=ABC+ABD+AC(四变量函数) =ABC (D+D)+BD C+C)+AC(B+BD+D ABCD+ABCD+ABCD+ABCD+ABCD+ABCD+ABCD+ABCD m13+m12+m+m+m15+m1o+m14+m1 =∑5,7,10~15) AB 00 011110 CD 0 将F中的所有最小项填在 0 0 0 卡诺图的对应小方格内。最小项 01 0 填“1”,其余位置填“0”。 11 0 画出四变量卡诺图,并填图: 100 0
AB CD 00 01 11 10 00011110 例: F = ABC + ABD + AC = ABC (D + D) + ABD (C +C)+ AC(B + B)(D + D) = ABCD+ ABCD+ ABCD + ABCD+ ABCD + ABCD+ ABCD+ ABCD = m13 + m12 + m7 + m5 + m15 + m10 + m14 + m11 = ( ) m 5,7,10 ~15 画出四变量卡诺图,并填图: 将 F 中的所有最小项填在 卡诺图的对应小方格内。最小项 填“1”,其余位置填“0” 。 2、配项法 (四变量函数) 1 1 1 1 1 1 1 1 首先通过配项法将非标准与-或式变换为标准与或式。 即最小项之和的形式。 0 0 0 0 0 0 0 0

3、直接观察法:(填公因子法) AB CD 00 01,1110 例:F=ABC+ABD+AC 00 01 ABC ABC(D+D) 11 =ABCD+ABCD 10 =m13+m12 ABC是m13和m12的公因子 所以只要在A=B=1,C=0所对应的区域填1即可。 同理:在A=0,B=D=1 所对应的区域填1。 在A=1,C=1所对应的区域填1
AB CD 00 01 11 10 00011110 例:F = ABC + ABD + AC ABC = ABC(D + D) = ABCD+ ABCD = m13 + m12 ABC 是 m13 和 m12 的公因子 所以只要在 A=B=1 ,C=0 所对应的区域填1即可。 同理:在 A=0, B=D=1 所对应的区域填1。 在 A=1,C=1 所对应的区域填1。 3、直接观察法:(填公因子法) 1 1 1 1 1 1 1 1

4、将最小项之和形式化简为最大项之积形式: 任何二个逻辑函数不但可以表示成最小项之和的形式, 也可以表示为最天项之积的形式。 最大项和最小项互为反函数。 m,M, M,=m 因此:在卡诺图上最小项用“1”格表示,最大项 用“0”格表示
mi = Mi 最大项和最小项互为反函数。 Mi = mi 因此:在卡诺图上最小项用“1”格表示,最大项 用“0”格表示。 4、 将最小项之和形式化简为最大项之积形式: 任何一个逻辑函数不但可以表示成最小项之和的形式, 也可以表示为最大项之积的形式

例:已知F=ABC+ABC+ABC+ABC+ABC+ABC =∑(0,13,5,6,7) AB 00 01 11 10 要求将F表示为最大项之积的形式。 0 解:F=∑(0,135,6,7) 在三变量卡诺图中填“1”格表示 最小项,其余填 “0”格表示最大项 F=ABC+ABC “0”格表示最小项的非。 F=F=ABC+ABC 本例说明:任何一个 逻辑函数,根据需要可以 =(A+B+Ca+B+C) 用“1”格表示,也可以用 =M2M4=Π2,4) “0”格表示
AB C 00 01 11 10 1 0 本例说明:任何一个 逻辑函数,根据需要可以 用“1”格表示,也可以用 “0”格表示。 例:已知 F = ABC + ABC + ABC + ABC + ABC + ABC = ( ) m 0,1,3,5,6,7 要求将F表示为最大项之积的形式。 = ( ) m 解:F 0,1,3,5,6,7 在三变量卡诺图中填“1”格表示 最小项,其余填 “0”格表示最大项 。 1 0 1 0 1 1 1 1 F = ABC + ABC “0”格表示最小项的非。 F = F = ABC + ABC = (A+ B +C)(A+ B +C) = ( ) M = M2 M4 2,4