
约束条件:(2)从A1,A2,A3运到B的物资数量 之和应等于B的需要量,即 X11+X21+X31=3 X12+X22+X32=8 X13+X23+X33=4 X14+X24+X34=6 (3)在不允许有倒运的条件下,运量必须非 负,即 x≥0(i=1,2,3j=1,2,3,4)
约束条件:(2)从A1 ,A2 ,A3 运到Bj的物资数量 之和应等于Bj的需要量,即 (3)在不允许有倒运的条件下,运量必须非 负,即 11 21 31 12 22 32 13 23 33 14 24 34 3 8 4 6 x x x x x x x x x x x x + + = + + = + + = + + = 0 ( 1,2,3; 1,2,3,4) ij x i j = =
例三]指派问题 某公司经理委派4个推销员到4个地区推销某种 商品。4个推销员各有不同的经验和能力,因 而他们在每个地区获得的利润不同,其评估值 如下表5-3所示: 推销员 地区 2 3 4 35 27 28 37 28 34 29 40 35 24 32 33 24 32 25 28 问公司经理如何分配4个推銷员才能使总利润 最大?
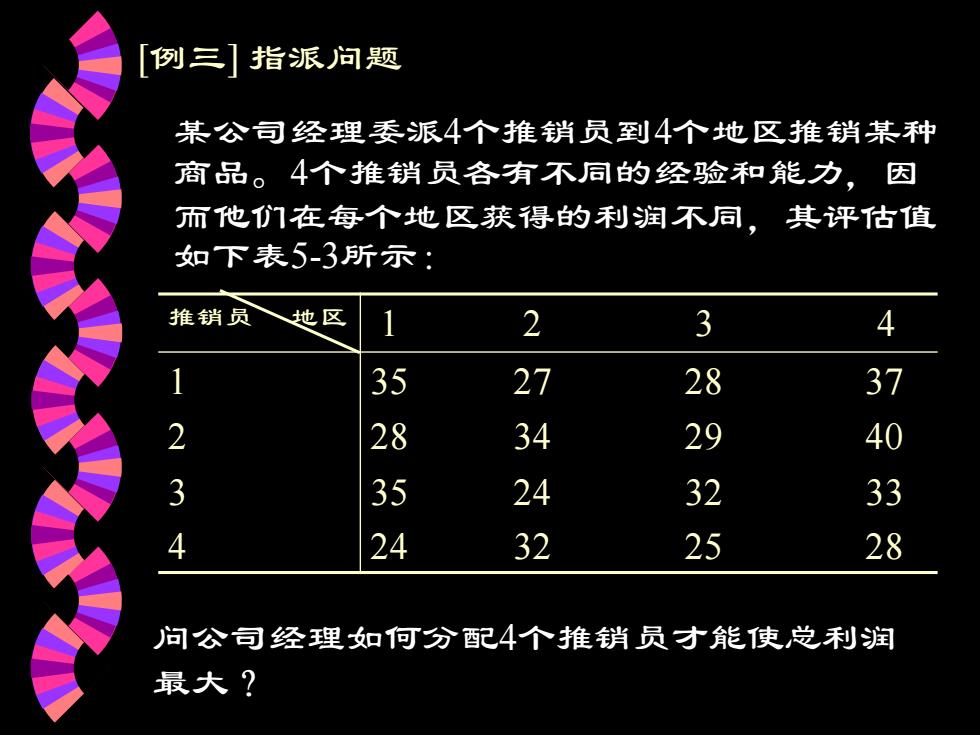
[例三] 指派问题 某公司经理委派4个推销员到4个地区推销某种 商品。4个推销员各有不同的经验和能力,因 而他们在每个地区获得的利润不同,其评估值 如下表5-3所示: 推销员 地区 1 2 3 4 1 2 3 4 35 27 28 37 28 34 29 40 35 24 32 33 24 32 25 28 问公司经理如何分配4个推销员才能使总利润 最大?

设 1 当派第个推销员到第j个地区 0,当不派第个推销员到第j个地区 C表示第个推销员到第j个地区获得 的利润,则数学模型为: 目标函数:maxZ= ∑∑Cx i- 约束条件: 之x,=1j=12,34 x=1,i=1,2,3,4 x=0 或1
设 Cij表示第i个推销员到第j个地区获得 的利润,则数学模型为: 目标函数: 约束条件: 1, 0, ij i x i = 当派第 个推销员到第j个地区 当不派第 个推销员到第j个地区 4 4 1 1 max ij ij i j Z C x = = = 4 1 4 1 1, 1, 2,3, 4 1, 1, 2,3, 4 0 1 ij i ij j ij x j x i x = = = = = = = 或

例四]非线性规划 某公司经营两种设备,第一种设备每件 售价30元,第二种设备每件售价450元, 据统计,售出一件第一种设备所需要的 营业时间平均是0.5小时,第二种设备是 (2+0.25X2)小时,其中X2是第二种设备 的售出数量。已知该公司在这段时间内 总营业时间为800小时,试决定使营业颜 最大的营业计划
[例四]非线性规划 某公司经营两种设备,第一种设备每件 售价30元,第二种设备每件售价450元, 据统计,售出一件第一种设备所需要的 营业时间平均是0.5小时,第二种设备是 (2+0.25x2)小时,其中x2是第二种设备 的售出数量。已知该公司在这段时间内 总营业时间为800小时,试决定使营业额 最大的营业计划

设该公司计划经营第一种设备X件,第 二种设备X,件,则由题意,其营业额为 f=30x1+450x2 再考虑到营业时间的限制,问题的数 学模型为: 目标函数:maxf=30x,+450x2 约束条件: 0.5x1+(2+0.25x2)x2≤800 x1≥0,x2≥0
设该公司计划经营第一种设备x1件,第 二种设备x2件,则由题意,其营业额为 30 450 1 2 f x x = + 再考虑到营业时间的限制,问题的数 学模型为: 目标函数: 约束条件: max 30 450 1 2 f x x = + 1 2 2 1 2 0.5 (2 0.25 ) 800 0, x 0 x x x x + +