
重点内容: 5.1系统优化方法概述 5.2系统优化模型举例 5.3系统评价概述 5.4层次分析法 (AHP
重点内容: 5.1 系统优化方法概述 5.2 系统优化模型举例 5.3系统评价概述 5.4 层次分析法(AHP)

5.2系统优化模型举例 [例一线性规划问题 某工厂在计划期内要安排生产I、Ⅱ两种产品,已 知生产单位产品所需的设备台时及A、B两种原材料 的消耗如下表所示。该工厂每生产一件产品I可获 利2元,每生产一件产品Ⅱ可获利3元, 问应如何安 排计划可使该工厂获利最多? 表5-1 设备和原材料表 产品 n 限量 投 设备 2 8台时 原材料A 0 16kg 原材料B 0 4 12kg
5.2系统优化模型举例 [例一]线性规划问题 某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品,已 知生产单位产品所需的设备台时及A、B两种原材料 的消耗如下表所示。该工厂每生产一件产品Ⅰ可获 利2元,每生产一件产品Ⅱ可获利3元,问应如何安 排计划可使该工厂获利最多? 表5-1 设备和原材料表 产品 投 入 Ⅰ Ⅱ ≤限量 设备 原材料A 原材料B 1 2 4 0 0 4 8台时 16kg 12kg

设X1,X2分别表示在计划内产品I、Ⅱ的 产量,则 目标丞数: max Z=2x +3x2 满足的条件: x1+2x2≤8 4x1≤16 4x2≤12 X1,X2≥0 这就是该计划问题的线性规划模型
设x1 ,x2分别表示在计划内产品Ⅰ、Ⅱ的 产量,则 目标函数: 满足的条件: 这就是该计划问题的线性规划模型。 max 2 3 Z x x = +1 2 1 2 1 2 1 2 2 8 4 16 4 12 , 0 x x x x x x +
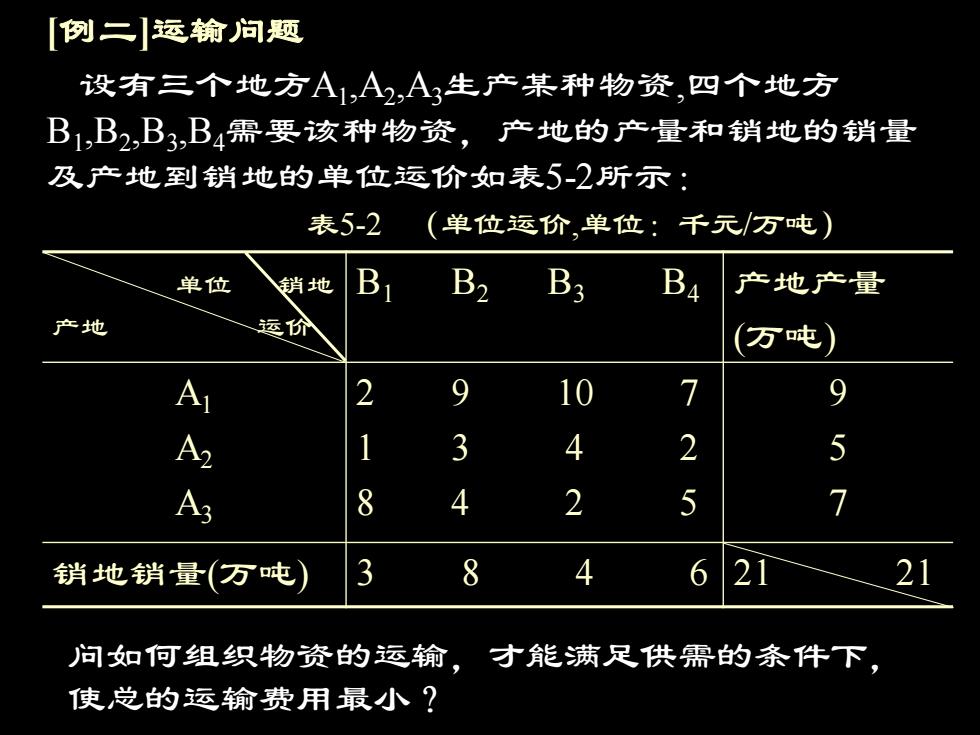
[例二运输问题 设有三个地方A1,A2,A3生产某种物资,四个地方 B1,B2,B3,B4需要该种物资,产地的产量和销地的销量 及产地到销地的单位运价如表5-2所示: 表5-2 (单位运价,单位:千元/万吨) 单位 销地 B2 B3 Ba 产地产量 产地 运价 (万吨) A 10 7 3 4 2 A3 8 4 2 5 销地销量(万吨 8 4 6 问如何组织物资的运输,才能满足供需的条件下 使总的运输费用最小?
单位 销地 产地 运价 B1 B2 B3 B4 产地产量 (万吨) A1 A2 A3 2 9 10 7 1 3 4 2 8 4 2 5 9 5 7 销地销量(万吨) 3 8 4 6 21 21 表5-2 (单位运价,单位:千元/万吨) 问如何组织物资的运输,才能满足供需的条件下, 使总的运输费用最小? [例二]运输问题 设有三个地方A1 ,A2 ,A3生产某种物资,四个地方 B1 ,B2 ,B3 ,B4需要该种物资,产地的产量和销地的销量 及产地到销地的单位运价如表5-2所示:

本问题是一个总产量等于总销量的运输问题, 通常称为“产销平衡问题”。 设A运到B的物资数量为x(=1,2,3;j=1,2,3,4),总 运费为∫,则数学模型为: 目标函数: minf=2x1+9x2+10x3+7x4+x21 +3x22+4x23+2x24+8x31 +4x32+2x33+5X34 约束条件:(1)A运到B1,B2,B3,B4的物资数量之 和应等于A的产量,即 X1+X2+X13+x4=9 X21+X22+23+x24=5 X31+X2+X3+X34=7
本问题是一个总产量等于总销量的运输问题, 通常称为“产销平衡问题”。 设Ai运到Bj的物资数量为xij(i=1,2,3;j=1,2,3,4),总 运费为f,则数学模型为: 目标函数: 约束条件:(1)Ai运到B1 ,B2 ,B3 ,B4的物资数量之 和应等于Ai的产量,即 11 12 13 14 21 22 23 24 31 32 33 34 min 2 9 10 7 3 4 2 8 4 2 5 f x x x x x x x x x x x x = + + + + + + + + + + + 11 12 13 14 21 22 23 24 31 32 33 34 9 5 7 x x x x x x x x x x x x + + + = + + + = + + + =