
(2.6) 相对误差可表达为: 令:成-上,成一5,,,-为各直接测量物理量的相对误差,则: X2 X。 (2.7) 试,袋为格系数。根紧这一原可以得列加下常用故式的相时计京式 (1)和的误差 y=5+6+- (2.8) (2.9) (2)积的误差 y=X·,x (2.10) 6=±∑x (2.11) (3)商的误差 (2.12 6=±0x+成, (2.13) (4)幂的误差 y=x (2.14) 8=±(n+远) (2.15 (5)开方误差 y (2.16) This document is produced by trial version of Print2Flash.Visit www.print2flash.com for more information

6=园 (2.17) 例如在用引伸计测定弹性模量E时,需根据下式计算: E (2.18) △LA 式中:△F为载荷增量:L为引伸仪标距:△L为变形增量的平均值:A为截面面积。如果试件为圆 截面,因A=πd/4,计算E的相对误差为: 0e=0n+d+0a+2δa (2.18) 可见,试件横截面的尺寸测量误差对弹性模量的影响较大,测量中要给以足够重视。通常要 求测量上、中、下三个截面,每个截面测量相互垂直的两个直径,再取平均值 2.5数据表示方法 力学实验的目的是要通过实验手段测定一些力学参数或探索未知的力学规律。这就要求我们 尽可能用简洁清晰的方法表达实验数据,以使我们容易把握输入输出关系,作出正确地分析判断 常用的数据表示方法有表格法、图像法和公式法三种。它们既是三种独立的数据表示方法,有时 又是数据处理的三个不同阶段。 2.5.1表格法 表格法又称列表表示法,分为关系表格和汇总表格两类。 关系表格表达的是相互有关联的数据,即表中行与行、列与列之间的数据有联系。关系表格 既起着记录和保存原始数据的作用,也是图像法和公式法的基础。就其功能而言,可分为原始记 录表和整理数据表。前者是为方便记录原始实验数据设计的表格,包括一些反映测量方法的栏目 如应变仪的通道号与应变片编号的对应等:后者则是为 反映输入输出关系 经过 时原始记录数 据整理之后设计的表格,通常会去掉不合理的数据和反映测量方法的栏目,增加中间计算结果栏 目等。如果表格设计合理,分析方便,也可将两个表格合二为一。 汇总表格主要用于表达实验结果的汇总数据,起若摘要和结论的作用,表中行与行、列与列 之间的数据不一定右联系。 表格的设计没有固定的格式,通常根据观测数据的多少和数据分析需要独立进行设计,但注 意以下几点是重婴的 (1)每个表格要有名称,不同的表格要有编号。 (2)各栏表头要有简洁确切的名称,并注明单位。 (3)栏目的设计应充分反映数据间的联系和计算顶序,力求简明、齐全、有条理。 (4)数值的写法要整齐统一,有效位数的取会合乎相关标准及所用设备精度的要求,小数点 要对齐等。 2.5.2图像法 表格法虽然具有记录和保存原始试验数据的突出优势,对于一些常规试验,可以直接采用表 This document is produced by trial version of Print2Flash.Visit www.print2flash.com for more information
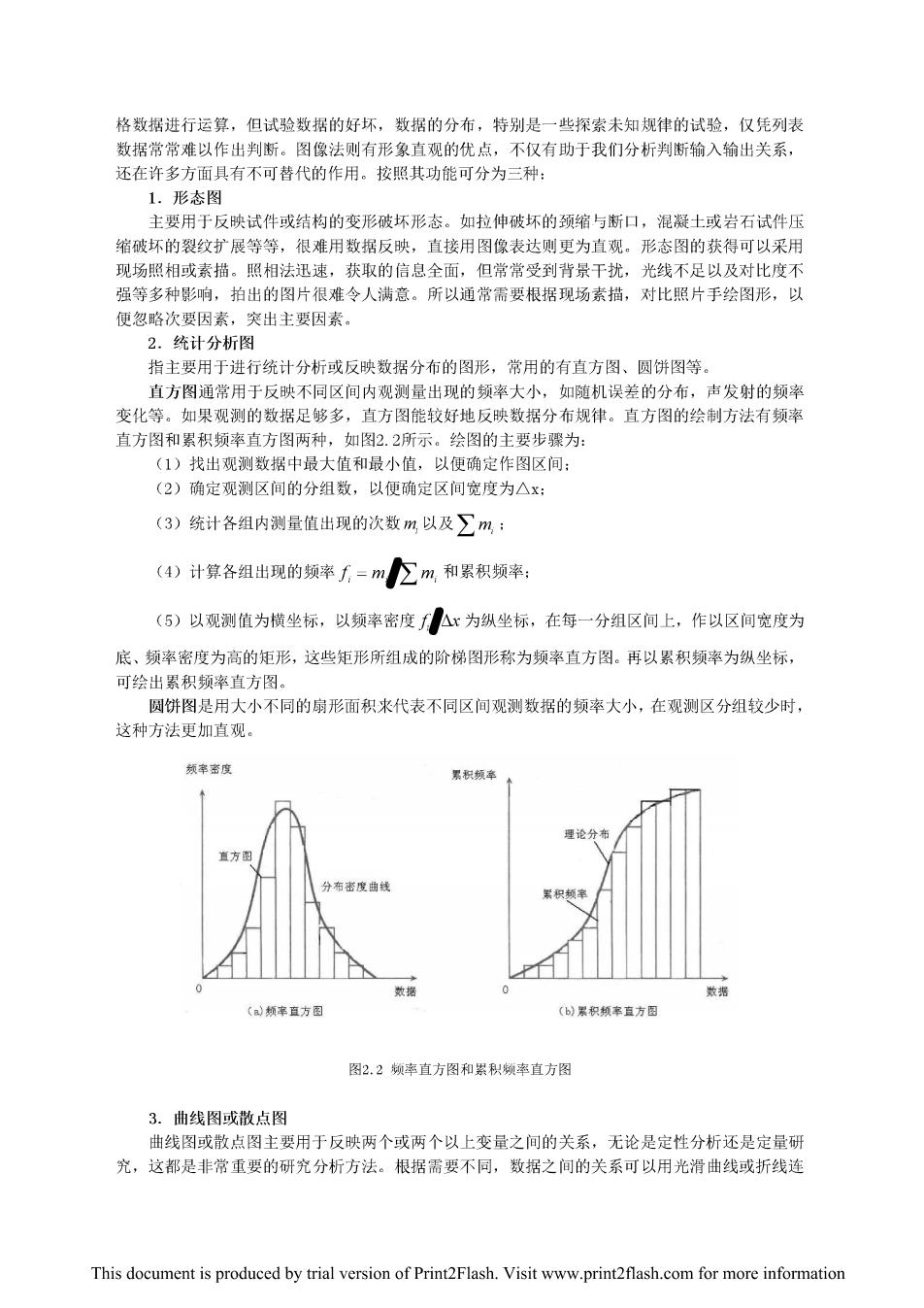
格数据进行运算,但试验数据的好坏,数据的分布,特别是一些探索未知规律的试验,仅凭列表 数据常常难以作出判断。图像法侧有形象直观的优点,不仅有助于我们分析判断输入输出关系。 还在许多方面具有不可替代的作用。按照其功能可分为三种 1.形态图 主要用于反映试件或结构的变形破坏形态。如拉伸破坏的颈缩与断口,混凝土或岩石试件压 缩破坏的裂纹扩展等等,很难用数据反映,直接用图像表达则更为直观,形态图的获得可以采用 现场照相或素描。照相法迅速,获取的信息全面,但常常受到背景干扰,光线不足以及对比度不 强等多种影响,拍出的图片很难令人满意。所以通常需要根据现场素描,对比照片手绘图形,以 便忽略次要因素,突出主要因素。 2.统计分析图 指主要用于进行统计分析或反映数据分布的图形,常用的有直方图、圆饼图等。 直方图通常用于反融不同风间内观调量出现的频率大小,如随机误差的分布,声发射的频率 交化等。如果观测的数据足够多。 直方图能较好地反映数据分布规律。直方图的绘制方法有频率 直方图和累积顷率直方图两种, 如图2.2所示。绘图的主要步骤为: (1)找出观测数据中最大值和最小值,以使确定作图区间: (2)确定观测区间的分组数,以便确定区间宽度为△x: (3)统计各组内测量值出现的次数m以及∑m: (4)计算各组出现的频率=m∑m,和累积领率 (5)以观测值为横坐标,以频率密度f△x为纵坐标,在每一分组区间上,作以区间完度为 底、频率密度为高的矩形,这些矩形所组成的阶梯图形称为频率直方图。再以累积频率为纵坐标, 可绘出累积须率直方图。 圆饼图是用大小不同的扇形面积来代表不同区间观测数据的频率大小,在观测区分组较少时 这种方法更加直观。 累积烦率 (心机率直方图 ()黑积频率直方图 图2.2期率直方图和紫积期率直方图 3.曲线图或散点图 曲线图或散点图主要用于反映两个或两个以上变量之间的关系,无论是定性分析还是定量研 究,这都是非常重要的研究分析方法。根据需要不同,数据之间的关系可以用光滑曲线或折线连 This document is produced by trial version of Print2Flash.Visit www.print2flash.com for more information

接,也可以直接绘成散点图。就应用最多的平面图形而言,绘制中注意以下几点: (1)横坐标取为自变量,竖坐标取为因变量,方向逸取一般采用“右手坐标系” (2)同一坐标系中,自变量和因变量一般只有一个。在不至于造成混滑的情况下,因变量可 以取两个或两个以上,但自变量通常只有 (3)将数据之间的对应关系依次用坐标点表示,即“打点”。“点”是原始试验数据,要标注 醒目。统一坐标中反映不同状态的数据关系时,要采用不同的“打点”符号,如“O”“+”、“口”、 “△”、“X”等等 (4)数据点可以用光滑曲线连接,也可依次直线连接成折线。由于“曲线”未必反映数据之 间的真实关系,折线反而用得更多。折线在这里更多得是 接数据的作用。不同状态的数据 点应采用不同的线型,如实线、虚线、点划线和点线等,以便区别。如果数据点的变化关系清晰, 也可不连线,直接采用散点图。 (5)与试验数据有关的条件参数,可以在图中空白处或图名下方补充注明。 2.5.3公式法 公式法就是用一个或一组函数关系式反映输入输出数据之间的依赖关系。函数关系式由于变 化规律清晰,表达简洁直观,便于运算,使用方便,在探索未知规律的试验中,常常是人们的终 极追求目标。由于这种函数关系由试验结果分析得到,而非理论分析而米,一般称为经验公式。 一个数学建模过程,在数理统计学 ,在很大程度上取决于测量人员的数学功底、经验 和分析判断能力。建立经验公式的主要步骤为: (1)根据整理的数据表,选取合适的坐标,绘出数据折线或散点图。 (2)根据折线或散点图的形状判断可能的函数关系,建立回归方程。值得注意的是坐标选取 巧妙有助于回归方程的建立,如双对数坐标上的直线分布意味着一种幂函数关系等。 (3)试验选取的回归方程,求出待定常数,并进行相关性检验 1.函数关系选择 回归方程一般选用常见的初等函数或这些函数的组合,常见的初等函数有: y=a+bx (2.19) y=ab (2.20) y=ae (2.21) y=ad (2.22) y=a+bx (2.23) 1 y= a+be (2.24) 值得注意的是,对同一组试验数据,回归结果可能不唯一,即不同的分析得到的经验公式可 能不同。公式越简单,参数越少,误差越小的自然就越好。 2.待定常数的求法 This document is produced by trial version of Print2Flash.Visit www.print2flash.com for more information
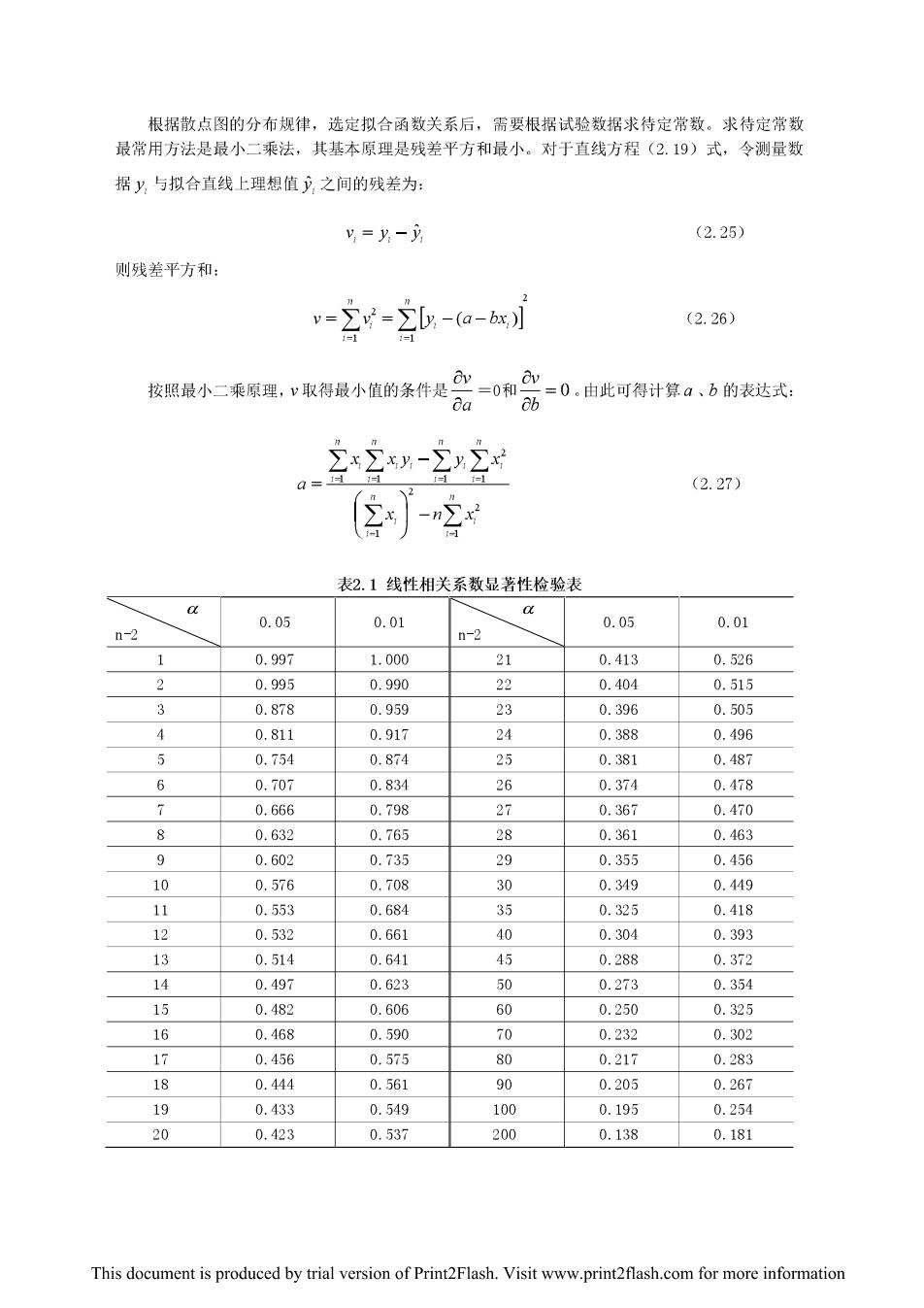
根据散点图的分布规律,选定拟合函数关系后,需要根据试验数据求待定常致。求待定常数 最常用方法是最小二乘法,其基本原理是残差平方和最小。对于直线方程(2.19)式,令测量数 据y与拟合直线上理想值乃之间的残差为 y=片- (2.25) 则残差平方和: v=Zv=Ly-(a-bx) (2.26) 较照最小乘原理,V取得最小值的条件是=0和, =0,由此可得计算a、b的表达式: (2.27) ②2 表2.1线性相关系数显著性检验表 0.05 0.01 n-2 0.05 0.01 n-2 1 0.99 1.000 21 0.413 0.526 2 0.995 0.990 22 0.404 0.515 0.878 0.959 23 0.396 0.505 0.811 0917 24 0288 0496 0.754 0.874 0.381 0.487 0.70 0.831 26 0.374 0.478 0.666 0.798 27 0.367 0.470 0639 0765 0261 0.463 0 0.602 0.735 30 0.355 0.456 10 0.570 0.708 30 0.349 0.449 11 0.553 0.684 35 0.325 0.418 12 0532 0661 40 020M 0.393 0.514 0.641 45 0.288 0.372 14 0.491 0.623 50 0.273 0.354 15 0.482 0.606 60 0.250 0.325 16 0468 0590 =0 0.232 0.302 公 0.456 0.575 0.217 0.283 18 0.44 0.561 90 0.205 0.267 19 0.433 0.549 100 0.195 0.254 20 0.423 0.537 200 0.138 0.181 This document is produced by trial version of Print2Flash.Visit www.print2flash.com for more information