
第10卷第3期 智能系统学报 Vol.10 No.3 2015年6月 CAAI Transactions on Intelligent Systems Jun.2015 D0:10.3969/j.issn.1673-4785.201405070 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.tp.20150611.0902.001.html 广义中心混合蛙跳算法 赵嘉,吕莉,樊棠怀 (南昌工程学院信息工程学院,江西南昌330099) 摘要:为解决标准混合蛙跳算法族群之间信息共享能力差的问题,加强族群内蛙的学习能力,利用各族群最优蛙 位置的平均中心,构造一个与各族群最优蛙都有关联的虚拟广义中心蛙,提出广义中心混合蛙跳算法。该算法在进 化过程中,首先蛙群最优蛙在原有位置及广义中心蛙的位置上进行“贪梦”选择,选择最好位置作为新的族群最优蛙 位置:其次将广义中心蛙的优势运用于蛙跳规则中,在标准混合蛙跳算法的蛙跳规则中加入族群最差蛙向广义中心 蛙学习的能力。将本文算法与不同维度下的标准混合蛙跳算法及新近提出的知名群智能算法进行比较,实验结果 表明,本文算法在解的精度、收敛速度及解的稳定性等方面具有更优的性能。 关键词:蛙跳算法;混合蛙跳算法;广义中心:蛙跳规则:群智能算法 中图分类号:TP301文献标志码:A文章编号:1673-4785(2015)03-0414-08 中文引用格式:赵嘉,吕莉,樊棠怀.广义中心混合蛙跳算法[J].智能系统学报,2015,10(3):414-421. 英文引用格式:ZHAO Jia,LYU Li,FAN Tanghuai..Shuffled frog-leaping algorithm based on the general center[J].CAAI Trans- actions on Intelligent Systems,2015,10(3):414-421. Shuffled frog-leaping algorithm based on the general center ZHAO Jia,LYU Li,FAN Tanghuai (School of Information Engineering,Nanchang Institute of Technology,Nanchang 330099,China) Abstract:In this paper,a shuffled frog-leaping algorithm based on general center (GC-SFLA)is proposed to solve the problem of weak information sharing between memeplexes in the shuffled frog leaping algorithm(SFLA)to en- hance the learning ability and use the average center of optimal frog.The proposed GC-SFLA generates a virtual general center frog from the optimal frog of each memeplex.Firstly,the optimal frog selects the best location among the original location and general center greedily as new location of new memeplex.After that,the advantage of gen- eral center frog is applied to the frog-leaping rule,which enable the worst frog to learn from the general center frog. Experiments are conducted on a set of swarm intelligence algorithms to verify that the new approach outperforms SF- LA in different dimensions.The experiment results present promising performance of the GC-SFLA on convergence velocity,precision and stability of solution. Keywords:frog-leaping algorithm;shuffled frog leaping algorithm (SFLA);general center;frog leaping rule; swarm intelligence algorithms 混合蛙跳算法(shuffled frog leaping algorithm, SLA))是一种基于群体智能的亚启发式协同搜索 计算技术,最早由M.M.Eusuff和K.E.Lansey于 收稿日期:2014-06-03.网络出版日期:2015-06-11. 基金项目:国家自然科学基金资助项目(61261039,61263029):江西 2000年提出。它结合了基于基因进化的模因演算 省自然科学基金资助项目(20132BAB211031):江西省科 法(memetic algorithm,MA)[2)和基于群体行为的粒 技厅科技支撑项目(20142BBC70034):南昌市科技计划项 目(2013HZCG006,2013HZCG011,2014HZZC008). 子群优化算法(particle swarm optimization,PSO)[) 通信作者:赵嘉.E-mail:zhaojia925@163.com
第 10 卷第 3 期 智 能 系 统 学 报 Vol.10 №.3 2015 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2015 DOI:10.3969 / j.issn.1673⁃4785.201405070 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20150611.0902.001.html 广义中心混合蛙跳算法 赵嘉,吕莉,樊棠怀 (南昌工程学院 信息工程学院,江西 南昌 330099) 摘 要:为解决标准混合蛙跳算法族群之间信息共享能力差的问题,加强族群内蛙的学习能力,利用各族群最优蛙 位置的平均中心,构造一个与各族群最优蛙都有关联的虚拟广义中心蛙,提出广义中心混合蛙跳算法。 该算法在进 化过程中,首先蛙群最优蛙在原有位置及广义中心蛙的位置上进行“贪婪”选择,选择最好位置作为新的族群最优蛙 位置;其次将广义中心蛙的优势运用于蛙跳规则中,在标准混合蛙跳算法的蛙跳规则中加入族群最差蛙向广义中心 蛙学习的能力。 将本文算法与不同维度下的标准混合蛙跳算法及新近提出的知名群智能算法进行比较,实验结果 表明,本文算法在解的精度、收敛速度及解的稳定性等方面具有更优的性能。 关键词:蛙跳算法;混合蛙跳算法;广义中心;蛙跳规则;群智能算法 中图分类号:TP301 文献标志码:A 文章编号:1673⁃4785(2015)03⁃0414⁃08 中文引用格式:赵嘉,吕莉,樊棠怀. 广义中心混合蛙跳算法[J]. 智能系统学报, 2015, 10(3): 414⁃421. 英文引用格式:ZHAO Jia, LYU Li, FAN Tanghuai. Shuffled frog⁃leaping algorithm based on the general center[J]. CAAI Trans⁃ actions on Intelligent Systems, 2015, 10(3): 414⁃421. Shuffled frog⁃leaping algorithm based on the general center ZHAO Jia, LYU Li, FAN Tanghuai (School of Information Engineering, Nanchang Institute of Technology, Nanchang 330099, China) Abstract:In this paper, a shuffled frog⁃leaping algorithm based on general center (GC⁃SFLA) is proposed to solve the problem of weak information sharing between memeplexes in the shuffled frog leaping algorithm (SFLA) to en⁃ hance the learning ability and use the average center of optimal frog. The proposed GC⁃SFLA generates a virtual general center frog from the optimal frog of each memeplex. Firstly, the optimal frog selects the best location among the original location and general center greedily as new location of new memeplex. After that, the advantage of gen⁃ eral center frog is applied to the frog⁃leaping rule, which enable the worst frog to learn from the general center frog. Experiments are conducted on a set of swarm intelligence algorithms to verify that the new approach outperforms SF⁃ LA in different dimensions. The experiment results present promising performance of the GC⁃SFLA on convergence velocity, precision and stability of solution. Keywords: frog⁃leaping algorithm; shuffled frog leaping algorithm ( SFLA); general center; frog leaping rule; swarm intelligence algorithms 收稿日期:2014⁃06⁃03. 网络出版日期:2015⁃06⁃11. 基金项目:国家自然科学基金资助项目( 61261039,61263029);江西 省自然科学基金资助项目( 20132BAB211031);江西省科 技厅科技支撑项目(20142BBG70034);南昌市科技计划项 目(2013HZCG006,2013HZCG011,2014HZZC008). 通信作者:赵嘉. E⁃mail: zhaojia925@ 163.com. 混合蛙跳算法( shuffled frog leaping algorithm, SFLA) [1]是一种基于群体智能的亚启发式协同搜索 计算技术,最早由 M. M. Eusuff 和 K. E. Lansey 于 2000 年提出。 它结合了基于基因进化的模因演算 法(memetic algorithm, MA) [2]和基于群体行为的粒 子群优化算法(particle swarm optimization, PSO) [3]

第3期 赵嘉,等:广义中心混合蛙跳算法 415· 的优点[),具有概念简单、参数设置少、计算速度 将蛙群分成m个族群,每个族群包含n只青蛙,满 快、全局寻优能力强、易于实现等特点[),并在无线 足关系F=m×n。族群的划分规则是:第1只青蛙 传感器网络覆盖优化、函数优化)、经济负荷分 进入第1个族群,第2只青蛙进入第2个族群,第m 配)]、生产调度组合优化]等领域取得较好应用, 只青蛙进入第m个族群,第m+1只青蛙又进入第1 正成为智能计算领域的研究热点。 个族群,第m+2只青蛙进人第2个族群,以此类 与其他群智能算法相似,混合蛙跳算法也存在 推,直至所有青蛙划分完毕。第k个族群中最好的 易陷入局部极值、进化后期收敛速度慢、计算精度低 一个青蛙,记为,相应地可以得到一个最差的青 等缺点。为此,研究人员在不断深入研究和分析后, 蛙,记为P。 提出了多种不同思想的改进混合蛙跳算法,比较有 为了获得更多的食物,较差的蛙受较好蛙的影 代表性的有罗雪晖等[o]在混合蛙跳算法中加入调 响而跳向较好的蛙。根据上述初始蛙跳规则,第 整序思想设计了局部搜索策略,并在全局信息交换 个青蛙族群中最差蛙的更新公式为: 中加入变异算法,提出一种改进的混合蛙跳算法并 D=r×(Ph-P) (1)》 应用于求解TSP问题:T.Niknam等[]利用混沌局 Pr.=P+Dk,-Das≤D:≤Dx(2) 部搜索策略提出改进的混沌混合蛙跳算法;借鉴分 式中:k表示是第几个族群,且1≤k≤m;r为[0, 子动力学模拟的思想,张潇丹[]提出基于分子动力 1]的随机数:D,为第k个族群最差蛙移动的步长: 学模拟的改进混合蛙跳算法:Sun等[)提出一种基 P"-"为第k个族群最差蛙更新后新位置;D为蛙 于粒子共享的粒子群蛙跳混合优化算法,算法利用 的最大跳动步长。 粒子群具有良好全局搜索性能与混合蛙跳算法具有 若执行更新策略(1)和(2)后,P"对应的适 较强局部搜索能力的特点,克服了群体智能算法后 应值优于P对应的适应值,则用P"取代P;否 期易陷入局部最优及“早熟”收敛的缺点。这些算 则采用P。代替式(1)中的P,重新更新P。若 法都在标准SLA基础上进行不同程度的改进,但 重新执行更新后,P"对应的适应值优于P对应 其改进也不同程度增加了算法的复杂性。 的适应值,则用P"取代P;否则采用式(3)随机 在SFLA中,青蛙的跳跃主要经历局部搜索和 产生一个新的蛙代替P。 全局信息交换2个阶段,局部搜索使模因信息在局 Pg=r×(0ns-0in)+0nma (3) 部个体间进行传递,全局信息交换使得局部间的模 式中:O和0m分别表示算法搜索范围的最大值 因信息得到交换,这在很大程度上决定了算法的收 和最小值。 敛速度与解的质量。但青蛙在进化过程中,族群中 重复以上的更新操作,直至满足事先设定的族 的最差青蛙只向自身蛙群和最优青蛙所在蛙群的最 群内的算法迭代次数。当所有族群的局部深度搜索 好青蛙学习,族群之间的相互学习不够、共享能力不 完成以后,进行全局信息交换。局部深度搜索和全 强。为此,利用各族群最优蛙的优势,构造广义中心 局信息交换两阶段交替进行,直到满足相应的结束 青蛙,并改进蛙群的进化策略,使蛙群在原有学习策 条件。 略的基础上,增加向广义中心青蛙学习的能力,提出 广义中心混合蛙跳算法(shuffled frog leaping algo- 2广义中心混合蛙跳算法 rithm based on genernal center,GC-SFLA)。通过对 2.1广义中心策略 8个标准测试函数的实验仿真,将提出的广义中心 在群智能算法中,随着进化的进行,全局极值将 混合蛙跳算法与标准混合蛙跳算法及新近提出的知 会越来越接近最优解。搜索结束后,全局极值将位 名群智能算法比较算法收敛速度和全局寻优能力。 于最优解的邻近区域。与此同时,由于群智能算法 1 混合蛙跳算法 的随机性,每个个体也分布在全局极值的邻近区域。 为了改善全局极值,使其更快向最优解靠近[,iu 混合蛙跳算法是一种基于群体智能的生物进化 等]引入中心粒子。中心粒子由群体的中心位置 算法。该算法模拟湿地中一群青蛙按族群划分的思 形成,伴随于整个搜索过程,除不具有速度外,该粒 想进行觅食。在算法执行时,首先产生F只青蛙组 子具有与其他普通粒子相同的所有性质。其产生的 成蛙群,对于N维优化问题,群体中第i只青蛙表示 方式如式(4)所示: 为X,=(x,x,,x),将蛙群内的青蛙个体按照 适应值进行降序排列,找到全局最好青蛙(解)P。。 x (4) i=1
的优点[4] ,具有概念简单、参数设置少、计算速度 快、全局寻优能力强、易于实现等特点[5] ,并在无线 传感器网络覆盖优化[6] 、函数优化[7] 、经济负荷分 配[8] 、生产调度组合优化[9] 等领域取得较好应用, 正成为智能计算领域的研究热点。 与其他群智能算法相似,混合蛙跳算法也存在 易陷入局部极值、进化后期收敛速度慢、计算精度低 等缺点。 为此,研究人员在不断深入研究和分析后, 提出了多种不同思想的改进混合蛙跳算法,比较有 代表性的有罗雪晖等[10] 在混合蛙跳算法中加入调 整序思想设计了局部搜索策略,并在全局信息交换 中加入变异算法,提出一种改进的混合蛙跳算法并 应用于求解 TSP 问题;T. Niknam 等[11] 利用混沌局 部搜索策略提出改进的混沌混合蛙跳算法;借鉴分 子动力学模拟的思想,张潇丹[12] 提出基于分子动力 学模拟的改进混合蛙跳算法;Sun 等[13] 提出一种基 于粒子共享的粒子群蛙跳混合优化算法,算法利用 粒子群具有良好全局搜索性能与混合蛙跳算法具有 较强局部搜索能力的特点,克服了群体智能算法后 期易陷入局部最优及“早熟”收敛的缺点。 这些算 法都在标准 SFLA 基础上进行不同程度的改进,但 其改进也不同程度增加了算法的复杂性。 在 SFLA 中,青蛙的跳跃主要经历局部搜索和 全局信息交换 2 个阶段,局部搜索使模因信息在局 部个体间进行传递,全局信息交换使得局部间的模 因信息得到交换,这在很大程度上决定了算法的收 敛速度与解的质量。 但青蛙在进化过程中,族群中 的最差青蛙只向自身蛙群和最优青蛙所在蛙群的最 好青蛙学习,族群之间的相互学习不够、共享能力不 强。 为此,利用各族群最优蛙的优势,构造广义中心 青蛙,并改进蛙群的进化策略,使蛙群在原有学习策 略的基础上,增加向广义中心青蛙学习的能力,提出 广义中心混合蛙跳算法( shuffled frog leaping algo⁃ rithm based on genernal center, GC⁃SFLA)。 通过对 8 个标准测试函数的实验仿真,将提出的广义中心 混合蛙跳算法与标准混合蛙跳算法及新近提出的知 名群智能算法比较算法收敛速度和全局寻优能力。 1 混合蛙跳算法 混合蛙跳算法是一种基于群体智能的生物进化 算法。 该算法模拟湿地中一群青蛙按族群划分的思 想进行觅食。 在算法执行时,首先产生 F 只青蛙组 成蛙群,对于 N 维优化问题,群体中第 i 只青蛙表示 为 Xi = (x 1 i ,x 2 i ,...,x N i ) ,将蛙群内的青蛙个体按照 适应值进行降序排列,找到全局最好青蛙(解) Pg 。 将蛙群分成 m 个族群,每个族群包含 n 只青蛙,满 足关系 F = m × n 。 族群的划分规则是:第 1 只青蛙 进入第 1 个族群,第 2 只青蛙进入第 2 个族群,第 m 只青蛙进入第 m 个族群,第 m + 1 只青蛙又进入第 1 个族群,第 m + 2 只青蛙进入第 2 个族群,以此类 推,直至所有青蛙划分完毕。 第 k 个族群中最好的 一个青蛙,记为 P b k ,相应地可以得到一个最差的青 蛙,记为 P w k 。 为了获得更多的食物,较差的蛙受较好蛙的影 响而跳向较好的蛙。 根据上述初始蛙跳规则,第 k 个青蛙族群中最差蛙的更新公式为: Dk = r × (P b k - P w k ) (1) P new_w k = P w k + Dk, - Dmax ≤ Di ≤ Dmax (2) 式中: k 表示是第几个族群,且 1 ≤ k ≤ m ; r 为[0, 1]的随机数; Dk 为第 k 个族群最差蛙移动的步长; P new_w k 为第 k 个族群最差蛙更新后新位置; Dmax 为蛙 的最大跳动步长。 若执行更新策略(1)和(2)后, P new_w k 对应的适 应值优于 P w k 对应的适应值,则用 P new_w k 取代 P w k ;否 则采用 Pg 代替式(1)中的 P b k ,重新更新 P new_w k 。 若 重新执行更新后, P new_w k 对应的适应值优于 P w k 对应 的适应值,则用 P new_w k 取代 P w k ;否则采用式(3)随机 产生一个新的蛙代替 P w k 。 P w k = r × (Omax - Omin ) + Omin (3) 式中: Omax 和 Omin 分别表示算法搜索范围的最大值 和最小值。 重复以上的更新操作,直至满足事先设定的族 群内的算法迭代次数。 当所有族群的局部深度搜索 完成以后,进行全局信息交换。 局部深度搜索和全 局信息交换两阶段交替进行,直到满足相应的结束 条件。 2 广义中心混合蛙跳算法 2.1 广义中心策略 在群智能算法中,随着进化的进行,全局极值将 会越来越接近最优解。 搜索结束后,全局极值将位 于最优解的邻近区域。 与此同时,由于群智能算法 的随机性,每个个体也分布在全局极值的邻近区域。 为了改善全局极值,使其更快向最优解靠近[14] ,Liu 等[15]引入中心粒子。 中心粒子由群体的中心位置 形成,伴随于整个搜索过程,除不具有速度外,该粒 子具有与其他普通粒子相同的所有性质。 其产生的 方式如式(4)所示: x sc d = ∑ F i = 1 x d i (4) 第 3 期 赵嘉,等:广义中心混合蛙跳算法 ·415·

·416: 智能系统学报 第10卷 式中,F为个体总数,d(1≤d≤N)为个体维数,N 次数的增加,各族群的性能将趋同,多样性降低。 为个体总维数,x为第i个体第d维位置。 本文提出一种新的蛙跳规则,该策略借助广义 汤可宗等6通过实验进一步发现,在粒子群优 中心青蛙的特性,使族群内最差粒子在进化过程中, 化算法中,所有个体极值形成的中心相比群体的中 能够学习其他族群内最优粒子。首先,此蛙跳规则 心更能趋近于最优解。为此,将Liu等s提出的中 会增加最差粒子向全局最优点运动的可能:其次,根 心定义为狭义中心(special center,SC),见式(4); 据蛙跳规则的数学表述可知,该操作扩大了最差粒 将个体极值形成的中心定义为广义中心(general 子的搜索范围:再次,各族群在进化过程中形成了自 center,GC),并提出双中心粒子群优化算法。广义 己族群特色,也保证各族群的多样性。其位置更新 中心粒子产生的方式如式(5): 公式与式(2)一致,最差蛙的移动步长更新公式为 =∑pi D4=T1×(Ph-P)+T2×(P则-P)(9) (5) i=1 式中:j∈1,2,…,m,r1、r2为[0,1]的随机数。 式中:p为第i个体第d维极值位置。 若执行更新策略(9)和(2)后,P"对应的适 混合蛙跳算法的基本原理是每只青蛙在族群内 应值优于P,则用P"取代P,否则,最差蛙的 最优青蛙和全群最优青蛙的引导下,“积极”向着最 移动步长更新公式为 优解靠近,青蛙会被吸引到全群最优蛙和族群最优 D=11×(P.-P)+r2×(P-P)(10) 蛙的邻域。混合蛙跳算法的核心思想是族群划分, 若执行更新策略(10)和(2)后,P"对应的适 每个族群均有族群内最优粒子。搜索结束后,每个 应值优于P,则用P"取代P,否则采用式(3) 族群的最优蛙位置位于最优解或其邻近区域,相比 随机生成1个新的个体位置代替原来的P:。 全群最优蛙,族群最优蛙的中心或许会更接近最优 2.3算法流程 解,这一启示给改善混合蛙跳算法提供了思路,为加 GC-SFLA算法的流程如图1所示。 速算法的收敛速度提供了非常有用的信息。借鉴文 献[16]广义中心思想,但混合蛙跳算法中无个体极 开始 值概念。为此,混合蛙跳算法中的广义中心青蛙定 种群初始化 义如下。 定义1广义中心青蛙(general center frog, 种群分割 GCF)在混合蛙跳算法的进化过程中,各族群的 广义中心蛙产生 最优蛙位置表示为P,其中k表示是第几个族群。 并依式(8)更新P。 则广义中心青蛙P则定义为 p=(p) (6) 族群1 族群2 族群 m k= 进化 进化 化 p时可能会跳出边界[Om,Om]成为非可行解,此 时,按照式(7)进行重置。 种群混合 (pee =O, P对>Om pof =0 pre <O (7) 是否游足 N 终止茶 对形成的广义中心青蛙,评估其适应值,从P Y 和P选择较优的解作为新的P。,其公式描述为 结束 (pr,f(P)<f(P) P= (8) 图1GC-SFLA算法流程 (P.,fPa)≤fP) Fig.1 Flowchart of GC-SFLA 式中:f(·)为适应值函数。 2.2蛙跳规则的改进 1)GC-SFLA算法参数设置,包括族群数、族群 标准SFLA算法蛙跳规则过于简单,族群最差 内更新次数L、族群内青蛙数、,混合迭代次数G 蛙向本族群最优蛙学习,最差蛙的可能新位置被限 等的设置。 定在当前蛙与最好蛙位置的线段上6,限制了模因 2)蛙群初始化。初始化蛙群中青蛙位置并评 进化的搜索区域,且青蛙的学习能力不强,随着迭代 估其适应值,记录蛙群最优蛙为P
式中, F 为个体总数, d(1 ≤ d ≤ N) 为个体维数, N 为个体总维数, x d i 为第 i 个体第 d 维位置。 汤可宗等[16]通过实验进一步发现,在粒子群优 化算法中,所有个体极值形成的中心相比群体的中 心更能趋近于最优解。 为此,将 Liu 等[15] 提出的中 心定义为狭义中心( special center, SC),见式(4); 将个体极值形成的中心定义为广义中心( general center, GC),并提出双中心粒子群优化算法。 广义 中心粒子产生的方式如式(5): x gc d = ∑ F i = 1 p d i,best (5) 式中: p d i,best 为第 i 个体第 d 维极值位置。 混合蛙跳算法的基本原理是每只青蛙在族群内 最优青蛙和全群最优青蛙的引导下,“积极”向着最 优解靠近,青蛙会被吸引到全群最优蛙和族群最优 蛙的邻域。 混合蛙跳算法的核心思想是族群划分, 每个族群均有族群内最优粒子。 搜索结束后,每个 族群的最优蛙位置位于最优解或其邻近区域,相比 全群最优蛙,族群最优蛙的中心或许会更接近最优 解,这一启示给改善混合蛙跳算法提供了思路,为加 速算法的收敛速度提供了非常有用的信息。 借鉴文 献[16]广义中心思想,但混合蛙跳算法中无个体极 值概念。 为此,混合蛙跳算法中的广义中心青蛙定 义如下。 定义 1 广义中心青蛙 ( general center frog, GCF) 在混合蛙跳算法的进化过程中,各族群的 最优蛙位置表示为 P b k ,其中 k 表示是第几个族群。 则广义中心青蛙 P gcf 定义为 P gcf = 1 m (∑ m k = 1 P b k) (6) P gcf 可能会跳出边界 [Omin ,Omax] 成为非可行解,此 时,按照式(7)进行重置。 P gcf = Omax, P gcf > Omax P gcf = Omin , P gcf < Omin { (7) 对形成的广义中心青蛙,评估其适应值,从 Pg 和 P gcf 选择较优的解作为新的 Pg ,其公式描述为 Pg = P gcf , f(P gcf ) < f(Pg ) Pg , f(Pg ) ≤ f(P gcf { ) (8) 式中: f(·) 为适应值函数。 2.2 蛙跳规则的改进 标准 SFLA 算法蛙跳规则过于简单,族群最差 蛙向本族群最优蛙学习,最差蛙的可能新位置被限 定在当前蛙与最好蛙位置的线段上[6] ,限制了模因 进化的搜索区域,且青蛙的学习能力不强,随着迭代 次数的增加,各族群的性能将趋同,多样性降低。 本文提出一种新的蛙跳规则,该策略借助广义 中心青蛙的特性,使族群内最差粒子在进化过程中, 能够学习其他族群内最优粒子。 首先,此蛙跳规则 会增加最差粒子向全局最优点运动的可能;其次,根 据蛙跳规则的数学表述可知,该操作扩大了最差粒 子的搜索范围;再次,各族群在进化过程中形成了自 己族群特色,也保证各族群的多样性。 其位置更新 公式与式(2)一致,最差蛙的移动步长更新公式为 Dk = r1 × (P b k - P w k ) + r2 × (P gcf - P w k ) (9) 式中: j ∈ 1,2,...,m , r1 、 r2 为[0,1]的随机数。 若执行更新策略(9)和(2)后, P new_w k 对应的适 应值优于 P w k ,则用 P new_w k 取代 P w k ,否则,最差蛙的 移动步长更新公式为 Dk = r1 × (Pg - P w k ) + r2 × (P gcf - P w k ) (10) 若执行更新策略(10)和(2)后, P new_w k 对应的适 应值优于 P w k ,则用 P new_w k 取代 P w k , 否则采用式(3) 随机生成 1 个新的个体位置代替原来的 P w k 。 2.3 算法流程 GC⁃SFLA 算法的流程如图 1 所示。 图 1 GC⁃SFLA 算法流程 Fig. 1 Flowchart of GC⁃SFLA 1)GC⁃SFLA 算法参数设置,包括族群数、族群 内更新次数 Lmax 、族群内青蛙数、混合迭代次数 Gmax 等的设置。 2)蛙群初始化。 初始化蛙群中青蛙位置并评 估其适应值,记录蛙群最优蛙为 Pg 。 ·416· 智 能 系 统 学 报 第 10 卷
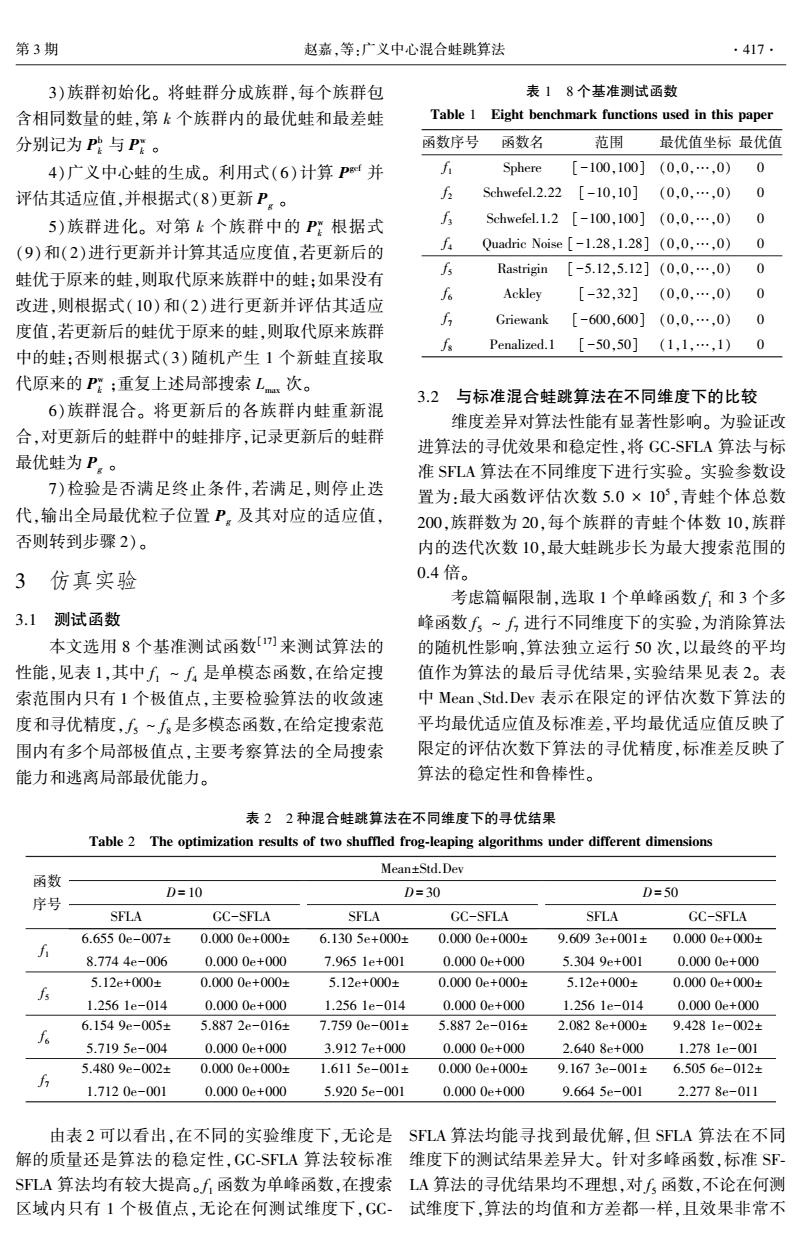
第3期 赵嘉,等:广义中心混合蛙跳算法 ·417- 3)族群初始化。将蛙群分成族群,每个族群包 表18个基准测试函数 含相同数量的蛙,第k个族群内的最优蛙和最差蛙 Table 1 Eight benchmark functions used in this paper 分别记为P与Pg。 函数序号 函数名 范围 最优值坐标最优值 4)广义中心蛙的生成。利用式(6)计算P时并 Sphere [-100.100](0.0.…,0) 0 评估其适应值,并根据式(8)更新P。。 1 Schwefel.2.22 [-10,10] (0,0,…,0) 0 5)族群进化。对第k个族群中的P:根据式 f Schwefel.1.2[-100,100](0,0,…,0) 0 (9)和(2)进行更新并计算其适应度值,若更新后的 Quadric Noise[-1.28,1.28](0,0,…,0) 0 5 Rastrigin [-5.12,5.12](0,0,…,0) 蛙优于原来的蛙,则取代原来族群中的蛙:如果没有 0 Ackley [-32,32](0,0,…,0) 0 改进,则根据式(10)和(2)进行更新并评估其适应 Griewank [-600,600](0,0,…,0) 0 度值,若更新后的蛙优于原来的蛙,则取代原来族群 Penalized..1[-50,50](1,l,…,1)0 中的蛙:否则根据式(3)随机产生1个新蛙直接取 代原来的P:重复上述局部搜索L次。 3.2与标准混合蛙跳算法在不同维度下的比较 6)族群混合。将更新后的各族群内蛙重新混 维度差异对算法性能有显著性影响。为验证改 合,对更新后的蛙群中的蛙排序,记录更新后的蛙群 进算法的寻优效果和稳定性,将GC-SFLA算法与标 最优蛙为P。。 准SFLA算法在不同维度下进行实验。实验参数设 7)检验是否满足终止条件,若满足,则停止迭 置为:最大函数评估次数5.0×10,青蛙个体总数 代,输出全局最优粒子位置P。及其对应的适应值, 200,族群数为20,每个族群的青蛙个体数10,族群 否则转到步骤2)。 内的迭代次数10,最大蛙跳步长为最大搜索范围的 3 仿真实验 0.4倍。 考虑篇幅限制,选取1个单峰函数∫和3个多 3.1测试函数 峰函数∫~,进行不同维度下的实验,为消除算法 本文选用8个基准测试函数[)来测试算法的 的随机性影响,算法独立运行50次,以最终的平均 性能,见表1,其中f~f是单模态函数,在给定搜 值作为算法的最后寻优结果,实验结果见表2。表 索范围内只有1个极值点,主要检验算法的收敛速 中Mean、Std.Dev表示在限定的评估次数下算法的 度和寻优精度,了~∫是多模态函数,在给定搜索范 平均最优适应值及标准差,平均最优适应值反映了 围内有多个局部极值点,主要考察算法的全局搜索 限定的评估次数下算法的寻优精度,标准差反映了 能力和逃离局部最优能力。 算法的稳定性和鲁棒性。 表22种混合蛙跳算法在不同维度下的寻优结果 Table 2 The optimization results of two shuffled frog-leaping algorithms under different dimensions Mean±Std.Dev 函数 D=10 D=30 D=50 序号 SFLA GC-SFLA SFLA GC-SFLA SFLA GC-SFLA 6.6550e-007± 0.0000e+000± 6.1305e+000± 0.0000e+000± 9.6093e+001±0.0000e+000± f月 8.7744e-006 0.0000e+000 7.9651e+001 0.0000e+000 5.3049e+001 0.0000e+000 5.12e+000± 0.0000e+000± 5.12e+000± 0.0000e+000± 5.12e+000± 0.0000e+000± 1.2561e-014 0.0000e+000 1.2561e-014 0.0000e+000 1.2561e-014 0.0000e+000 6.1549e-005± 5.8872e-016± 7.7590e-001± 5.8872e-016± 2.0828e+000± 9.4281e-002± 5.7195e-004 0.0000e+000 3.9127e+000 0.0000e+000 2.6408e+000 1.2781e-001 5.4809e-002± 0.0000e+000± 1.6115e-001± 0.0000e+000± 9.1673e-001± 6.5056e-012± f 1.7120e-001 0.0000e+000 5.9205e-001 0.0000e+000 9.6645e-001 2.2778e-011 由表2可以看出,在不同的实验维度下,无论是SLA算法均能寻找到最优解,但SLA算法在不同 解的质量还是算法的稳定性,GC-SLA算法较标准维度下的测试结果差异大。针对多峰函数,标准SF SFLA算法均有较大提高。f1函数为单峰函数,在搜索LA算法的寻优结果均不理想,对f5函数,不论在何测 区域内只有1个极值点,无论在何测试维度下,GC-试维度下,算法的均值和方差都一样,且效果非常不
3)族群初始化。 将蛙群分成族群,每个族群包 含相同数量的蛙,第 k 个族群内的最优蛙和最差蛙 分别记为 P b k 与 P w k 。 4)广义中心蛙的生成。 利用式(6)计算 P gcf 并 评估其适应值,并根据式(8)更新 Pg 。 5)族群进化。 对第 k 个族群中的 P w k 根据式 (9)和(2)进行更新并计算其适应度值,若更新后的 蛙优于原来的蛙,则取代原来族群中的蛙;如果没有 改进,则根据式(10)和(2)进行更新并评估其适应 度值,若更新后的蛙优于原来的蛙,则取代原来族群 中的蛙;否则根据式(3)随机产生 1 个新蛙直接取 代原来的 P w k ;重复上述局部搜索 Lmax 次。 6)族群混合。 将更新后的各族群内蛙重新混 合,对更新后的蛙群中的蛙排序,记录更新后的蛙群 最优蛙为 Pg 。 7)检验是否满足终止条件,若满足,则停止迭 代,输出全局最优粒子位置 Pg 及其对应的适应值, 否则转到步骤 2)。 3 仿真实验 3.1 测试函数 本文选用 8 个基准测试函数[17] 来测试算法的 性能,见表 1,其中 f 1 ~ f 4 是单模态函数,在给定搜 索范围内只有 1 个极值点,主要检验算法的收敛速 度和寻优精度, f 5 ~ f 8 是多模态函数,在给定搜索范 围内有多个局部极值点,主要考察算法的全局搜索 能力和逃离局部最优能力。 表 1 8 个基准测试函数 Table 1 Eight benchmark functions used in this paper 函数序号 函数名 范围 最优值坐标 最优值 f 1 Sphere [-100,100] (0,0,…,0) 0 f 2 Schwefel.2.22 [-10,10] (0,0,…,0) 0 f 3 Schwefel.1.2 [-100,100] (0,0,…,0) 0 f 4 Quadric Noise [-1.28,1.28] (0,0,…,0) 0 f 5 Rastrigin [-5.12,5.12] (0,0,…,0) 0 f 6 Ackley [-32,32] (0,0,…,0) 0 f 7 Griewank [-600,600] (0,0,…,0) 0 f 8 Penalized.1 [-50,50] (1,1,…,1) 0 3.2 与标准混合蛙跳算法在不同维度下的比较 维度差异对算法性能有显著性影响。 为验证改 进算法的寻优效果和稳定性,将 GC⁃SFLA 算法与标 准 SFLA 算法在不同维度下进行实验。 实验参数设 置为:最大函数评估次数 5.0 × 10 5 ,青蛙个体总数 200,族群数为 20,每个族群的青蛙个体数 10,族群 内的迭代次数 10,最大蛙跳步长为最大搜索范围的 0.4 倍。 考虑篇幅限制,选取 1 个单峰函数 f 1 和 3 个多 峰函数 f 5 ~ f 7 进行不同维度下的实验,为消除算法 的随机性影响,算法独立运行 50 次,以最终的平均 值作为算法的最后寻优结果,实验结果见表 2。 表 中 Mean、Std.Dev 表示在限定的评估次数下算法的 平均最优适应值及标准差,平均最优适应值反映了 限定的评估次数下算法的寻优精度,标准差反映了 算法的稳定性和鲁棒性。 表 2 2 种混合蛙跳算法在不同维度下的寻优结果 Table 2 The optimization results of two shuffled frog⁃leaping algorithms under different dimensions 函数 序号 Mean±Std.Dev D= 10 SFLA GC-SFLA D= 30 SFLA GC-SFLA D= 50 SFLA GC-SFLA f 1 6.655 0e-007± 8.774 4e-006 0.000 0e+000± 0.000 0e+000 6.130 5e+000± 7.965 1e+001 0.000 0e+000± 0.000 0e+000 9.609 3e+001± 5.304 9e+001 0.000 0e+000± 0.000 0e+000 f 5 5.12e+000± 1.256 1e-014 0.000 0e+000± 0.000 0e+000 5.12e+000± 1.256 1e-014 0.000 0e+000± 0.000 0e+000 5.12e+000± 1.256 1e-014 0.000 0e+000± 0.000 0e+000 f 6 6.154 9e-005± 5.719 5e-004 5.887 2e-016± 0.000 0e+000 7.759 0e-001± 3.912 7e+000 5.887 2e-016± 0.000 0e+000 2.082 8e+000± 2.640 8e+000 9.428 1e-002± 1.278 1e-001 f 7 5.480 9e-002± 1.712 0e-001 0.000 0e+000± 0.000 0e+000 1.611 5e-001± 5.920 5e-001 0.000 0e+000± 0.000 0e+000 9.167 3e-001± 9.664 5e-001 6.505 6e-012± 2.277 8e-011 由表 2 可以看出,在不同的实验维度下,无论是 解的质量还是算法的稳定性,GC⁃SFLA 算法较标准 SFLA 算法均有较大提高。 f 1 函数为单峰函数,在搜索 区域内只有 1 个极值点,无论在何测试维度下,GC⁃ SFLA 算法均能寻找到最优解,但 SFLA 算法在不同 维度下的测试结果差异大。 针对多峰函数,标准 SF⁃ LA 算法的寻优结果均不理想,对 f 5 函数,不论在何测 试维度下,算法的均值和方差都一样,且效果非常不 第 3 期 赵嘉,等:广义中心混合蛙跳算法 ·417·
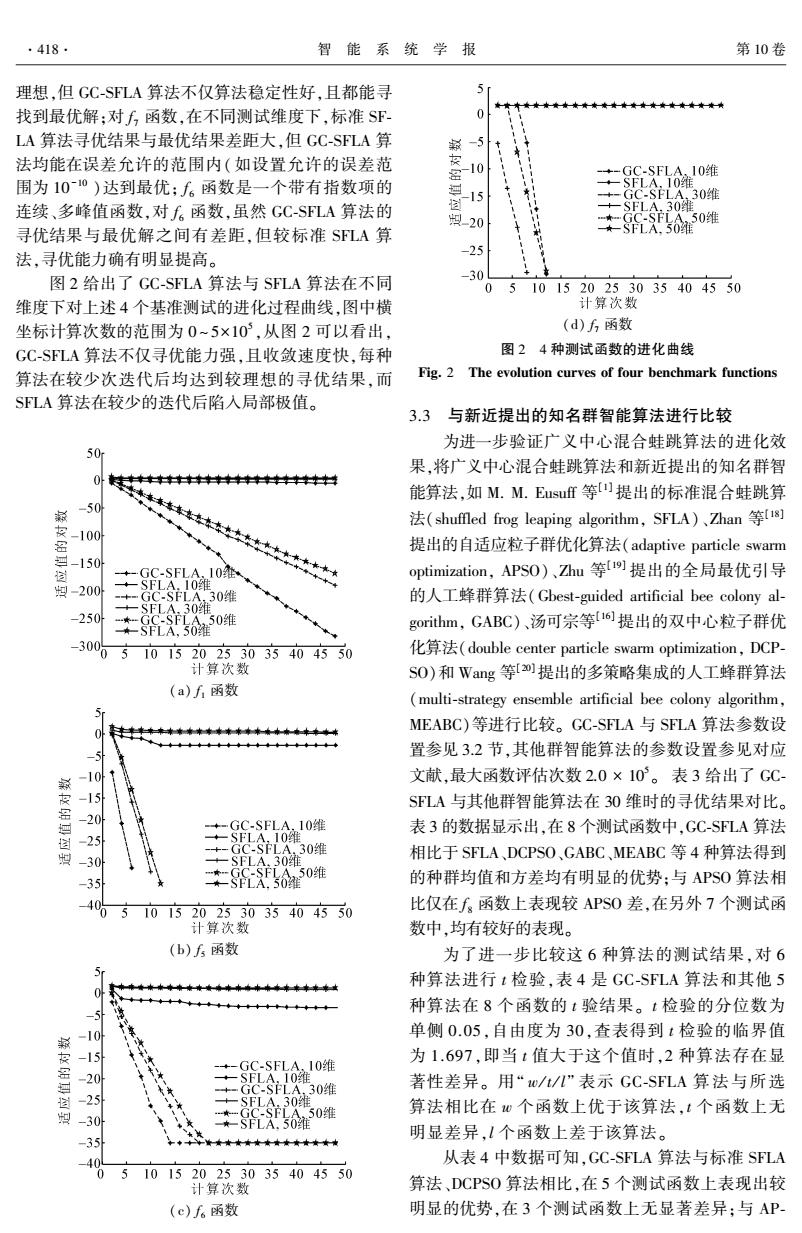
.418 智能系统学报 第10卷 理想,但GC-SFLA算法不仅算法稳定性好,且都能寻 0 ★★★★★ 找到最优解:对函数,在不同测试维度下,标准SF LA算法寻优结果与最优结果差距大,但GC-SFLA算 5 法均能在误差允许的范围内(如设置允许的误差范 -GC.SFLA10维 围为10-0)达到最优:f。函数是一个带有指数项的 0维 连续、多峰值函数,对f6函数,虽然GC-SFLA算法的 SFLA.30维 020 寻优结果与最优解之间有差距,但较标准SFLA算 法,寻优能力确有明显提高。 -25 图2给出了GC-SFLA算法与SFLA算法在不同 -30 05101520253035404550 维度下对上述4个基准测试的进化过程曲线,图中横 计算次数 坐标计算次数的范围为0~5×10,从图2可以看出, (d)f6,函数 GC-SFLA算法不仅寻优能力强,且收敛速度快,每种 图24种测试函数的进化曲线 算法在较少次迭代后均达到较理想的寻优结果,而 Fig.2 The evolution curves of four benchmark functions SFLA算法在较少的迭代后陷入局部极值。 3.3 与新近提出的知名群智能算法进行比较 为进一步验证广义中心混合蛙跳算法的进化效 50 果,将广义中心混合蛙跳算法和新近提出的知名群智 0 中牛中中中牛料 能算法,如M.M.Eusuff等提出的标准混合蛙跳算 菊 -50 法(shuffled frog leaping algorithm,SFLA)、Zhan等18] -100 提出的自适应粒子群优化算法(adaptive particle swarm -150 +-GC-SFLA,10维 optimization,APs0)、Zhu等o提出的全局最优引导 -200 -SFLA.10维 +=GC-SFLA.30维 的人工蜂群算法(Gbest-guided artificial bee colony al- +-SFLA.30维 -250 gorithm,GABC)、汤可宗等16提出的双中心粒子群优 -30065 101520253035404550 化算法(double center particle swarm optimization,DCP- 计算次数 SO)和Wang等[0提出的多策略集成的人工蜂群算法 (a)f函数 (multi-strategy ensemble artificial bee colony algorithm, MEABC)等进行比较。GC-SFLA与SFLA算法参数设 置参见3.2节,其他群智能算法的参数设置参见对应 -10t 文献,最大函数评估次数2.0×10。表3给出了GC- -15 SLA与其他群智能算法在30维时的寻优结果对比。 GC-SFLA.10维 表3的数据显示出,在8个测试函数中,GC-SFLA算法 -25 -SFLA,10维 -GC-SLA.30维 SFLA30 相比于SFLA、DCPSO、GABC、MEABC等4种算法得到 车60唯 的种群均值和方差均有明显的优势:与APSO算法相 5 101520253035404550 比仅在f函数上表现较APS0差,在另外7个测试函 计算次数 数中,均有较好的表现。 (b)5函数 为了进一步比较这6种算法的测试结果,对6 中★◆味来本本支 种算法进行t检验,表4是GC-SFLA算法和其他5 种算法在8个函数的t验结果。t检验的分位数为 -10 单侧0.05,自由度为30,查表得到t检验的临界值 -15 公米 -GC-SFLA.10维 为1.697,即当1值大于这个值时,2种算法存在显 -20 把1难0维 著性差异。用“w/L/I"”表示GC-SFLA算法与所选 一SFLA,30 蛔 车6M0唯 算法相比在w个函数上优于该算法,t个函数上无 -30 明显差异,1个函数上差于该算法。 ★★★★★★★★★★★★ 40 从表4中数据可知,GC-SFLA算法与标准SFLA 5 101520253035404550 计算次数 算法、DCPSO算法相比,在5个测试函数上表现出较 (c)f。函数 明显的优势,在3个测试函数上无显著差异:与AP
理想,但 GC⁃SFLA 算法不仅算法稳定性好,且都能寻 找到最优解;对 f 7 函数,在不同测试维度下,标准 SF⁃ LA 算法寻优结果与最优结果差距大,但 GC⁃SFLA 算 法均能在误差允许的范围内(如设置允许的误差范 围为 10 -10 )达到最优; f 6 函数是一个带有指数项的 连续、多峰值函数,对 f 6 函数,虽然 GC⁃SFLA 算法的 寻优结果与最优解之间有差距,但较标准 SFLA 算 法,寻优能力确有明显提高。 图 2 给出了 GC⁃SFLA 算法与 SFLA 算法在不同 维度下对上述 4 个基准测试的进化过程曲线,图中横 坐标计算次数的范围为 0 ~ 5×10 5 ,从图 2 可以看出, GC⁃SFLA 算法不仅寻优能力强,且收敛速度快,每种 算法在较少次迭代后均达到较理想的寻优结果,而 SFLA 算法在较少的迭代后陷入局部极值。 (a) f 1 函数 (b) f 5 函数 (c) f 6 函数 (d) f 7 函数 图 2 4 种测试函数的进化曲线 Fig. 2 The evolution curves of four benchmark functions 3.3 与新近提出的知名群智能算法进行比较 为进一步验证广义中心混合蛙跳算法的进化效 果,将广义中心混合蛙跳算法和新近提出的知名群智 能算法,如 M. M. Eusuff 等[1] 提出的标准混合蛙跳算 法(shuffled frog leaping algorithm, SFLA)、Zhan 等[18] 提出的自适应粒子群优化算法(adaptive particle swarm optimization, APSO)、Zhu 等[19] 提出的全局最优引导 的人工蜂群算法(Gbest⁃guided artificial bee colony al⁃ gorithm, GABC)、汤可宗等[16]提出的双中心粒子群优 化算法(double center particle swarm optimization, DCP⁃ SO)和 Wang 等[20]提出的多策略集成的人工蜂群算法 (multi⁃strategy ensemble artificial bee colony algorithm, MEABC)等进行比较。 GC⁃SFLA 与 SFLA 算法参数设 置参见 3.2 节,其他群智能算法的参数设置参见对应 文献,最大函数评估次数 2.0 × 10 5 。 表 3 给出了 GC⁃ SFLA 与其他群智能算法在 30 维时的寻优结果对比。 表 3 的数据显示出,在 8 个测试函数中,GC⁃SFLA 算法 相比于 SFLA、DCPSO、GABC、MEABC 等 4 种算法得到 的种群均值和方差均有明显的优势;与 APSO 算法相 比仅在 f 8 函数上表现较 APSO 差,在另外 7 个测试函 数中,均有较好的表现。 为了进一步比较这 6 种算法的测试结果,对 6 种算法进行 t 检验,表 4 是 GC⁃SFLA 算法和其他 5 种算法在 8 个函数的 t 验结果。 t 检验的分位数为 单侧 0.05,自由度为 30,查表得到 t 检验的临界值 为 1.697,即当 t 值大于这个值时,2 种算法存在显 著性差异。 用“ w / t / l” 表示 GC⁃SFLA 算法与所选 算法相比在 w 个函数上优于该算法,t 个函数上无 明显差异,l 个函数上差于该算法。 从表 4 中数据可知,GC⁃SFLA 算法与标准 SFLA 算法、DCPSO 算法相比,在 5 个测试函数上表现出较 明显的优势,在 3 个测试函数上无显著差异;与 AP⁃ ·418· 智 能 系 统 学 报 第 10 卷