
第10卷第3期 智能系统学报 Vol.10 No.3 2015年6月 CAAI Transactions on Intelligent Systems Jun.2015 D0:10.3969/j.issn.1673-4785.201408026 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.tp.20150610.1558.001.html 基于触觉序列的物体分类 马蕊123,刘华平23,孙富春23,高蒙 (1.石家庄铁道大学电气与电子工程学院,河北石家庄050043:2.清华大学计算机科学与技术系,北京100084:3.清 华大学智能技术与系统国家重点实验室,北京100084) 摘要:通过安装触觉传感器的灵巧手对物体进行抓取,可以采集到丰富的触觉序列信息。对这些触觉信息进行分 类可以显著提高机器人的环境感知和灵巧操作能力。为此,将触觉序列划分为一系列子触觉序列,使用基于线性动 态系统(LDS)的方法进行特征提取。由于使用LDS提取的特征存在于非欧式空间,在对特征进行处理时,使用与欧 式距离不同的马丁距离(Martin distance)作为量度来表征2个LDS特征之间的距离,并使用K-Medoid算法进行聚 类。而后使用聚类得到的码书表征触觉序列,完成系统包(bag-of-system)特征模型构建,并利用支持向量机(SVM) 实现高效分类。最后使用16种实验样本构建的触觉序列数据集对上述算法进行评测,获得了可观的识别效果,表明 了该算法可以用于触觉序列的物体分类。 关键词:物体分类;触觉序列;线性动态系统;系统包:马丁距离;支持向量机:K-Medoid算法 中图分类号:TP24文献标志码:A文章编号:1673-4785(2015)03-0362-07 中文引用格式:马蕊,刘华平,孙富春,等.基于触觉序列的物体分类[J].智能系统学报,2015,10(3):362-368. 英文引用格式:MA Rui,LIU Huaping,SUN Fuchun,etal.Object classification based on the tactile sequence[J].CAAI Transac- tions on Intelligent Systems,2015,10(3):362-368. Object classification based on the tactile sequence MA Rui2.3,LIU Huaping2.3,SUN Fuchun2.3,GAO Meng' (1.College of Electrical and Electronic Engineering,Shijiazhuang Railway University,Shijiazhuang 050043,China;2.Department of Computer Science and Technology,Tsinghua University,Beijing 100084.China;3.State Key Laboratory of Intelligent Technology and System,Tsinghua University,Beijing 100084,China) Abstract:A large amount of information on tactile sequences can be collected by using a dexterous hand with a tactile sensor to grasp different objects.The abilities of a robot's environmental perception and dexterous manipula- tion are significantly improved after these tactile sequences are classified.Therefore,tactile sequences are separated into a series of subgroups and features are extracted by using a method based on the linear dynamical system (LDS).Since the features extracted by LDS are located in the non-Euclidean space,when dealing with these fea- tures,the Martin distance which is a measurement different from Euclidean distance is applied to represent the dis- tance between two LDS features,and the K-Medoid algorithm is used for clustering.Then,the codebook which is formed after clustering is used to represent the tactile sequence,the model of bag-of-system is formed,and the sup- port vector machine (SVM)is used to classify these objects efficiently.Finally,a dataset based on 16 objects is used to evaluate the algorithm and the result of recognition is good,which proves this algorithm can be used in tact- ile sequences for object classification. Keywords:object classification;tactile sequence;linear dynamical system (LDS);bag-of-system;Martin dis- tance;support vector machine (SVM);K-Medoid algorithm 触觉是一种基本的感觉方式,无论对于人类自 身还是机器人,触觉信息都是与周围环境进行交流 的重要媒介。人类使用皮肤上的触觉器官来感知物 收稿日期:2014-08-20.网络出版日期:2015-06-10. 基金项目:国家“973”计划资助项目(2013CB329403):国家自然科学 体的温度,合理地抓取物品,并通过触摸来分辨视觉 基金重大国际合作研究项目(61210013). 通信作者:马蕊.E-mail:maui519@126.com. 上看似相同但材质不同的物体。对于机器人系统
第 10 卷第 3 期 智 能 系 统 学 报 Vol.10 №.3 2015 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2015 DOI:10.3969 / j.issn.1673⁃4785.201408026 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20150610.1558.001.html 基于触觉序列的物体分类 马蕊1,2,3 ,刘华平2,3 ,孙富春2,3 ,高蒙1 (1.石家庄铁道大学 电气与电子工程学院,河北 石家庄 050043;2.清华大学 计算机科学与技术系,北京 100084;3.清 华大学 智能技术与系统国家重点实验室,北京 100084) 摘 要:通过安装触觉传感器的灵巧手对物体进行抓取,可以采集到丰富的触觉序列信息。 对这些触觉信息进行分 类可以显著提高机器人的环境感知和灵巧操作能力。 为此,将触觉序列划分为一系列子触觉序列,使用基于线性动 态系统(LDS)的方法进行特征提取。 由于使用 LDS 提取的特征存在于非欧式空间,在对特征进行处理时,使用与欧 式距离不同的马丁距离(Martin distance)作为量度来表征 2 个 LDS 特征之间的距离,并使用 K⁃Medoid 算法进行聚 类。 而后使用聚类得到的码书表征触觉序列,完成系统包( bag⁃of⁃system)特征模型构建,并利用支持向量机( SVM) 实现高效分类。 最后使用 16 种实验样本构建的触觉序列数据集对上述算法进行评测,获得了可观的识别效果,表明 了该算法可以用于触觉序列的物体分类。 关键词:物体分类;触觉序列;线性动态系统;系统包;马丁距离;支持向量机;K⁃Medoid 算法 中图分类号:TP24 文献标志码:A 文章编号:1673⁃4785(2015)03⁃0362⁃07 中文引用格式:马蕊,刘华平,孙富春,等. 基于触觉序列的物体分类[J]. 智能系统学报, 2015, 10(3): 362⁃368. 英文引用格式:MA Rui, LIU Huaping, SUN Fuchun, et al. Object classification based on the tactile sequence[J]. CAAI Transac⁃ tions on Intelligent Systems, 2015, 10(3): 362⁃368. Object classification based on the tactile sequence MA Rui 1,2,3 , LIU Huaping 2,3 , SUN Fuchun 2,3 , GAO Meng 1 (1. College of Electrical and Electronic Engineering, Shijiazhuang Railway University, Shijiazhuang 050043, China; 2. Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China; 3. State Key Laboratory of Intelligent Technology and System, Tsinghua University, Beijing 100084, China) Abstract:A large amount of information on tactile sequences can be collected by using a dexterous hand with a tactile sensor to grasp different objects. The abilities of a robot's environmental perception and dexterous manipula⁃ tion are significantly improved after these tactile sequences are classified. Therefore, tactile sequences are separated into a series of subgroups and features are extracted by using a method based on the linear dynamical system (LDS). Since the features extracted by LDS are located in the non⁃Euclidean space, when dealing with these fea⁃ tures, the Martin distance which is a measurement different from Euclidean distance is applied to represent the dis⁃ tance between two LDS features, and the K⁃Medoid algorithm is used for clustering. Then, the codebook which is formed after clustering is used to represent the tactile sequence, the model of bag⁃of⁃system is formed, and the sup⁃ port vector machine (SVM) is used to classify these objects efficiently. Finally, a dataset based on 16 objects is used to evaluate the algorithm and the result of recognition is good, which proves this algorithm can be used in tact⁃ ile sequences for object classification. Keywords:object classification; tactile sequence; linear dynamical system ( LDS); bag⁃of⁃system; Martin dis⁃ tance; support vector machine (SVM); K⁃Medoid algorithm 收稿日期:2014⁃08⁃20. 网络出版日期:2015⁃06⁃10. 基金项目:国家“973”计划资助项目(2013CB329403);国家自然科学 基金重大国际合作研究项目(61210013). 通信作者:马蕊. E⁃mail: marui519@ 126.com. 触觉是一种基本的感觉方式,无论对于人类自 身还是机器人,触觉信息都是与周围环境进行交流 的重要媒介。 人类使用皮肤上的触觉器官来感知物 体的温度,合理地抓取物品,并通过触摸来分辨视觉 上看似相同但材质不同的物体。 对于机器人系统

第3期 马蕊,等:基于触觉序列的物体分类 ·363· 触觉信息可以帮助机器人完成检查和控制物体摆放 以实现全局类别界定,因此,需将触觉序列分为一系 位置、识别抓取物体等任务,这对于实现机器人的外 列子序列,并对每组子触觉序列进行特征提取。参 部环境探索和对物体的操控,有着极其重要的意义。 照文献[13]中的方法对触觉序列进行分段处理,其 迄今为止,人们对机器人感知,包括基于触觉的 中子序列分段个数d与窗函数宽度L会影响分类准 抓取稳定性、目标分类等方面进行了广泛而深入的 确率,这将在实验验证部分详细介绍。 研究,特别是人工智能的理论研究方法在机器人领 众所周知,具有任意协方差的二阶系统可用零均 域取得了巨大的成就四。文献[2]中对机器人情感 值高斯白噪声驱动的线性动态系统进行建模。对 描述模型进行了研究。文献[3]描述了安装胡须型 于任意一组子触觉序列y(t),定义其为一组触觉观 触觉传感器的移动机器人进行目标定位和目标抓取 测序列,并有{y(t)∈9}:=1,p为触觉序列维数,t 的过程。在文献[4]中,作者通过使用灵巧手对大 为触觉序列采样时间,使用y(t)进行触觉建模。 量物体抓取的仿真实验,提供了一个可以对抓取稳 假设存在正整数n、对称正定矩阵Q∈xm和 定性进行预测的数据集合。文献[5-6]使用Schunk R∈9,则有 三指和两指灵巧手对一系列物体进行抓取,并对抓 (x(t+1)=Ax(t)+Bv(t);x(0)=xo (1) 取数据使用隐马尔科夫模型(hidden mark models,. ly(t)=Cx(t)+w(t) HMMs)方法进行处理,实现对抓取稳定性的判断。 式中:x(t)∈P为t时刻的隐状态序列;A为隐状态 文献[7]中,作者将自制触觉传感器安装在Schunk 动态矩阵,C为系统的隐状态输出矩阵,且满足A∈ 二指灵巧手手指两端,对刚性和非刚性物体进行抓 x”,C∈Pn;w(t)与Bv(t)分别表示估计值和 取实验,使用触觉信息对抓取物体进行分类。文献 状态噪声,并且满足Bv(t)~N(0,Q),w(t)~ [8]使用综合稀疏编码算法(spatio-temporal online N(0,R)。 recursive kernel Gaussian process,STORK-GP)5 文献[15]中已经验证元组(A,C)可以体现动 指iCb机器人灵巧手触觉进行采样数据以及目标 态序列的时间特性与空间特性,结合文献[12]中基 分类预测和不确定性估计。文献[9]使用神经网络 于LDS的建模方法,本文也选用观测序列的元组 方法对物体的触觉数据进行分类,与文献[10]中使 (A,C)表征动态系统的特性。但由于实验中触觉 用提取特征来组成模型袋来进行物体的分类有着很 数据集样本的观测序列的维数p=24较高,上述计 大的区别。另外,文献[11]中描述了使用C4.5算法 算过程会比较复杂,因此对观测序列进行主成分分 对触觉数据进行处理以实现物体分类。 析(principal component analysis,PCA)降维。由图I 对触觉信息建模的工具为线性动态系统(linear 所示的PCA衰减曲线可知,随着维数不断增加,系 dynamical system,LDS)2],该模型使用欧几里德距 统主成分含量随之减少,选取主成分含量约为90% 离作为LDS的距离量度,用于触觉建模。由于LDS 时所对应的维数作为降维处理后的维数,即m=5。 并非存在于欧式空间,因此该方法具有较强的局限 100r 性。为解决上述问题,本文使用可对LDS进行充分 80 刻画的Martin距离作为量度工具,采用机器学习领 域中流行的Bag-of-Words框架对触觉数据进行分 60 析,并且将其与LDS相结合构建了Bag-of-System框 40 架,最后进行实验验证。另外本文构建了由16种实 20 验样本组成的触觉数据集,与国外同类研究中的触 觉数据集规模相比有一定优势。 0 10152025 维数 1触觉序列分类 图1主成分衰减曲线 本节将详细描述提取LDS特征、完成码书组 Fig.I Decaying curve of principle component 建、最终将得到的触觉序列系统包模型与物体标签 使用奇异值分解(single value decomposition, 送入SVM中训练分类器的方法。 SVD)对降维处理后的观测序列进行计算: 1.1LDS建模 Y=UΣv (2) 基于触觉序列的分类方法是通过局部特征提取
触觉信息可以帮助机器人完成检查和控制物体摆放 位置、识别抓取物体等任务,这对于实现机器人的外 部环境探索和对物体的操控,有着极其重要的意义。 迄今为止,人们对机器人感知,包括基于触觉的 抓取稳定性、目标分类等方面进行了广泛而深入的 研究,特别是人工智能的理论研究方法在机器人领 域取得了巨大的成就[1] 。 文献[2]中对机器人情感 描述模型进行了研究。 文献[3]描述了安装胡须型 触觉传感器的移动机器人进行目标定位和目标抓取 的过程。 在文献[4]中,作者通过使用灵巧手对大 量物体抓取的仿真实验,提供了一个可以对抓取稳 定性进行预测的数据集合。 文献[5-6]使用 Schunk 三指和两指灵巧手对一系列物体进行抓取,并对抓 取数据使用隐马尔科夫模型( hidden mark models, HMMs)方法进行处理,实现对抓取稳定性的判断。 文献[7]中,作者将自制触觉传感器安装在 Schunk 二指灵巧手手指两端,对刚性和非刚性物体进行抓 取实验,使用触觉信息对抓取物体进行分类。 文献 [8]使用综合稀疏编码算法( spatio⁃temporal online recursive kernel Gaussian process, STORK⁃GP) 对 5 指 iCub 机器人灵巧手触觉进行采样数据以及目标 分类预测和不确定性估计。 文献[9]使用神经网络 方法对物体的触觉数据进行分类,与文献[10]中使 用提取特征来组成模型袋来进行物体的分类有着很 大的区别。 另外,文献[11]中描述了使用 C4.5 算法 对触觉数据进行处理以实现物体分类。 对触觉信息建模的工具为线性动态系统(linear dynamical system, LDS) [12] ,该模型使用欧几里德距 离作为 LDS 的距离量度,用于触觉建模。 由于 LDS 并非存在于欧式空间,因此该方法具有较强的局限 性。 为解决上述问题,本文使用可对 LDS 进行充分 刻画的 Martin 距离作为量度工具,采用机器学习领 域中流行的 Bag⁃of⁃Words 框架对触觉数据进行分 析,并且将其与 LDS 相结合构建了 Bag⁃of⁃System 框 架,最后进行实验验证。 另外本文构建了由 16 种实 验样本组成的触觉数据集,与国外同类研究中的触 觉数据集规模相比有一定优势。 1 触觉序列分类 本节将详细描述提取 LDS 特征、完成码书组 建、最终将得到的触觉序列系统包模型与物体标签 送入 SVM 中训练分类器的方法。 1.1 LDS 建模 基于触觉序列的分类方法是通过局部特征提取 以实现全局类别界定,因此,需将触觉序列分为一系 列子序列,并对每组子触觉序列进行特征提取。 参 照文献[13]中的方法对触觉序列进行分段处理,其 中子序列分段个数 d 与窗函数宽度 L 会影响分类准 确率,这将在实验验证部分详细介绍。 众所周知,具有任意协方差的二阶系统可用零均 值高斯白噪声驱动的线性动态系统进行建模[14] 。 对 于任意一组子触觉序列 y(t) ,定义其为一组触觉观 测序列,并有 {y(t) ∈ R p } τ t = 1 , p 为触觉序列维数, t 为触觉序列采样时间,使用 y(t) 进行触觉建模。 假设存在正整数 n 、对称正定矩阵 Q ∈ R n×n 和 R ∈ R p×p ,则有 x(t + 1) = Ax(t) + Bv(t);x(0) = x0 y(t) = Cx(t) + w(t) { (1) 式中: x(t) ∈R p 为 t 时刻的隐状态序列; A 为隐状态 动态矩阵, C 为系统的隐状态输出矩阵,且满足 A ∈ R n×n , C ∈ R p×n ; w(t) 与 Bv(t) 分别表示估计值和 状态噪声,并且满足 Bv(t) ~ N(0,Q) , w(t) ~ N(0,R) 。 文献[15]中已经验证元组 (A,C) 可以体现动 态序列的时间特性与空间特性,结合文献[12]中基 于 LDS 的建模方法,本文也选用观测序列的元组 (A,C) 表征动态系统的特性。 但由于实验中触觉 数据集样本的观测序列的维数 p = 24 较高,上述计 算过程会比较复杂,因此对观测序列进行主成分分 析(principal component analysis, PCA)降维。 由图 1 所示的 PCA 衰减曲线可知,随着维数不断增加,系 统主成分含量随之减少,选取主成分含量约为 90% 时所对应的维数作为降维处理后的维数,即 m = 5。 图 1 主成分衰减曲线 Fig. 1 Decaying curve of principle component 使用奇异值分解 ( single value decomposition, SVD)对降维处理后的观测序列进行计算: Y = UΣV T (2) 第 3 期 马蕊,等:基于触觉序列的物体分类 ·363·

·364 智能系统学报 第10卷 式中:U∈mm,V∈x”,对角矩阵∑= 距离矩阵: diag(01,02,…,n),0:表示第i个奇异值。 D=Idv(MM)=d) 系统状态参数C与X的估计值为C=U,X= 式中:m表征所有的子触觉序列。 V,其中,X={x(1),x(2),…,x(r)}, 1.2.2聚类 {x(t)}=1为t时刻的隐状态序列。 聚类是码书构建过程中不可或缺的一部分,且 使用最小方差法计算隐状态动态矩阵A: 聚类中心个数k的选取直接影响数据分类的准确 A= 性。K-Means与K-Medoid是2种常用的聚类算法。 [x(2)x(3)·x(r)][x(1)x(2)…x(r-1)] 由于使用K-Means算法需要将上述马丁距离转换为 (3) 欧式距离后进行运算,而K-Medoid算法可以直接使 式中:t表示Moore-Penrose广义逆。 用马丁距离进行运算,因此,选用K-Medoid算法进 就此完成了触觉序列的特征提取,得到一系列 行聚类。 观测矩阵元组(A,C)。但这种特征不能作为特征 K-Medoid算法首先在数据中选取一些点作 向量直接送入SVM中训练分类器,还需对其进行后 为聚类中心,剩余的点根据与聚类中心点的距离 续处理。 进行分组。聚类中心可以作为数据平面的中心 1.2码书组建 点,其选取遵循该点与其他数据点的平方距离和 1.2.1马丁距离 最小这一原则,这种距离可以为马丁距离、欧式 对于提取的特征存在于欧式空间的分类算法, 距离或者其他距离。 其特征之间的距离需使用欧式距离来衡量。然而,2 使用K-Medoid算法对马丁距离矩阵D进行聚 组LDS特征M1=(A1,C1)、M2=(A2,C2)存在于 类后,得到由LDS特征组建的码书{M;1,其中k 非欧式空间中,参照文献[16]中的方法,使用马丁 为聚类中心个数,每组LDS特征被称为码词(Code 距离来衡量LDS之间的距离。 word)。 马丁距离是基于2个系统之间的空间角定义 1.3系统包模型 的,这种空间角又称为观测子序列模型参数的规则 使用码书对触觉序列表征得到系统包模型 角(principle angles)。在系统中,即为LDS特征之 {BoS()1。这种表征方式外部体现为直方图模 间的规则角,定义为 型h=[h,h2…h.]T∈m,可由特征词频率 9(M)=[CCA(CA2)T…]∈x(4) (term frequency,TF)算法得到。 式中:A为隐状态动态矩阵,C为系统的隐状态输 假设在第i组触觉序列中,第j组码词出现的次 出矩阵,9(M)表示特征之间的规则角。 数为c次,则有 对于任意2个模型之间规则角的计算,首先使 C可 用李雅普方程求解P矩阵: g=yti=1,2,…mj=1,2,…,k(8》) APO-P=-CC (5) 式中:h:表示在第i组触觉序列中,第j组码词出现 式中: 的频率,m为触觉序列个数,k为聚类中心点个数。 (Pi P12 P= ∈9升2nx2n h,=[hih2…hk]为一组特征向量。 经过上述过程,得到触觉序列系统包,它由m (Au 0 组特征向量组成,可与物体标签一起送入SVM中训 A= ∈2mx2 0A2 练分类器。 C=[C,C2]∈9x2a 1.4分类器设计 然后使用式(6)计算子空间角{0:}:,的余弦值: 支持向量机作为一种高准确率的分类工具,被 cos'0:eigenvalue;(Pi P2 P22 P2)(6) 广泛应用于物体识别与分类等领域7-11。SVM分 最终得到特征M与M2之间的马丁距离dw(M1,M2): 类器既可以直接进行二分类,也可以完成多分类任 务。输入SVM中的样本规定为{h,l,}1形式,式 d,(M,M,)2=-nos0, (7) 中h:为特征向量,l表示第i个特征向量对应标签, 使用上述方法进行计算后,得到特征间的马丁 m为特征向量个数,也为触觉序列个数
式中: U ∈ R m×n , V ∈ R τ ×n , 对 角 矩 阵 Σ = diag σ1 ,σ2 ,...,σn ( ) , σi 表示第 i 个奇异值。 系统状态参数 C 与 X 的估计值为 C ^ = U , X ^ = ΣV T , 其 中, X ^ = {x(1),x(2),…,x(τ)} , {x(t)} τ t = 1 为 t 时刻的隐状态序列。 使用最小方差法计算隐状态动态矩阵 A : A = [x(2) x(3) … x(τ)][x(1) x(2) … x(τ - 1)] † (3) 式中:† 表示 Moore⁃Penrose 广义逆。 就此完成了触觉序列的特征提取,得到一系列 观测矩阵元组 (A,C) 。 但这种特征不能作为特征 向量直接送入 SVM 中训练分类器,还需对其进行后 续处理。 1.2 码书组建 1.2.1 马丁距离 对于提取的特征存在于欧式空间的分类算法, 其特征之间的距离需使用欧式距离来衡量。 然而,2 组 LDS 特征 M1 = (A1 ,C1 ) 、 M2 = (A2 ,C2 ) 存在于 非欧式空间中,参照文献[16] 中的方法,使用马丁 距离来衡量 LDS 之间的距离。 马丁距离是基于 2 个系统之间的空间角定义 的,这种空间角又称为观测子序列模型参数的规则 角(principle angles)。 在系统中,即为 LDS 特征之 间的规则角,定义为 ϑ¥(M) = [C CA (C A 2 ) T …] ∈ R ¥×n (4) 式中: A 为隐状态动态矩阵, C 为系统的隐状态输 出矩阵, ϑ¥(M) 表示特征之间的规则角。 对于任意 2 个模型之间规则角的计算,首先使 用李雅普方程求解 P 矩阵: A TPQ - P = - C TC (5) 式中: P = P11 P12 P21 P22 æ è çç ö ø ÷÷ ∈ R 2n×2n A = A11 0 0 A22 æ è çç ö ø ÷÷ ∈ R 2n×2n C = [C1 C2 ] ∈ R p×2n 然后使用式(6)计算子空间角 θi { } n i = 1 的余弦值: cos 2 θi = eigenvaluei(P -1 11 P12 P -1 22 P21 ) (6) 最终得到特征 M1 与 M2 之间的马丁距离 dM(M1,M2) : dM (M1 ,M2 ) 2 = - ln∏ n i = 1 cos 2 θi (7) 使用上述方法进行计算后,得到特征间的马丁 距离矩阵: D = {dM(Mi,Mj)} i = md ,j = md i = 1,j = 1 = dij { } i = md ,j = md i = 1,j = 1 式中: md 表征所有的子触觉序列。 1.2.2 聚类 聚类是码书构建过程中不可或缺的一部分,且 聚类中心个数 k 的选取直接影响数据分类的准确 性。 K⁃Means 与 K⁃Medoid 是 2 种常用的聚类算法。 由于使用 K⁃Means 算法需要将上述马丁距离转换为 欧式距离后进行运算,而 K⁃Medoid 算法可以直接使 用马丁距离进行运算,因此,选用 K⁃Medoid 算法进 行聚类。 K⁃Medoid 算法首先在数据中选取一些点作 为聚类中心,剩余的点根据与聚类中心点的距离 进行分组。 聚类中心可以作为数据平面的中心 点,其选取遵循该点与其他数据点的平方距离和 最小这一原则,这种距离可以为马丁距离、欧式 距离或者其他距离。 使用 K⁃Medoid 算法对马丁距离矩阵 D 进行聚 类后,得到由 LDS 特征组建的码书 {Mi} k i = 1 ,其中 k 为聚类中心个数,每组 LDS 特征被称为码词(Code⁃ word)。 1.3 系统包模型 使用码书对触觉序列表征得到系统包模型 {BoS(i) } m i = 1 。 这种表征方式外部体现为直方图模 型 h = [h1 h2 … hm ] T ∈ R m ,可由特征词频率 (term frequency, TF)算法得到。 假设在第 i 组触觉序列中,第 j 组码词出现的次 数为 cij 次,则有 hij = cij ∑ k j = 1 cij ,i = 1,2,…,m,j = 1,2,…,k (8) 式中: hij 表示在第 i 组触觉序列中,第 j 组码词出现 的频率, m 为触觉序列个数, k 为聚类中心点个数。 h1 = [h11 h12 … h1k] 为一组特征向量。 经过上述过程,得到触觉序列系统包,它由 m 组特征向量组成,可与物体标签一起送入 SVM 中训 练分类器。 1.4 分类器设计 支持向量机作为一种高准确率的分类工具,被 广泛应用于物体识别与分类等领域[17-18] 。 SVM 分 类器既可以直接进行二分类,也可以完成多分类任 务。 输入 SVM 中的样本规定为 {hi,l i} m i = 1 形式,式 中 hi 为特征向量, l i 表示第 i 个特征向量对应标签, m 为特征向量个数,也为触觉序列个数。 ·364· 智 能 系 统 学 报 第 10 卷

第3期 马蕊,等:基于触觉序列的物体分类 ·365· SVM使用线性核函数{ohIc∈业}创建一组 2实验结果与分析 超平面来完成线性数据二分类,式中ω。为权重向 2.1数据采集 量,也为超平面的法向量,并将分类问题转换为最优 实验使用BH8-280三指灵巧手对16种日常用 化问题: 品进行抓取。如图3所示,实验物品分别为橙色圆 mjnJ.)=.+C(9) 筒、咖啡杯、可乐瓶、瓦力玩具、粉色杯子、企鹅玩偶 熊猫玩偶、塑料三角、透明圆筒、灰色圆筒、红纸盒、 式中:参数C可由交叉验证获得,L(ω。;,h:)称为 白色纸筒、金色海绵圆筒、褐色海绵圆筒、牛奶盒和 损耗函数,可由式(10)进行定义。 金色海绵块。 L(w.;,h:)=[max(0,w·-1)]2(10) 对于多分类问题,SVM使用+1标记属于该类别 的样本,而使用-1进行标记不属于该类别的样本,并 采用“一对多”的方法,设置一系列子分类器训练分类 器,分别计算各个子分类器的决策函数值,选取最大 函数值所对应的类别作为测试数据的标签: hm=max h (11) 基于核函数的SVM适用于样本非线性的情况。 使用径向基核函数(radial basis function, RBF)k(h1,h2)=exp[-y×d(h,h2)]进行数据 图3实验物品 分类,其中y为自由参数,d(h,h2)表示特征向量 Fig.3 Experiment objects 之间的距离。 对于每一种实验物体,进行50次抓取实验,抓 1.5算法流程 取方式参照文献[12],灵巧手手掌分别与物体上 如图2所示,算法流程步骤如下: 部、中部和底部的不同部位进行接触。图4为企鹅 1)将每组触觉序列分为d组触觉子序列,使用 玩偶与灵巧手手掌接触方式示意图。 LDS模型对每组子序列进行建模,分别提取子触觉 序列的特征M。 2)使用马丁距离计算动态特征之间的距离,并 使用K-Medoid算法进行聚类,组建码书。 2 3)使用码书对每组触觉序列进行表征,得到每 组触觉序列的字典(bag-of-word,BoW),所有字典 (a)顶部抓取 (b)中部抓取1 组成“系统包”(bag-of-system,BoS)模型。 4)将系统包与物体标签一起送入SVM训练分 类器。 5)对测试序列进行分类预测时,重复上述过 程,送入分类器即可得到物体的标签。 (c)中部抓取2 (d)底部抓取 图4抓取位姿 码书 系统包 Fig.4 Grasping poses 触觉序列1 子触觉序列 马】亞肉 表征 触觉序到 手掌在抓取不同物体时,实验物体的材质、形状 6.",3 等物理信息会使触觉信息产生差异,这种差异可以 调链 作为物体识别和分类的依据[]。选取8种物体的 子觉序列 陶试序列 分类智1 白白白→可-M器 触觉序列进行触觉图像绘制,如图5所示,不同物体 的抓取图像有明显差异。 图2算法流程 对触觉序列进行数据处理,选取稳定阶段的触 Fig.2 The work flow of our method 觉序列进行分析,将每组样本长度限定为500个样
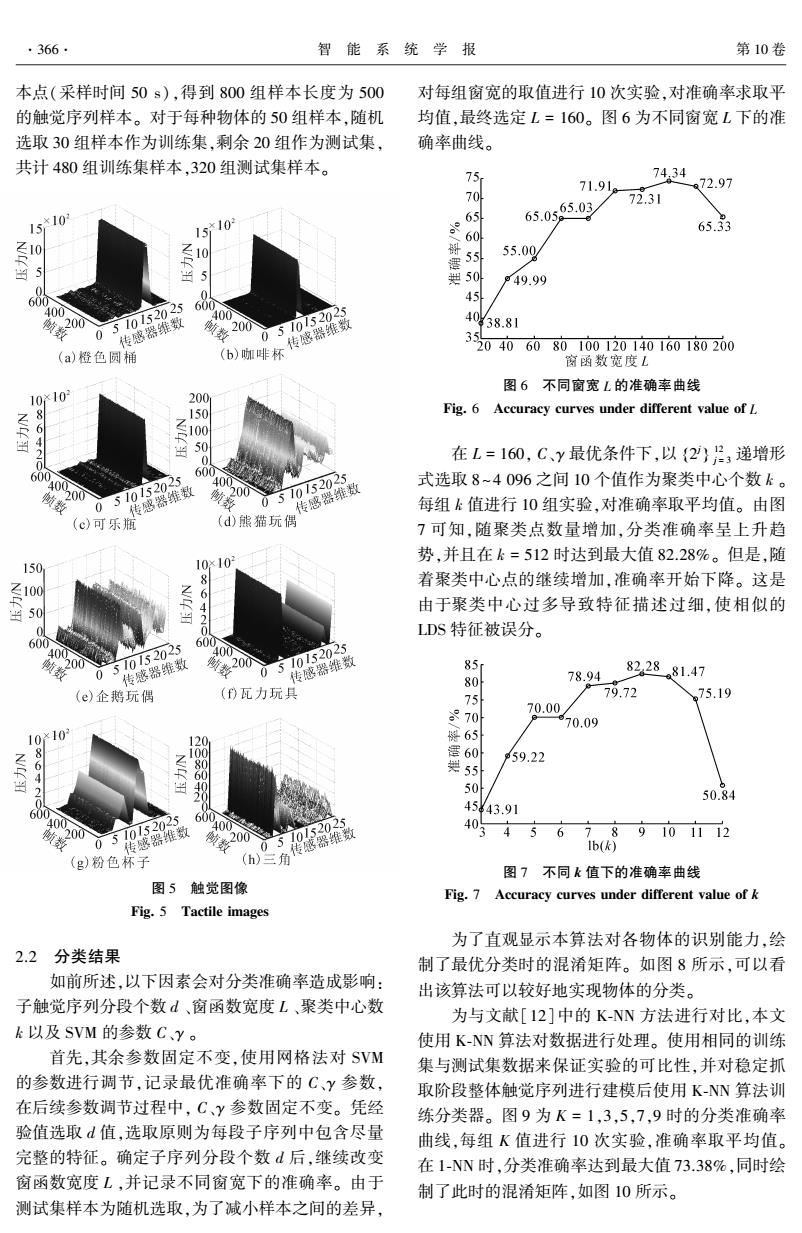
SVM 使用线性核函数 {ω T c h | c ∈ ψ} 创建一组 超平面来完成线性数据二分类,式中 ωc 为权重向 量,也为超平面的法向量,并将分类问题转换为最优 化问题: min ωc {J(ωc) = ‖ ωc‖2 2 + C∑ m i = 1 L(ωc;l c i ,hi)}(9) 式中:参数 C 可由交叉验证获得, L(ωc;l c i ,hi) 称为 损耗函数,可由式(10)进行定义。 L(ωc;l c i ,hi) = [max(0,ω T c ·l c i - 1)] 2 (10) 对于多分类问题,SVM 使用+1 标记属于该类别 的样本,而使用-1 进行标记不属于该类别的样本,并 采用“一对多”的方法,设置一系列子分类器训练分类 器,分别计算各个子分类器的决策函数值,选取最大 函数值所对应的类别作为测试数据的标签: l test = max c∈ψ ω T c htest (11) 基于核函数的 SVM 适用于样本非线性的情况。 使 用 径 向 基 核 函 数 ( radial basis function, RBF) κ(h1 ,h2 ) = exp [ - γ × d(h1 ,h2 ) ] 进行数据 分类,其中 γ 为自由参数, d(h1 ,h2 ) 表示特征向量 之间的距离。 1.5 算法流程 如图 2 所示,算法流程步骤如下: 1)将每组触觉序列分为 d 组触觉子序列,使用 LDS 模型对每组子序列进行建模,分别提取子触觉 序列的特征 M 。 2)使用马丁距离计算动态特征之间的距离,并 使用 K⁃Medoid 算法进行聚类,组建码书。 3)使用码书对每组触觉序列进行表征,得到每 组触觉序列的字典( bag⁃of⁃word, BoW),所有字典 组成“系统包”(bag⁃of⁃system, BoS)模型。 4)将系统包与物体标签一起送入 SVM 训练分 类器。 5)对测试序列进行分类预测时,重复上述过 程,送入分类器即可得到物体的标签。 图 2 算法流程 Fig. 2 The work flow of our method 2 实验结果与分析 2.1 数据采集 实验使用 BH8⁃280 三指灵巧手对 16 种日常用 品进行抓取。 如图 3 所示,实验物品分别为橙色圆 筒、咖啡杯、可乐瓶、瓦力玩具、粉色杯子、企鹅玩偶、 熊猫玩偶、塑料三角、透明圆筒、灰色圆筒、红纸盒、 白色纸筒、金色海绵圆筒、褐色海绵圆筒、牛奶盒和 金色海绵块。 图 3 实验物品 Fig. 3 Experiment objects 对于每一种实验物体,进行 50 次抓取实验,抓 取方式参照文献[12],灵巧手手掌分别与物体上 部、中部和底部的不同部位进行接触。 图 4 为企鹅 玩偶与灵巧手手掌接触方式示意图。 图 4 抓取位姿 Fig. 4 Grasping poses 手掌在抓取不同物体时,实验物体的材质、形状 等物理信息会使触觉信息产生差异,这种差异可以 作为物体识别和分类的依据[19] 。 选取 8 种物体的 触觉序列进行触觉图像绘制,如图 5 所示,不同物体 的抓取图像有明显差异。 对触觉序列进行数据处理,选取稳定阶段的触 觉序列进行分析,将每组样本长度限定为 500 个样 第 3 期 马蕊,等:基于触觉序列的物体分类 ·365·
·366 智能系统学报 第10卷 本点(采样时间50s),得到800组样本长度为500 对每组窗宽的取值进行10次实验,对准确率求取平 的触觉序列样本。对于每种物体的50组样本,随机 均值,最终选定L=160。图6为不同窗宽L下的准 选取30组样本作为训练集,剩余20组作为测试集, 确率曲线。 共计480组训练集样本,320组测试集样本。 75 7434 71.91g 72.97 70 72.31 ×10 6 65.0565.03 15 15S10 60, 65房 N/ 55 55.00 5 装504 °49.99 60 0 45 400 0310152025 0 200 400 传感器维数 0510152025 (a)橙色圆 咖华杯传感器维数 多20 40Y38.81 20406080100120140160180200 窗函数宽度 图6不同窗宽L的准确率曲线 1010 200 8 150 Fig.6 Accuracy curves under different value of L 100 42 在L=160,C、y最优条件下,以(2),递增形 60 60 200 帧数 了10152025 400 式选取8~4096之间10个值作为聚类中心个数k。 0 传感器维数 0310152025 传感器维数 每组k值进行10组实验,对准确率取平均值。由图 (c)可乐 (d)熊猫玩 7可知,随聚类点数量增加,分类准确率呈上升趋 势,并且在k=512时达到最大值82.28%。但是,随 150 10×102 着聚类中心点的继续增加,准确率开始下降。这是 6 50 由于聚类中心过多导致特征描述过细,使相似的 LDS特征被误分。 600 0310152025 60 0 400 20入100 400 传感器维数 传感器维数 85 8 78.94 822881.47 (e)企鹅玩偶 ()瓦力玩 75 79.72 75.19 97 70.00 70.09 10 103 120 解65 8642 澤60 聪55 59.22 50h 50.84 60 45¥43.91 40 0310152025 传感器维数 000 40 20 456 789101112 Ib() (g)粉色杯 h)三角 图7不同k值下的准确率曲线 图5触觉图像 Fig.7 Accuracy curves under different value of k Fig.5 Tactile images 为了直观显示本算法对各物体的识别能力,绘 2.2分类结果 制了最优分类时的混淆矩阵。如图8所示,可以看 如前所述,以下因素会对分类准确率造成影响: 出该算法可以较好地实现物体的分类。 子触觉序列分段个数d、窗函数宽度L、聚类中心数 为与文献[12]中的K-NN方法进行对比,本文 k以及SVM的参数Cy。 使用K-NN算法对数据进行处理。使用相同的训练 首先,其余参数固定不变,使用网格法对SVM 集与测试集数据来保证实验的可比性,并对稳定抓 的参数进行调节,记录最优准确率下的C、y参数, 取阶段整体触觉序列进行建模后使用K-NN算法训 在后续参数调节过程中,C、y参数固定不变。凭经 练分类器。图9为K=1,3,5,7,9时的分类准确率 验值选取d值,选取原则为每段子序列中包含尽量 曲线,每组K值进行10次实验,准确率取平均值。 完整的特征。确定子序列分段个数d后,继续改变 在1-NN时,分类准确率达到最大值73.38%,同时绘 窗函数宽度L,并记录不同窗宽下的准确率。由于 制了此时的混淆矩阵,如图10所示。 测试集样本为随机选取,为了减小样本之间的差异
本点(采样时间 50 s),得到 800 组样本长度为 500 的触觉序列样本。 对于每种物体的 50 组样本,随机 选取 30 组样本作为训练集,剩余 20 组作为测试集, 共计 480 组训练集样本,320 组测试集样本。 图 5 触觉图像 Fig. 5 Tactile images 2.2 分类结果 如前所述,以下因素会对分类准确率造成影响: 子触觉序列分段个数 d 、窗函数宽度 L 、聚类中心数 k 以及 SVM 的参数 C、γ 。 首先,其余参数固定不变,使用网格法对 SVM 的参数进行调节,记录最优准确率下的 C、γ 参数, 在后续参数调节过程中, C、γ 参数固定不变。 凭经 验值选取 d 值,选取原则为每段子序列中包含尽量 完整的特征。 确定子序列分段个数 d 后,继续改变 窗函数宽度 L ,并记录不同窗宽下的准确率。 由于 测试集样本为随机选取,为了减小样本之间的差异, 对每组窗宽的取值进行 10 次实验,对准确率求取平 均值,最终选定 L = 160。 图 6 为不同窗宽 L 下的准 确率曲线。 图 6 不同窗宽 L 的准确率曲线 Fig. 6 Accuracy curves under different value of L 在 L = 160, C、γ 最优条件下,以 2 j { } 12 j = 3 递增形 式选取 8~4 096 之间 10 个值作为聚类中心个数 k 。 每组 k 值进行 10 组实验,对准确率取平均值。 由图 7 可知,随聚类点数量增加,分类准确率呈上升趋 势,并且在 k = 512 时达到最大值 82.28%。 但是,随 着聚类中心点的继续增加,准确率开始下降。 这是 由于聚类中心过多导致特征描述过细,使相似的 LDS 特征被误分。 图 7 不同 k 值下的准确率曲线 Fig. 7 Accuracy curves under different value of k 为了直观显示本算法对各物体的识别能力,绘 制了最优分类时的混淆矩阵。 如图 8 所示,可以看 出该算法可以较好地实现物体的分类。 为与文献[12]中的 K⁃NN 方法进行对比,本文 使用 K⁃NN 算法对数据进行处理。 使用相同的训练 集与测试集数据来保证实验的可比性,并对稳定抓 取阶段整体触觉序列进行建模后使用 K⁃NN 算法训 练分类器。 图 9 为 K = 1,3,5,7,9 时的分类准确率 曲线,每组 K 值进行 10 次实验,准确率取平均值。 在 1⁃NN 时,分类准确率达到最大值 73.38%,同时绘 制了此时的混淆矩阵,如图 10 所示。 ·366· 智 能 系 统 学 报 第 10 卷