
省领精品课程—材料力学 共次,计算外力功=一P听。 最后,应用功能原理,=界,即 品以 由此得到 f为正值,表示与P的方向相同。 由本例看到,应用功能原理能方使地求出位移。但是,直接应用功能原理计算位移也会 遇到麻烦,例如,若计算D点的挠度,该点处没有集中力,无法应用功能原理:又例如,若 将跨中的集中力P去掉,换成均布载荷下的简支梁,跨中的挠度也不能直接由功能原理 出:还有,若本例的简支梁上同时有两个或两个以上载荷,想用功能原理求跨中挠度也显得 无能为力了。为解决这类问题,应继续分析能量原理。 §13.2莫尔定理 R=1 (b) ce) 图13-7 设在载荷P、P、P、P…作用下,梁的弯矩是M(x),梁的变形能是 (a) 根据前一节的分析,直接应用功能原理还无法求出任意点C的挠度£,为此必须另找出路 设在上述一组载荷作用之前,先在C点沿f方向作用一个单位力P1,如图13-7(b》所示 这时梁的弯矩记为M(x),梁的变形能是 (b) 在已经有了P后,再把原来的一组载荷P、P、P、…作用到梁上,见图13-7(c)。对于线 弹性结构,计算变形可应用叠加原理。于是,虽然先有P作用,载荷P、P、P…在它们各 自的位移上所做的功仍然等于变形能U,即()式。但是,由于P。1己在梁上,故它在位 移f上做功Pf=1·f。这样一来,按先作用P再作用P、P、P、…的次序加载,染的变形 能是 (e) 另一方面,在P和P、P、P、…的共同作用下,梁的弯矩为(x)+W(),梁的变形 This document is generated by trial version of Print2Flash (www.print2flash.com)

省级精品课程 一材料力学 能为 M(M d (d) 2EI. (c)、(d)两式应相等: stI·f可,G+aM国 (e) 展开(e)式右边,并利用(a)、(b)两式,得 1·MCM.达 (13-10) EI 这就是计算挠度的莫尔定理。又称为莫尔积分。利用莫尔定理计算位移时,必须在指定点及 指定方向上假想地加一个单位力,所以这个方法又称为单位力(载荷)法。公式(13-10) 的实质是功,而且是假想的单位力在真实的位移上所做的虚功。由此看来,我们利用虚功解 决了直接利用功能原理不便计算位移的困难。 若需要计算某一截面的转角,则在需要计算转角的截面及转动方向上假想地加一个单位 力偶矩,用与上面类似的方法,得到计算转角的莫尔积分 0=MM达 E (13-11) 式中M(x)是给定载荷作用下的弯矩,”(x)是单位力偶矩作用下的弯矩。 对于组合变形杆,莫尔积分可表示为 5=NN但+4M.但+jM.(eM田h (13-12) EI. 式中8为广义位移(线位移或角位移),N(x)、M(x)、M(x)为给定载荷作用下的轴力、弯 矩、扭矩,(x)、(x)、M。(x)为广义单位力(力或力偶矩)作用下的内力。对于圆截面 杆,式中I为极惯性矩,对于非圆成面杆,应将I换成相当的几何量。 桁架的每根杆均为轴向拉伸或压缩杆,且为二力杆(每杆中轴力为常数),设有根杆 则架的莫尔定理可写成 5->NN EA (13-11) 将莫尔定理推广到小曲率曲杆,则对应于(1312)式中的x应改为现长S。例如,若仅 考虑弯曲变形能,则 &=Ms包 (13-14) E7, 例13-2简支梁跨中受集中力P作用(图a),求B支座截面的转角8,设E1:已知. 241 This document is generated by trial version of Print2Flash(www.printflash.com)
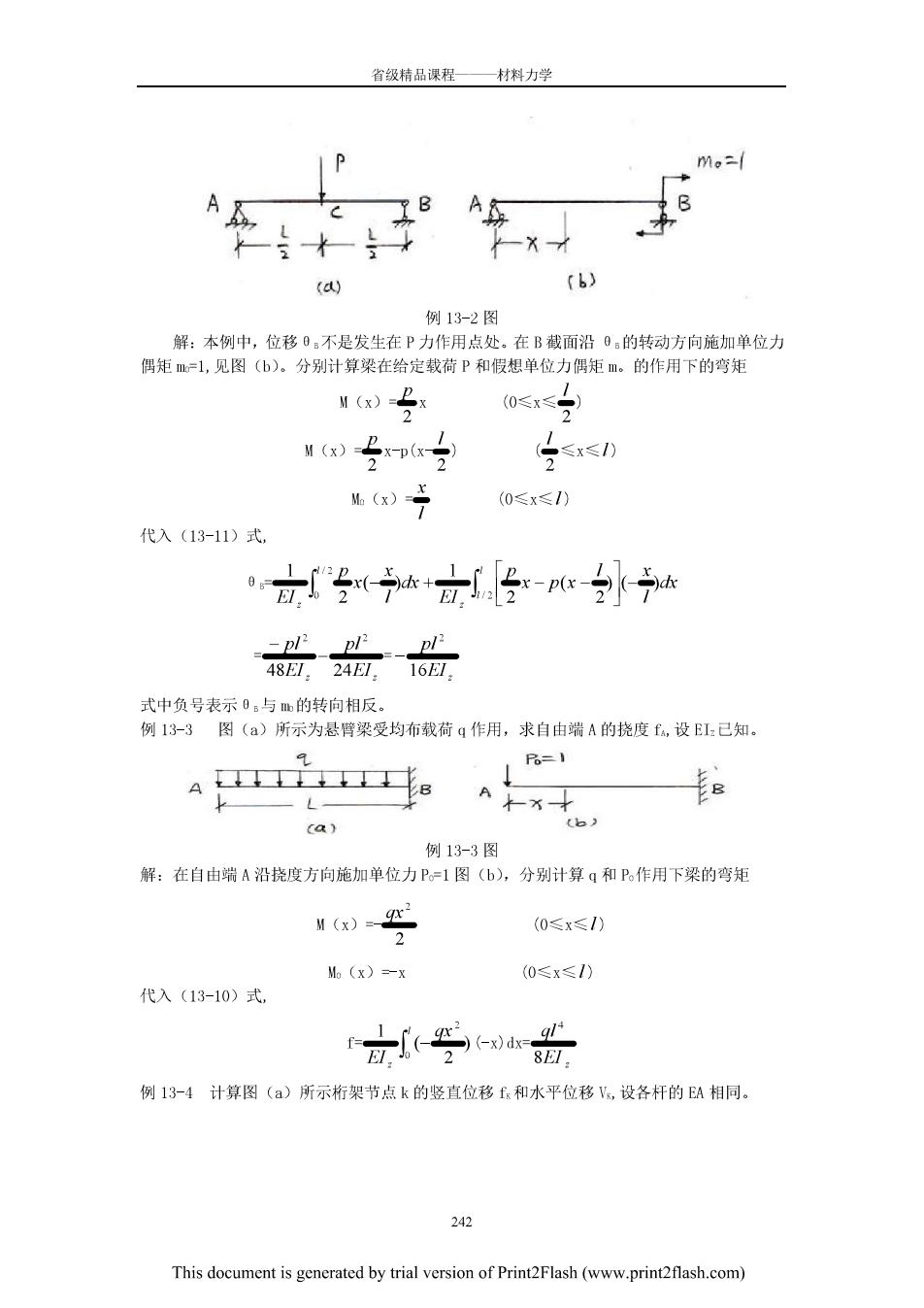
省级精品课程—材料力学 A TB A 一X () (b) 例13-2图 解:本例中,位移9:不是发生在P力作用点处。在B截面沿0:的转动方向施加单位力 偶矩皿=1,见图(b)。分别计算染在给定载荷P和假想单位力偶矩m。的作用下的弯矩 M(x)=巳x (0≤x≤号) M(x)号xpx 是(x)于 (0≤x≤I) 代入(13-11)式 0(7+经-p27 -p/2p/2 D/ 48EL,24EL,-16E, 式中负号表示。与m的转向相反 例13-3图(a)所示为悬臂梁受均布载荷q作用,求自由端A的挠度f,设EI:已知。 8 9 人, ca) 例13-3图 解:在自由端A沿挠度方向施加单位力P。=1图(b),分别计算q和P,作用下梁的弯矩 (0≤x≤1) (x)=一X (0≤x≤) 代入(13-10)式. 立f罗w品 例13-4计算图()所示析架节点k的竖直位移和水平位移,设各杆的A相同。 242 This document is gencrated by trial version of Print2Flash(www.printflash.com)
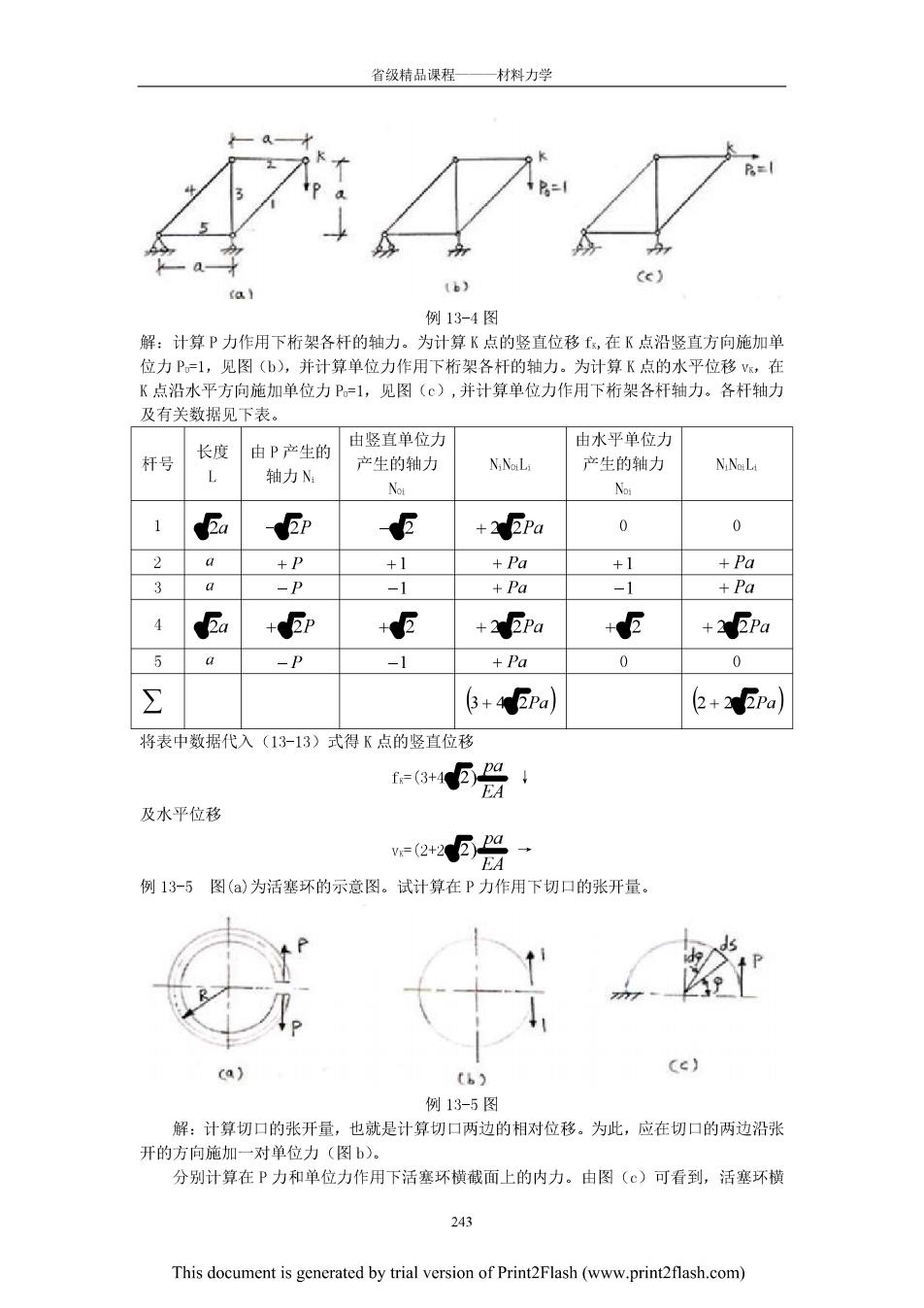
省领精品课程一材料力学 I6) 例13-4图 解:计算P力作用下桁架各杆的轴力。为计算K点的竖直位移,在K点沿竖直方向施加单 位力P=1,见图(b),并计算单位力作用下桁架各杆的轴力。为计算K点的水平位移,在 K点沿水平方向施加单位力P。=1,见图(),并计算单位力作用下桁架各杆轴力。各杆轴力 及有关数据见下表。 由区古单位力 杆号 长度 由P产生的 由水平单位力 产生的轴力 NiNaLa 严生的轴力 轴力N: N.NaL Nat Not 1 E 2 +2EPo 0 0 2 +卫 +P% +1 +Pa 30 -1 +Pa -1 +Pa 4 + r2 +22Po +E +22Pa -P -1 +Pa 0 0 (3+4pa) e+Era) 将表中数据代入(13-13)式得K点的竖直位移 e8F侣: 及水平位移 -2+2E兴 例13-5图()为活塞环的示意图。试计算在P力作用下切口的张开量。 ca) Ce) t55 12-5 解:计算切口的张开量,也就是计算切口两边的相对位移。为此,应在切口的两边沿张 开的方向施加一对单位力(图b). 分别计算在P力和单位力作用下活塞环横截面上的内力。由图(c)可看到,活塞环横 24g3 This document is generated by trial version of Print2Flash(www.printflash.com)

省领精品课程—材料力学 被面上的内力一般有轴力、剪力和弯矩,因此活塞环产生组合变形。略去剪切变形,仅考虑 弯曲和拉压变形,相应的内力是 (p)=-PR(I-cosp) (p)=-Pcosp M (p)=-R(1-cosp) N。(p)=-cosp 这里,规定使曲杆的曲率增加时弯矩取正号,反之为负。利用公式(13-14)并注意组合变 形,以及活塞环的对称性,得 624sY.@2NoN@k EA 子IMoM,(oup子IoN,oRe 置-plo+设osa 为比较上式中的两项,暂且按直径为d的圆截面,且=5d估计,由此得到 6=(2400+20)a 可见,第二项可略去不计,切口的张开量主要由弯曲变形而引起 §13.3图乘法 在对染和刚架应用莫尔定理时,要计算积分 [MMs达 El. 对于等直杆,EI为常数,故上面积分变为 [M(x)M,(x)dx 在单位力或单位力偶矩的作用下,直杆的贴(x)图必定是直线或折线,这个特点使我 们可以利用弯矩图较方便地完成积分(a)。 244 This document is generated by trial version of Print2Flash(www.print2flash.com)