
Theorem(Sum Principle) SnT=0→ISUT=S1+T到 4口·¥①,4三,t更,3)Q0 Jun Ma (majunainju.edu.cn) 2-3 Counting March 9.2022 9/35
Theorem (Sum Principle) S ∩ T = ∅ =⇒ |S ∪ T| = |S| + |T| Theorem (Product Principle) |S × T| = |S| × |T| Holds for finite sets S and T. Jun Ma (majun@nju.edu.cn) 2-3 Counting March 9, 2022 9 / 35

Theorem(Sum Principle) SnT=0→ISUT川=lS1+lT Theorem (Product Principle) IS×T=IS×T 4口·¥①,43,t夏,里Q0 Jun Ma (majunainju.edu.cn) 2-3 Counting March 9.2022 9/35
Theorem (Sum Principle) S ∩ T = ∅ =⇒ |S ∪ T| = |S| + |T| Theorem (Product Principle) |S × T| = |S| × |T| Holds for finite sets S and T. Jun Ma (majun@nju.edu.cn) 2-3 Counting March 9, 2022 9 / 35

Theorem(Sum Principle) SnT=0→ISUT=S1+1T Theorem (Product Principle) IS×T=IS×T Holds for finite sets S and T. 4口·¥①,4三,t更,里)Q0 Jun Ma (majunainju.edu.cn) 2-3 Counting March 9.2022 9/35
Theorem (Sum Principle) S ∩ T = ∅ =⇒ |S ∪ T| = |S| + |T| Theorem (Product Principle) |S × T| = |S| × |T| Holds for finite sets S and T. Jun Ma (majun@nju.edu.cn) 2-3 Counting March 9, 2022 9 / 35
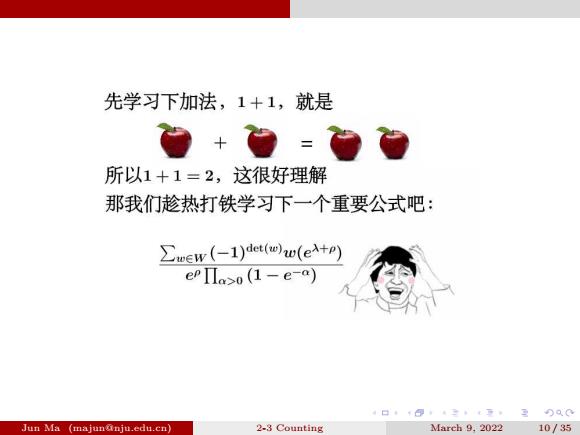
先学习下加法,1+1,就是 +- 所以1+1=2,这很好理解 那我们趁热打铁学习下一个重要公式吧: EwEw(-1)det(w)w(ex+) ePΠa>o(1-e-a) 4口·1①,43,t夏,3)Q0 Jun Ma (majunainju.edu.cn) 2-3 Counting March 9.2022 10/35
Jun Ma (majun@nju.edu.cn) 2-3 Counting March 9, 2022 10 / 35
Counting 4口·¥①,4三,t更,3)Q0 Jun Ma (majunainju.edu.cn) 2-3 Counting March 9.2022 11/35
tuples permutations combinations Counting compositions set partitions integer partitions Counting # of functions under (twelve) different restrictions Jun Ma (majun@nju.edu.cn) 2-3 Counting March 9, 2022 11 / 35