
Optimal Determination of Source-destination Connectivity in Random Graphs Luoyi Fu,Xinbing Wang,P.R.Kumar Dept.of Electronic Engineering Shanghai Jiao Tong University Dept.of Electrical Computer Engineering Texas A&M University
Optimal Determination of Source-destination Connectivity in Random Graphs Luoyi Fu, Xinbing Wang, P. R. Kumar Dept. of Electronic Engineering Shanghai Jiao Tong University Dept. of Electrical & Computer Engineering Texas A&M University
Random Graph:G(n,p)Model ●N nodes ● Each edge exists with probability p Proposed by Gilbert in 1959 ● Called ER graph 2/19
Random Graph: G(n,p) Model ⚫ N nodes ⚫ Each edge exists with probability p ⚫ Proposed by Gilbert in 1959 ⚫ Called ER graph 2/19
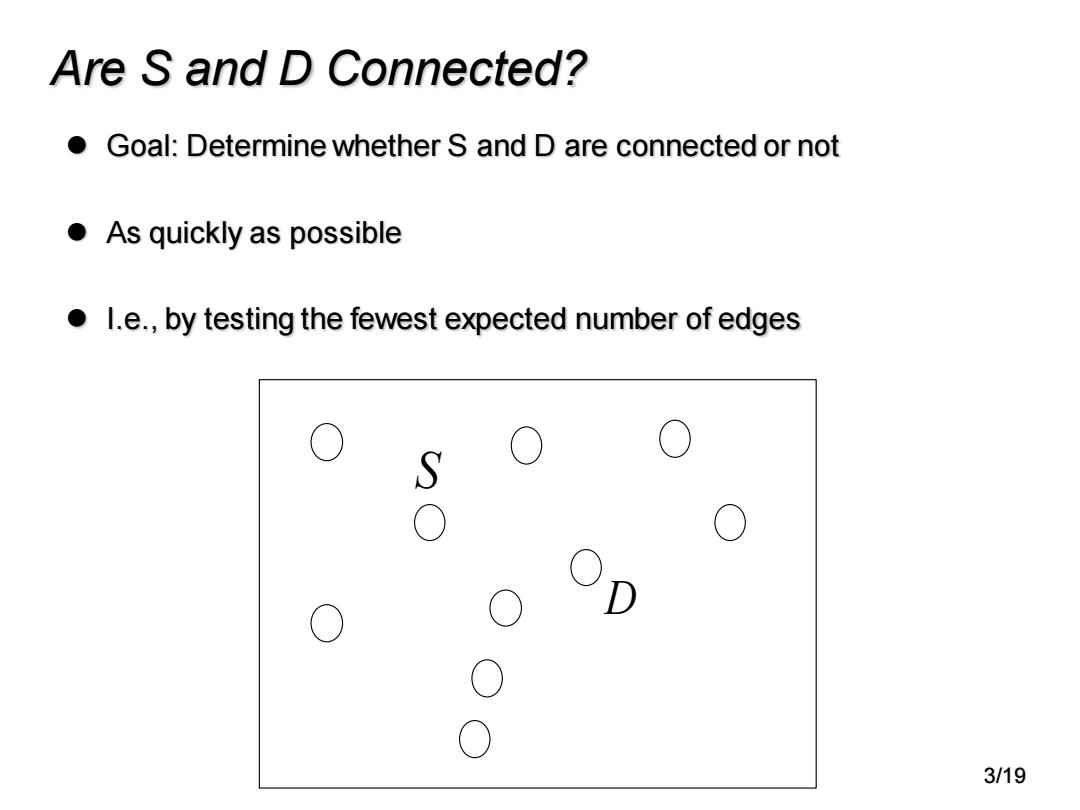
Are S and D Connected? o Goal:Determine whether S and D are connected or not ●As quickly as possible l.e.,by testing the fewest expected number of edges S O 0 D O 0 ○ 0 3/19
Are S and D Connected? ⚫ Goal: Determine whether S and D are connected or not ⚫ As quickly as possible ⚫ I.e., by testing the fewest expected number of edges S D 3/19
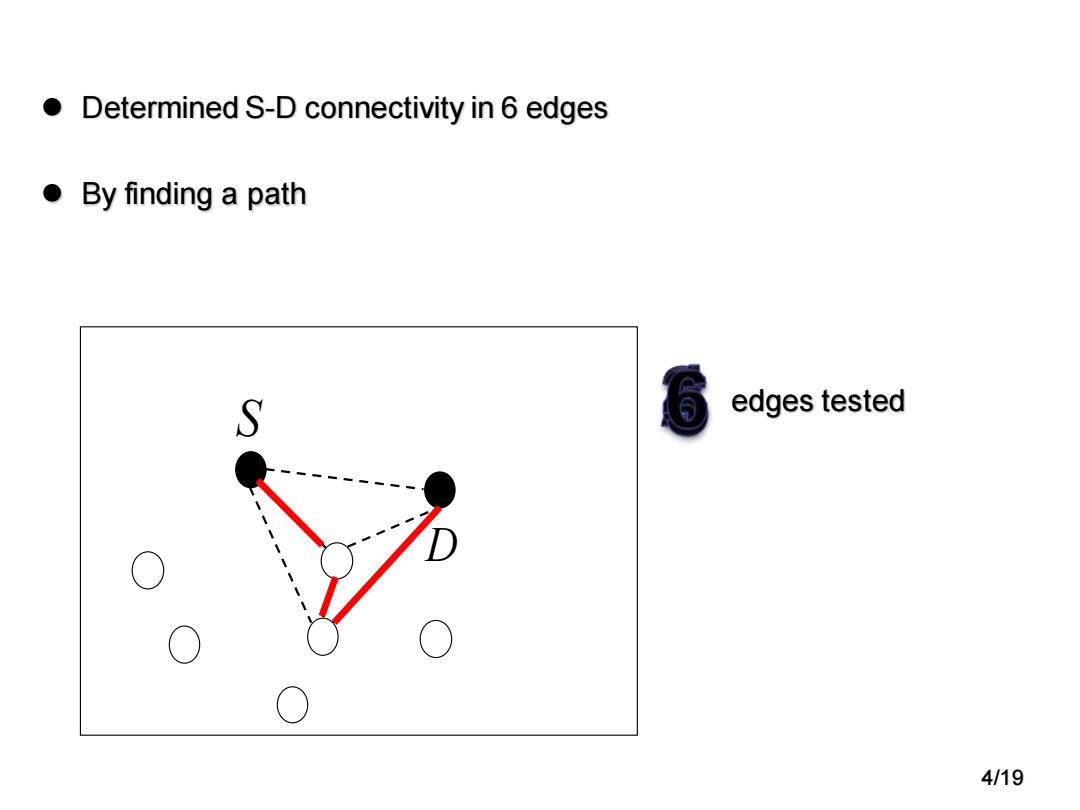
● Determined S-D connectivity in 6 edges ●By finding a path S edges tested O 4/19
⚫ Determined S-D connectivity in 6 edges ⚫ By finding a path S D edges tested 4/19
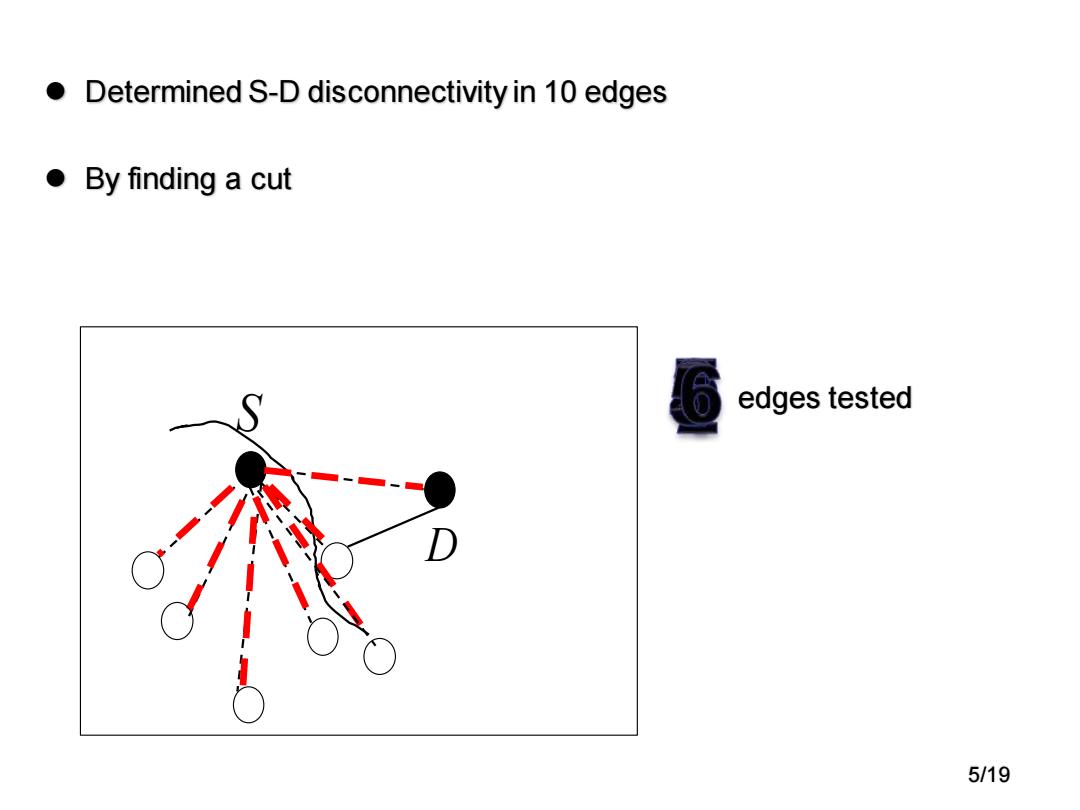
● Determined S-D disconnectivity in 10 edges ●By finding a cut 6 edges tested 5/19
⚫ Determined S-D disconnectivity in 10 edges ⚫ By finding a cut S D edges tested 5/19