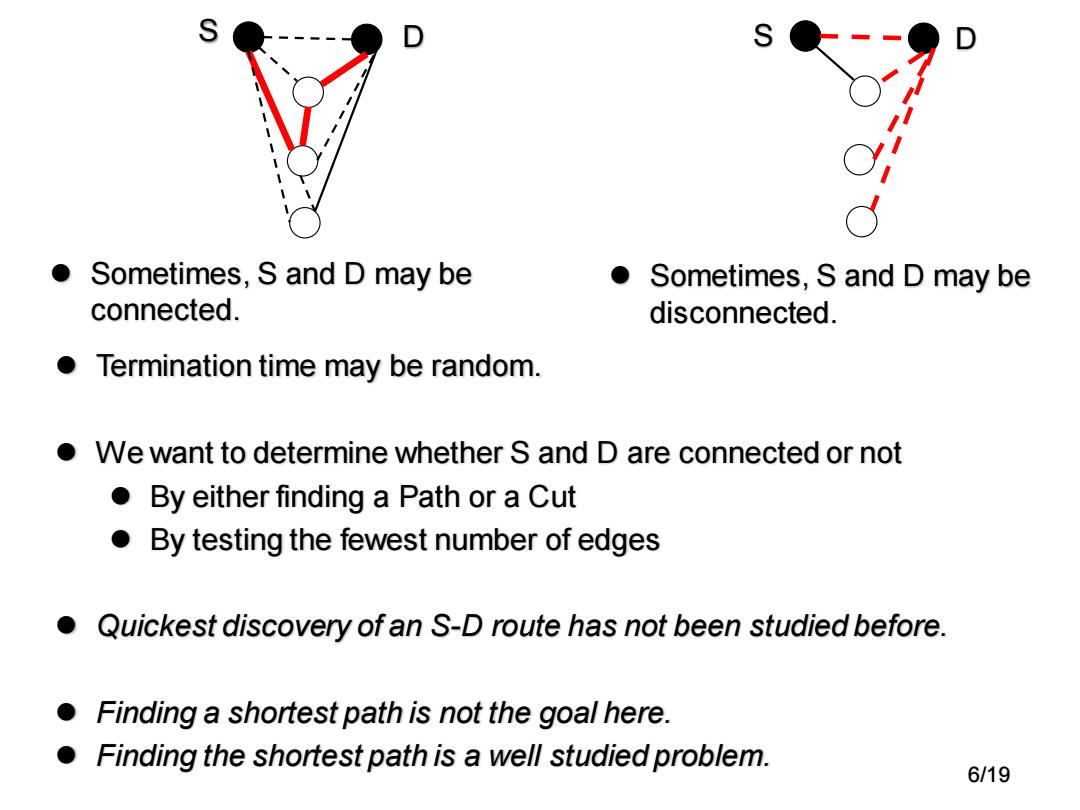
Sometimes,S and D may be ● Sometimes,S and D may be connected. disconnected. Termination time may be random. o We want to determine whether S and D are connected or not By either finding a Path or a Cut o By testing the fewest number of edges ● Quickest discovery of an S-D route has not been studied before. Finding a shortest path is not the goal here. Finding the shortest path is a well studied problem. 6/19
S D S D ⚫ Termination time may be random. ⚫ We want to determine whether S and D are connected or not ⚫ By either finding a Path or a Cut ⚫ By testing the fewest number of edges ⚫ Quickest discovery of an S-D route has not been studied before. ⚫ Finding a shortest path is not the goal here. ⚫ Finding the shortest path is a well studied problem. 6/19 ⚫ Sometimes, S and D may be connected. ⚫ Sometimes, S and D may be disconnected
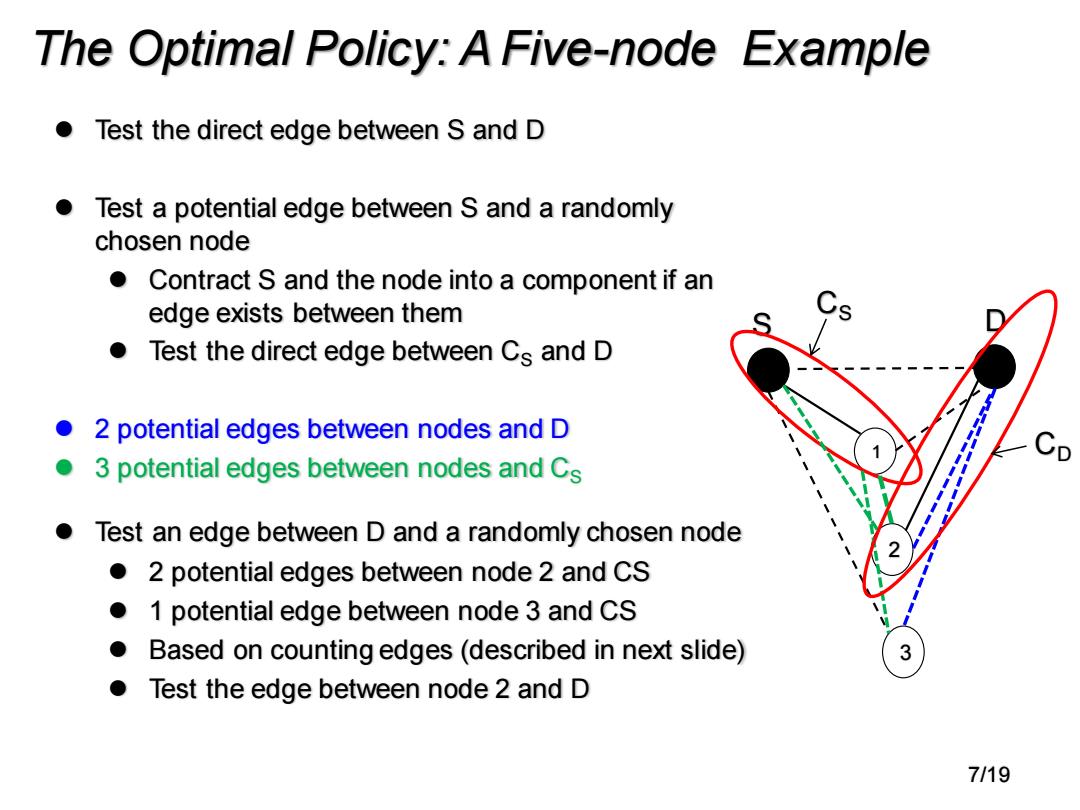
The Optimal Policy:A Five-node Example Test the direct edge between S and D Test a potential edge between S and a randomly chosen node ● Contract S and the node into a component if an edge exists between them Test the direct edge between Cs and D 2 potential edges between nodes and D 0 3 potential edges between nodes and Cs Test an edge between D and a randomly chosen node 2 potential edges between node 2 and CS ● 1 potential edge between node 3 and CS ● Based on counting edges(described in next slide) 3 Test the edge between node 2 and D 7/19
⚫ Test the direct edge between S and D ⚫ Test a potential edge between S and a randomly chosen node ⚫ Contract S and the node into a component if an edge exists between them ⚫ Test the direct edge between CS and D ⚫ 2 potential edges between nodes and D ⚫ 3 potential edges between nodes and CS ⚫ Test an edge between D and a randomly chosen node ⚫ 2 potential edges between node 2 and CS ⚫ 1 potential edge between node 3 and CS ⚫ Based on counting edges (described in next slide) ⚫ Test the edge between node 2 and D The Optimal Policy: A Five-node Example 1 3 2 S D CS CD 7/19