
Outline (Level 1-2) Preparatory knowledge o Linear Activation Function o Threshold Activation Function S-Shaped Activation Function 10/77
Outline (Level 1-2) 2 Preparatory knowledge Linear Activation Function Threshold Activation Function S-Shaped Activation Function 10 / 77
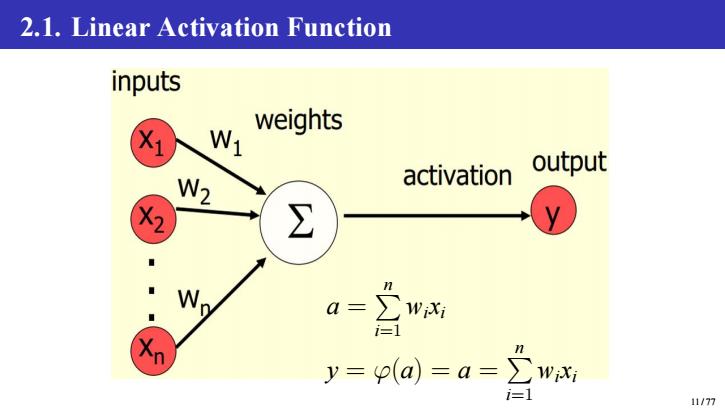
2.1.Linear Activation Function inputs N weights activation output W2 ∑ W a= WiXi i=1 n y=p(a=a=∑ WiXi i=1 11/77
2.1. Linear Activation Function a = P n i=1 wixi y = φ(a) = a = P n i=1 wixi 11 / 77

Gradient descent learning rule oWe examine linear neurons(without thresholds and continuous output y(not discrete values such as-1 and 1). ●y=W0+1W1x1+.+1wmxn Training weight w;to make the following functions minimum. Eo,w-,wl=2∑u-%P dE∈D where,D is training dataset,(xd,ta)ED 12/77
Gradient descent learning rule We examine linear neurons (without thresholds and continuous output y (not discrete values such as -1 and 1). y = w0 + w1x1 + ... + wnxn Training weight wi to make the following functions minimum. E[w0,w1, ..., wn] = 1 2 X d∈D (td − yd) 2 where, D is training dataset, (xd, td) ∈ D 12 / 77
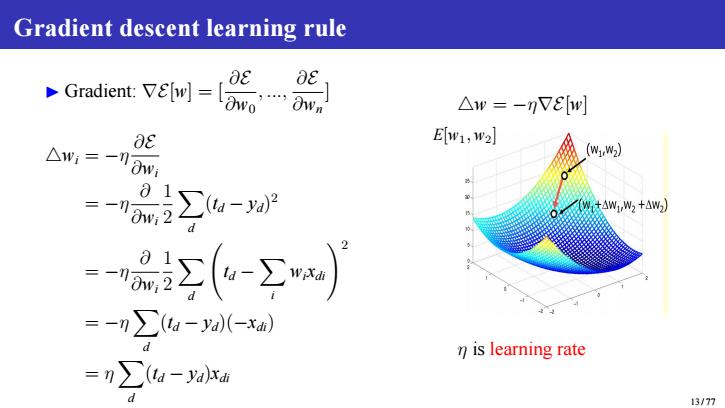
Gradient descent learning rule Gradient:w △w=-VEbw] aE E[w1,w2] △w:=一n0w (w1w2) 三一01 5∑a-aP W达△W1,W2+△W) d -∑(6-∑ =-n∑a-a(-xah) n is learning rate =n∑a-yaxa 13/77
Gradient descent learning rule ▶ Gradient: ∇E[w] = [ ∂E ∂w0 , ..., ∂ E ∂ w n ] △ w i = − η ∂ E ∂ w i = − η ∂∂w i 12 Xd ( td − y d ) 2 = − η ∂∂w i 12 Xd td − Xi w i xdi ! 2 = − η Xd ( td − y d)( − xdi ) = η Xd ( td − y d ) xdi △ w = − η∇E [ w ] E [ w 1 , w 2 ] η is learning rate 13 / 77

Stochastic gradient descent (SGD)algorithm o Batch Learning: w'w-nVED[w] Update using the entire dataset D,object function is: olw]=1/2a-a)2 Stochastic Gradient Descent(SGD) w'=w-nVEdlw] Update using single sample d,object function is: Edlw]1/2(ta-ya) If the learning rate n is small enough,the SGD algorithm can approach the batch learning method. 14/77
Stochastic gradient descent (SGD) algorithm Batch Learning: w ′ = w − η∇ED[w] Update using the entire dataset D, object function is: ED[w] = 1/2X d (td − yd) 2 Stochastic Gradient Descent (SGD) w ′ = w − η∇Ed[w] Update using single sample d, object function is: Ed[w] = 1/2(td − yd) 2 If the learning rate η is small enough, the SGD algorithm can approach the batch learning method. 14 / 77