
Outline (Level 1) History Preparatory knowledge XOR problem MLP is doing what? Tilling Algorithm Learning algorithm for MLP of differentiable activation function 5/77
Outline (Level 1) 1 History 2 Preparatory knowledge 3 XOR problem 4 MLP is doing what? 5 Tilling Algorithm 6 Learning algorithm for MLP of differentiable activation function 5 / 77
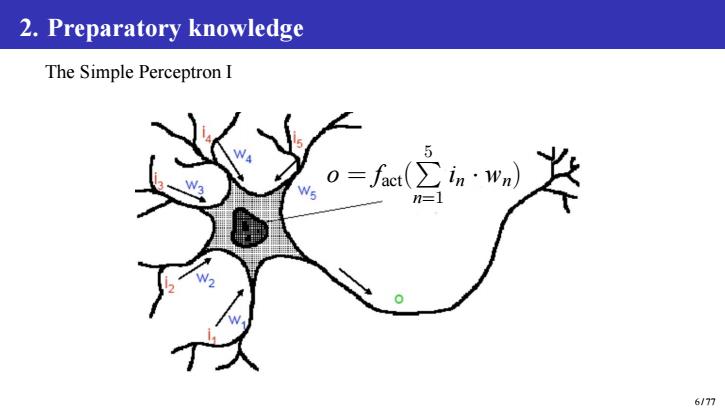
2.Preparatory knowledge The Simple Perceptron I 5 n=1 6/77
2. Preparatory knowledge The Simple Perceptron I o = fact( P 5 n=1 in · wn) 6 / 77
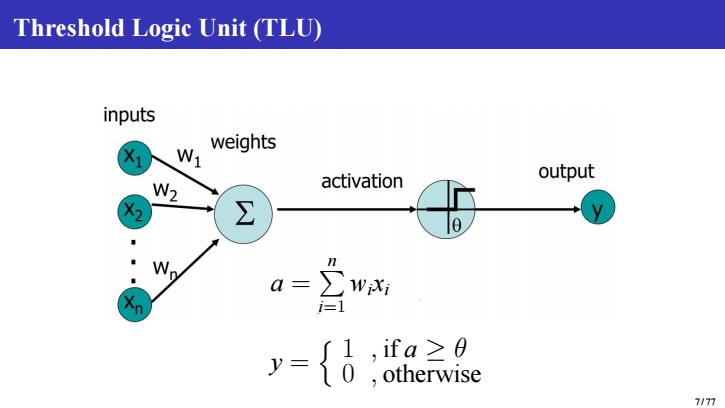
Threshold Logic Unit (TLU) inputs X1 N weights activation output W2 X ∑ o n a= WiXi y= {0 ,ifa≥0 otherwise 7/77
Threshold Logic Unit (TLU) a = P n i=1 wixi y = n 1 , if a ≥ θ 0 , otherwise 7 / 77
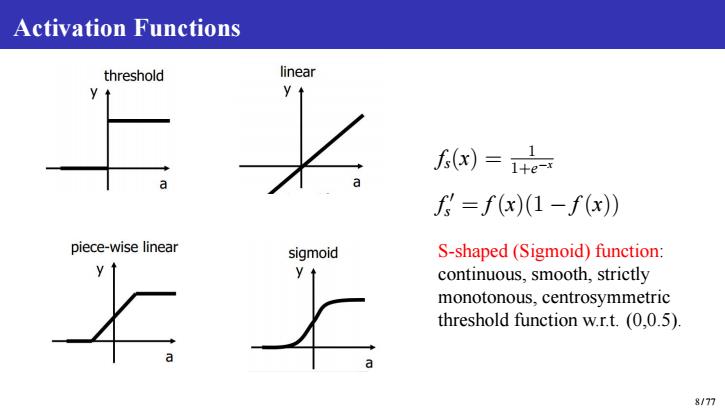
Activation Functions threshold linear )=+ =f(x)(1-f(x)) piece-wise linear sigmoid S-shaped(Sigmoid)function: continuous,smooth,strictly monotonous,centrosymmetric threshold function w.r.t.(0,0.5). 8/77
Activation Functions fs(x) = 1 1+e−x f ′ s = f (x)(1 − f (x)) S-shaped (Sigmoid) function: continuous, smooth, strictly monotonous, centrosymmetric threshold function w.r.t. (0,0.5). 8 / 77

Sigmoidal Functions Logistic function: Increasing a p(y)=1+e-y where 108642246810 ∑ WjiXi i=1 v is the induced field of neuron j oSigmoidal functions is the general form of activation function ●a→o→p→threshold function Sigmoidal functions is differentiable 9177
Sigmoidal Functions Logistic function: φ(vj) = 1 1 + e −avj where vj = Xm i=1 wjixi vj is the induced field of neuron j Sigmoidal functions is the general form of activation function a → ∞ ⇒ φ → threshold function Sigmoidal functions is differentiable 9 / 77