2-7将质量为10kg的小球挂在倾角 a=30的光滑斜面上(如图)。 (1)当斜面以加速度g/3沿如图所示的 方向运动时,求绳中的张力及小球对斜面的 正压力。 (2)当斜面的加速度至少为多大时,小 球对斜面的正压力为零? 结束目录
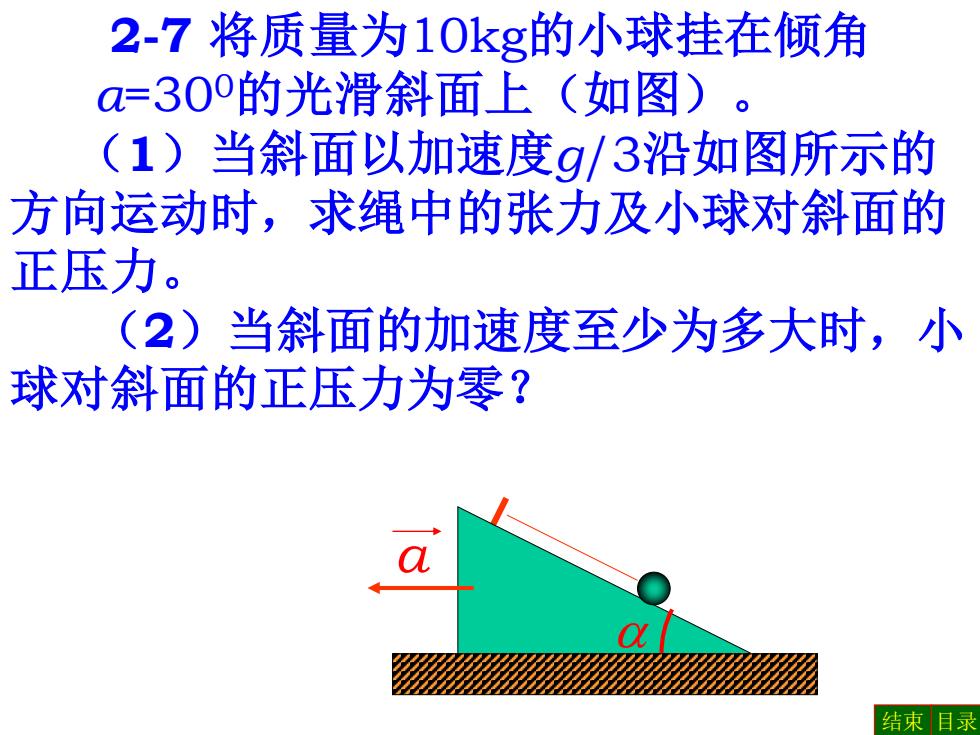
2-7 将质量为10kg的小球挂在倾角 α=300的光滑斜面上(如图)。 (1)当斜面以加速度g/3沿如图所示的 方向运动时,求绳中的张力及小球对斜面的 正压力。 (2)当斜面的加速度至少为多大时,小 球对斜面的正压力为零? a a 结束 目录

已知:, m=10kg0=300 N 求:(1)a=3g时TN (2)a=?时N=0 mg 解:(1)Tcosa-Vsina=ma Tsin a+Ncosa-mg=0 T=mgsina+ma cosa mg (sinat 3 cosa)=77.3N N=mgcosa-masin a mg(cosa-asin a =68.4N 结束目录
已知: m=10kg a =300 1 3 求:(1) a = g 时 T N (2) a =? 时 N=0 a a T N mg Tsin a +Ncosa mg = 0 T = mgsina +ma cosa N = mgcosa masin a 解:(1) Tcosa Nsina = ma ( ) 1 3 = mg sina + cosa = mg cosa sin a 1 3 ( ) = 77.3N = 68.4N 结束 目录

(2)当N=0 Tcosa=ma Tsin a-mg =0 g tga= a a-tga=17m/s2 结束目录
Tsin a mg = 0 Tcosa = ma (2) 当 N=0 a a g tg = a a g tg = =17m/s2 结束 目录

2-8摩托快艇以速率。行驶,它受到的 摩擦阻力与速度平方成正比,设比例系数为 常数飞,则可表示为F=-kP.设摩托快艇的 质量为m,当摩托快艇发动机关闭后, (1)求速度v对时间的变化规律。 (2)求路程x对时间的变化规律。 (3)证明速度v与路程x之间有如下关系: v=voex(式中的k'=k/m。) (4)如果。=20m/s,经15s后,速度降为 v10m/s,求k'。 (5)画出x、vU、a随时间变化的图形。 结束目录
2-8 摩托快艇以速率 v0行驶,它受到的 摩擦阻力与速度平方成正比 ,设比例系数为 常数k,则可表示为 F = -k v2.设摩托快艇的 质量为m,当摩托快艇发动机关闭后, (1)求速度v对时间的变化规律。 (2)求路程x对时间的变化规律。 (3)证明速度v与路程x之间有如下关系: v = v0e -k’x (式中的 k’ =k/m。) (4)如果v0=20m/s,经15s后,速度降为 vt=10m/s, 求k’ 。 (5)画出x、v、a随时间变化的图形。 结束 目录

已知:V。F=-kv2m 求:(1)v(t)(2)x(t)(3)证明v=voe-kx 解:(1)F=-kU2=m dv dt dv=-k'v2 d k'=飞 dv m 02=-'dt kdt 1-1=k't ● Vo )= 1+vok t 结束目录
已知:v0 F= kv 2 m 求:(1)v ( t ) (2)x ( t ) (3)证明v = v0e -k’x 解:(1) d d v t F k 2 = v =m k´ = k m ∵ = d d v t k 2 ´ v = ´ d d v k t v 2 = ´ d d v k t v 2 v t v0 0 = v 0 t 1 v 1 k´ v = 0 1 +v k´t v0 ∴ 结束 目录