
Bias(x)=Ep(x)-p()= Pi -p() h =p@h+h✉hG-1/2)--p( h =p(x)[h(0-1/2)-x. BiasP(ced-(()-12)d 》得

V(x)= nh2 p(r)h+hp'(x)[h(j-1/2)-x] nh2 ≈p(r)/nh. R(m,p)≈ 极小化上式,得到理想带宽为 1/3 h=Cn-1/3
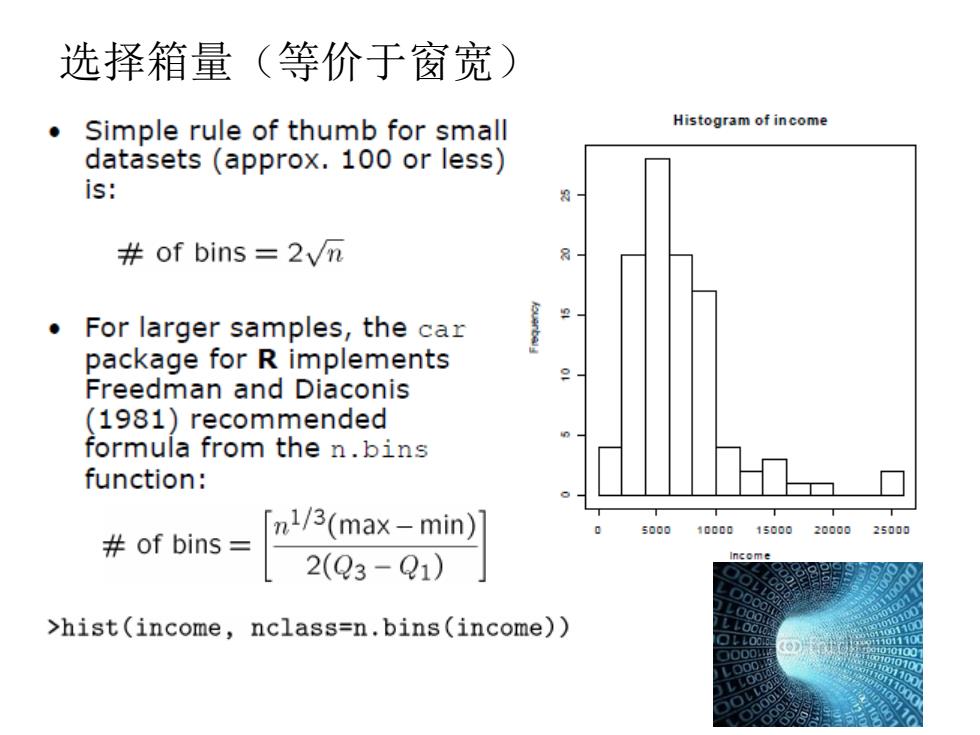
选择箱量(等价于窗宽) Simple rule of thumb for small Histogram of income datasets(approx.100 or less) is: of bins =2vn For larger samples,the car package for R implements Freedman and Diaconis (1981)recommended formula from the n.bins function: 5000 10000150002000025000 #of bins= n3(max-tw 2(Q3-Q1) >hist(income,nclass=n.bins(income))
选择箱量(等价于窗宽)

偏差与方差分解 Choice of hypothesis class introduces learning bias ▣More complex class→less bias More complex class-more variance 模型偏差太大 模型方差太大
偏差与方差分解 模型偏差太大 模型方差太大

bias-variance偏差和方差分解 For any estimator MSE(0)=E(0-0)2 =E(0-E(0)+E(0)-0)2 =E(0-E(0)2+E(E(0)-0)2 =Var(0)+(E(0)-0)2 bias Note MSE closely related to prediction error: E(Yo-xB)2=E(Yo-xB)2+E(xB-xB)2=2+MSE(xB)
bias-variance偏差和方差分解 ~ 2 2 2 2 ) ) ~ ) ( ( ~ ( ) ) ~ )) ( ( ~ ( ~ ( ) ) ~ ) ( ~ ( ~ ( = + − = − + − = − + − Var E E E E E E E E 2 ) ~ ) ( ~ MSE( = E − For any estimator : bias Note MSE closely related to prediction error: ) ~ ) ( ~ ) ( ) ( ~ ( 0 2 2 0 0 2 0 0 2 0 0 T T T T T E Y − x = E Y − x + E x − x = + MSE x