中国科学技术大学：《应用回归分析》课程教学资源（课件讲义）第三章 多元线性回归

第三章多元线性回归 3.1多元线性回归模型 3.2回归参数的估计 3.3参数估计量的性质 3.4回归方程的显著性检验 3.5中心化和标准化 3.6相关阵与偏相关系数 3.7本章小结与评注

第三章 多元线性回归 3.1 多元线性回归模型 3.2 回归参数的估计 3.3 参数估计量的性质 3.4 回归方程的显著性检验 3.5 中心化和标准化 3.6 相关阵与偏相关系数 3.7 本章小结与评注

3.1多元线性回归模型 一、多元线性回归模型的一般形式 Bo+Bx+B2x2+...+Bpxp+8 E(8)=0 var(g)=o2

3.1 多元线性回归模型 一、多元线性回归模型的一般形式 y=β0+β1 x1+β2 x2+…+βp xp+ε      2 var( ) ( ) 0   E 

3.1多元线性回归模型 一、多元线性回归模型的一般形式 对组观测数据(x1,x2,…xpy,泸1,2，，n, 线性回归模型表示为： y=Bo+Bx+B2x12++Bpxip+ y2=B。+Bx21+B2x22++Bpx2p+82 yn =Bo+Bxm+B2xn2++Bpxmp+En

3.1 多元线性回归模型 一、多元线性回归模型的一般形式 对n组观测数据 (xi1 , xi2 ,…,xip; yi ), i=1,2,…,n, 线性回归模型表示为:                          n n n p np n p p p p y x x x y x x x y x x x                    0 1 1 2 2 2 0 1 21 2 22 2 2 1 0 1 11 2 12 1 1

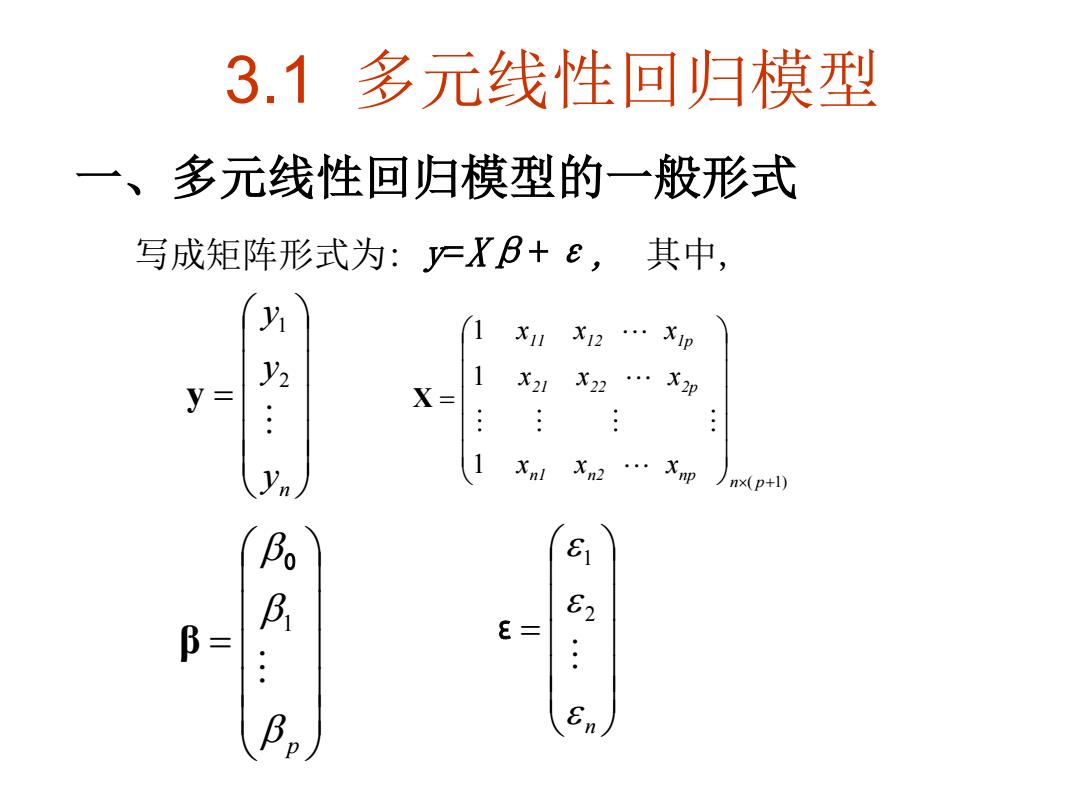
3.1多元线性回归模型 一、多元线性回归模型的一般形式 写成矩阵形式为：=XB+e,其中， 1x1x2…xp y2 1 y= X= X21 x22…X2p yn 1 nlXn2…Xpnp+D B B 82 B= E= En

3.1 多元线性回归模型 一、多元线性回归模型的一般形式 写成矩阵形式为: y=Xβ+ε, 其中,                n y y y  2 1 y ( 1) 1 1 1                  n p n1 n2 np 21 22 2p 11 12 1p x x x x x x x x x        X                 p    1 0 β                n     2 1 ε

3.1多元线性回归模型 二、多元线性回归模型的基本假定 1.解释变量x12,…x,是确定性变量，不是随机变量， 且要求rk(X)=pt1<n。 表明设计矩阵X中的自变量列之间不相关， X是一满秩矩阵

3.1 多元线性回归模型 二、多元线性回归模型的基本假定 1. 解释变量x1 ,x2 ,…,xp是确定性变量,不是随机变量, 且要求rk(X)=p+1＜n。 表明设计矩阵X中的自变量列之间不相关, X是一满秩矩阵