《工程塑性理论》课程授课教案（讲义，共九讲）

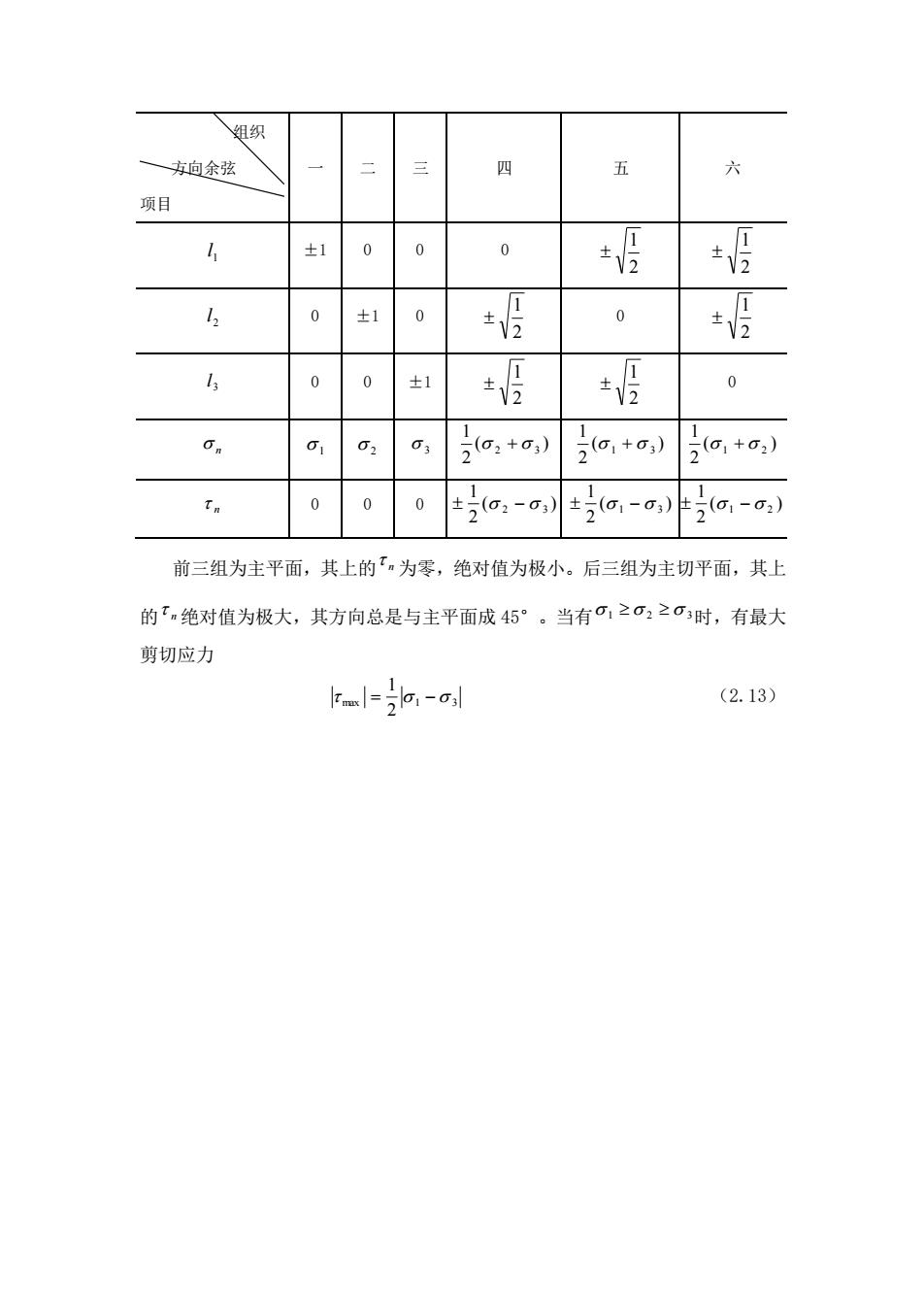
组织 一东向余弦 项目 1 0 0 0 报 0 1 0 ±阳 0 ±1 ±报 0 5(o2+0) (1+0) a,+:) T. 0 0 0 +(G:-G (a-a,) 前三组为主平面，其上的'：为零，绝对值为极小。后三组为主切平面，其上 的7绝对值为极大，其方向总是与主平面成45°。当有000时，有最大 剪切应力 lml-jl,-al (2.13)

组织 方向余弦 项目 一 二 三 四 五 六 1 l ±1 0 0 0 2 1  2 1  2 l 0 ±1 0 2 1  0 2 1  3 l 0 0 ±1 2 1  2 1  0  n  1  2  3 ( ) 2 1  2 +  3 ( ) 2 1  1 +  3 ( ) 2 1  1 +  2 n  0 0 0 ( ) 2 1   2 − 3 ( ) 2 1   1 − 3 ( ) 2 1   1 − 2 前三组为主平面，其上的 n  为零，绝对值为极小。后三组为主切平面，其上 的 n  绝对值为极大，其方向总是与主平面成 45°。当有  1  2  3 时，有最大 剪切应力 max 1 3 2 1  =  − （2.13）

第二讲工程塑性理论 教学内容： 本章讨论了应力球张量与应力偏张量，八面体应力与等效应力，应力分析和 应变分析是塑性变形的力学基础， 教学重点： 应力球张量与应力偏张量，八面体应力与等效应力 教学难点： 应力球张量与应力偏张量，八面体应力与等效应力 教学方法： 课堂教学为主，结合多媒体教学。 教学要求： 应力球张量与应力偏张量，八面体应力与等效应力 教学时间： 应力球张量与应力偏张量50min:八面体应力与等效应力50min: 1.2.4应力球张量与应力偏张量 塑性变形时体积变化为零，只有形状变化。因此，可以把‘分解成与体积变 化有关的量和与形状有关的量。前者称应力球张量，后者称应力偏张量。设·为 平均应力，则有： 0.=o+0,+a)= (2.14) 按照应力叠加原理，“：具有可分解性。因此有： Gy=(Gy-G8)+Gm6 =oy+o0(6,j=x,y,) (2.15) 式中，当=j时，0，=1，当≠j时，0，=0。 上式第一项为应力偏张量，其主轴方向与原应力张量相同。第二项为应力球 张量，其任何方向都是主方向，且主应力相同

第二讲 工程塑性理论 教学内容： 本章讨论了应力球张量与应力偏张量，八面体应力与等效应力，应力分析和 应变分析是塑性变形的力学基础。 教学重点： 应力球张量与应力偏张量，八面体应力与等效应力 教学难点： 应力球张量与应力偏张量，八面体应力与等效应力 教学方法： 课堂教学为主，结合多媒体教学。 教学要求： 应力球张量与应力偏张量，八面体应力与等效应力 教学时间： 应力球张量与应力偏张量 50min；八面体应力与等效应力 50min； 1.2.4 应力球张量与应力偏张量 塑性变形时体积变化为零，只有形状变化。因此，可以把  ij 分解成与体积变 化有关的量和与形状有关的量。前者称应力球张量，后者称应力偏张量。设  m 为 平均应力，则有： 1 3 1 ( ) 3 1 I  m =  x +  y +  z = （2.14） 按照应力叠加原理，  ij 具有可分解性。因此有：  ij =  ij − m ij + m ij ( ) ' (i, j x, y,z) = ij + m ij = （2.15） 式中，当 i = j 时，  ij = 1 ；当 i  j 时，  ij = 0 。 上式第一项为应力偏张量，其主轴方向与原应力张量相同。第二项为应力球 张量，其任何方向都是主方向，且主应力相同

值得一提的是，·可，只影响体积变化，不影响形状变化，但它关系到材料 塑性的充分发挥。三向压应力有利于材料塑性的发挥。 应力偏张量仍然是一个二阶对称张量，同样有三个不变量，分别为 ,2,3 1=c+o',+o=0 2=a,-o,+o,-a尸+(a-o,)+6号+r片+r (2.16) r3=G'u ,=0表明应力偏张量己不含平均应力成份。？与屈服准则有关（见第二 章)，反映了物体形状变化的程度。·反映了变形的类型：·>0表示广义拉伸 变形：I3=0表示广义剪切变形，1<0表示广义压缩变形。 1.2.5八面体应力与等效应力 在主应力空间中，每一掛限中均有一组与三个坐标轴成等倾角的平面，八个 掛限共有八组，构成正八面体，简称八面体面。八面体表面上的应力为八面体应 力。因为有： 1=,=h5==5 由式(2.7)，式(2.12)，有： a=5@,-0+o,-0,+o,-0 借助于I1,I2,又有： a=o,+0,+a)=0。= (2.17) =号厅+ =}a,-,P+(a,-o,P+(a.-a,P+6g+r2+臣）(2.18) 为了使不同应力状态具有可比性，定义了等效应力·。（应变能相同的条件 下)，也称相当应力

值得一提的是，  m ij 只影响体积变化，不影响形状变化，但它关系到材料 塑性的充分发挥。三向压应力有利于材料塑性的发挥。 应力偏张量仍然 是一个二 阶对称张量 ，同样有三 个不变量 ，分别为 1 2 3 I' , I' , I' 。          = = − + − + − + + + = + + = i j x y y z z x xy yz z x x y z I I I ' ' ( ) ( ) ( ) 6( ) 6 1 ' ' ' ' ' 0 3 2 2 2 2 2 2 2 1              （2.16） I' 1 = 0 表明应力偏张量已不含平均应力成份。 2 I' 与屈服准则有关（见第二 章），反映了物体形状变化的程度。 3 I' 反映了变形的类型： I' 3  0 表示广义拉伸 变形； 3 I' =0 表示广义剪切变形， 3 I' <0 表示广义压缩变形。 1.2.5 八面体应力与等效应力 在主应力空间中，每一掛限中均有一组与三个坐标轴成等倾角的平面，八个 掛限共有八组，构成正八面体，简称八面体面。八面体表面上的应力为八面体应 力。因为有： 3 1 l 1 = l 2 = l 3 = l =  由式（2.7），式（2.12），有： 2 3 1 2 2 3 2 8 1 2 ( ) ( ) ( ) 3 1  =  − +  − +  − 借助于 I1， I2，又有： 8 1 3 1 ( ) 3 1 I  =  x +  y +  z = m = （2.17） 2 2 8 1 3 3 2  = I + I ( ) ( ) ( ) 6( ) 3 1 2 2 2 2 2 2 x y y z z x xy yz z x =  − +  − +  − +  + + （2.18） 为了使不同应力状态具有可比性，定义了等效应力  e （应变能相同的条件 下），也称相当应力

=方@，-，八+o,-a+a-a+《号+g+百2.19 至此，由0.=。(ogl,=f(o,) 引出了三种特殊应力面，如图2-4所示。它 们是： 【：三组主平面，应力空间中构成平行 六面体。 01比 Ⅱ：六组主切平面，在应力空间构成十 图24应力球与特殊面 二面体。 Ⅲ：四组八面体面，构成正八面体

8 2 3  =  e ( ) ( ) ( ) 6( ) 2 1 2 2 2 2 2 2 x y y z z x xy yz z x =  − +  − +  − +  + + （2.19） 至此，由 ( , ), ( , ) n ij i n ij i  f  l  f  l =  =  引出了三种特殊应力面，如图 2-4 所示。它 们是： Ⅰ：三组主平面，应力空间中构成平行 六面体。 Ⅱ：六组主切平面，在应力空间构成十 二面体。 Ⅲ：四组八面体面，构成正八面体。 图 2-4 应力球与特殊面

第三讲工程塑性理论 教学内容： 本章讨论了应力平衡微分方程一直角坐标下的平衡微分方程，柱坐标系、 球坐标系下的平衡微分方程 教学重点： 直角坐标下的平衡微分方程，柱坐标系、球坐标系下的平衡微分方程 教学难点： 直角坐标下的平衡微分方程，柱坐标系、球坐标系下的平衡微分方程 教学方法： 课堂教学为主，结合多媒体教学。 教学要求： 重点掌握直角坐标下的平衡微分方程 教学时间： 直角坐标下的平衡微分方程50mi:柱坐标系、球坐标系下的平衡微分方程 50min: 4.1应力平衡微分方程 应力平衡微分方程就是物体任意无限相邻二点间：关系，可以通过微体沿坐 标轴力平衡来得到，一般应力平衡方程在不同坐标系下有不同的表达形式。 4.1.1直角坐标下的平衡微分方程 假设物体为连续介质。无限邻近二点的应力状态分别为，：，少)， ,x+,y+,:+山)（见图2-8）。假设0的连续可导则有 假设‘g连续可导，则有 G,g+++)=a,+Ck,k=X列】 列六面体力平衡，则有

第三讲 工程塑性理论 教学内容： 本章讨论了应力平衡微分方程——直角坐标下的平衡微分方程，柱坐标系、 球坐标系下的平衡微分方程 教学重点： 直角坐标下的平衡微分方程，柱坐标系、球坐标系下的平衡微分方程 教学难点： 直角坐标下的平衡微分方程，柱坐标系、球坐标系下的平衡微分方程 教学方法： 课堂教学为主，结合多媒体教学。 教学要求： 重点掌握直角坐标下的平衡微分方程 教学时间： 直角坐标下的平衡微分方程 50min；柱坐标系、球坐标系下的平衡微分方程 50min； 4.1 应力平衡微分方程 应力平衡微分方程就是物体任意无限相邻二点间  ij 关系，可以通过微体沿坐 标轴力平衡来得到，一般应力平衡方程在不同坐标系下有不同的表达形式。 4.1.1 直角坐标下的平衡微分方程 假设物体为连续 介质。无限邻 近二点的应 力状态分别 为 (x, y,z)  ij ， (x dx,  ij + y + dy,z + dz) （见图 2-8）。假设  ij 的连续可导则有 假设  ij 连续可导，则有 ( d , d , d ) ( , , ) d (i, j, k = x, y, z)   + + + = + k k i j i j i j x x x x y y z z x y z    列六面体力平衡，则有