
一、X射线形貌学的概念 第三章X-射线形粮分析技术 一、X射线形貌学的摄念 含义 二、形貌学实脸技术 ()取向村度形貌技术 X射线形粮半,又称为X射线粮相学或射线粮相术(X可 (2)透射投形貌术 Diffraction Topography,or,X-ray Topography), (3)反射形貌术 称X射线形貌术。 三、X射线形貌学的发展现状 一束X射线在品体中向一定方向传播时,当其到达晶体的出光面时,由于干涉效 应会出现干涉条纹,如果晶体中存在缺陷,这些干涉条纹和缺陷象会一起叠加在 均匀的背景上,形成特征的衍衬形貌。通过对这种而衬形貌的研究,逐渐建立了X 射线衍射学的一个分支和技术,即以射线形貌学(貌相术或貌相学)。 盘由:者线吊术不华华是将欢安的,它所究的毛发生新新的省国的形 应用: 利用X-射线形貌术(貌相术或貌相学),可以分析 形貌的衬度变化情况和规律,从而可以探明晶体的 完整程度,测定缺陷的种类、分布、组态、密度以 及应变矢量和其指向等等,进而能够了解晶体的生 长规律,研究缺陷的成因、增殖、运动、交互作 200地 用,以及控制和消除的途径。多年来,X射线形貌 技术己经成为研究近完整晶体中各种类型缺陷的一 a)Back refle raph and (b)tra hecotioama6sC 种十分有效而重要的手段。往往根据一张X射线形 arch Inc.) ons lying perper 貌图上的衬度分析就可以确定不同类型的缺陷。 Materias Sciencen Semiconductor Processing9(2006)315-322,Department of 历史: 1931年,Bg用单色辐射拍摄岩盐解理面的表面反射衍射象,观察到了与滑移 对应的条纹。 1943年,Barrettx对Berg的方法进行了政进,得到了更加佳的效果,能够看到象 中的许多衍衬细节。由此,人们开始注意到了X-射线衍衬形貌 1944年,Ramachandran利用多色辐射进行了透射形貌象观测,成为X-射线形貌 的研究平。 上世纪五十年代,随着半导体、激光、红外等科学技术的兴起,对高质量品体的 要求越来越严格,X-射线由于其无损性面被大力发展。 1958年左右,Lang和Borrmann分别发展了投影貌相术和异常透射貌相术: Bonse与Kappler继Bond与Andrus.之后发展了双品衍射仪方法:Newkirk也将B-B 法在技术上加以完善. 1965年,Bonse与Hart发明了X射线干涉仪.从六十年代后,X射线形貌学在原 理、方法、设备和应用等方面均得到了高速发展,使这门学科和技术日臻完善
第三章 X-射线形貌分析技术 一、X-射线形貌学的概念 二、形貌学实验技术 (1)取向衬度形貌技术 (2)透射投影形貌术 (3)反射形貌术 三、X-射线形貌学的发展现状 含义 X-射线形貌学,又称为X-射线貌相学或X-射线貌相术( X-ray Diffraction Topography Diffraction Topography Diffraction Topography Diffraction Topography,or ,X-ray Topography X-ray Topography X-ray Topography X-ray Topography),简 称X射线形貌术。 一束X-射线在晶体中向一定方向传播时,当其到达晶体的出光面时,由于干涉效 应会出现干涉条纹,如果晶体中存在缺陷,这些干涉条纹和缺陷象会一起叠加在 均匀的背景上,形成特征的衍衬形貌。通过对这种衍衬形貌的研究,逐渐建立了X 射线衍射学的一个分支和技术,即X-射线形貌学(貌相术或貌相学)。 应该指出: X-射线形貌术不单单是研究表面的,它研究的是发生衍射的衍射面的形 貌。 一、X-射线形貌学的概念 (a) Back reflection topograph and (b) transmission topograph recorded from a 6H-SiC basal plane wafer (grown by Cree Research Inc.). Note the dislocation loops lying on the basal plane, and their interaction with the screw dislocations lying perpendicular to the basal plane. (Materials Science in Semiconductor Processing 9 (2006) 315 –322, Department of Materials Science and Engineering, State University of New York at Stony Brook, Stony Brook, NY 11794-2275, USA) 应用: 利用X-射线形貌术(貌相术或貌相学),可以分析 形貌的衬度变化情况和规律,从而可以探明晶体的 完整程度,测定缺陷的种类、分布、组态、密度以 及应变矢量和其指向等等,进而能够了解晶体的生 长规律,研究缺陷的成因、增殖、运动、交互作 用,以及控制和消除的途径。多年来,X射线形貌 技术已经成为研究近完整晶体中各种类型缺陷的一 种十分有效而重要的手段。往往根据一张X射线形 貌图上的衬度分析就可以确定不同类型的缺陷。 历史: 1931年,Berg用单色辐射拍摄岩盐解理面的表面反射衍射象,观察到了与滑移 对应的条纹。 1943年,Barrett对Berg的方法进行了改进,得到了更加佳的效果,能够看到象 中的许多衍衬细节。由此,人们开始注意到了X-射线衍衬形貌。 1944年,Ramachandran利用多色辐射进行了透射形貌象观测,成为X-射线形貌 学的研究开端。 上世纪五十年代,随着半导体、激光、红外等科学技术的兴起,对高质量晶体的 要求越来越严格,X-射线由于其无损性而被大力发展。 1958年左右,Lang和Borrmann分别发展了投影貌相术和异常透射貌相术; Bonse与Kappler继Bond与Andrus之后发展了双晶衍射仪方法;Newkirk也将B-B 法在技术上加以完善。 1965年,Bonse与Hart发明了X射线干涉仪。从六十年代后,X射线形貌学在原 理、方法、设备和应用等方面均得到了高速发展,使这门学科和技术日臻完善
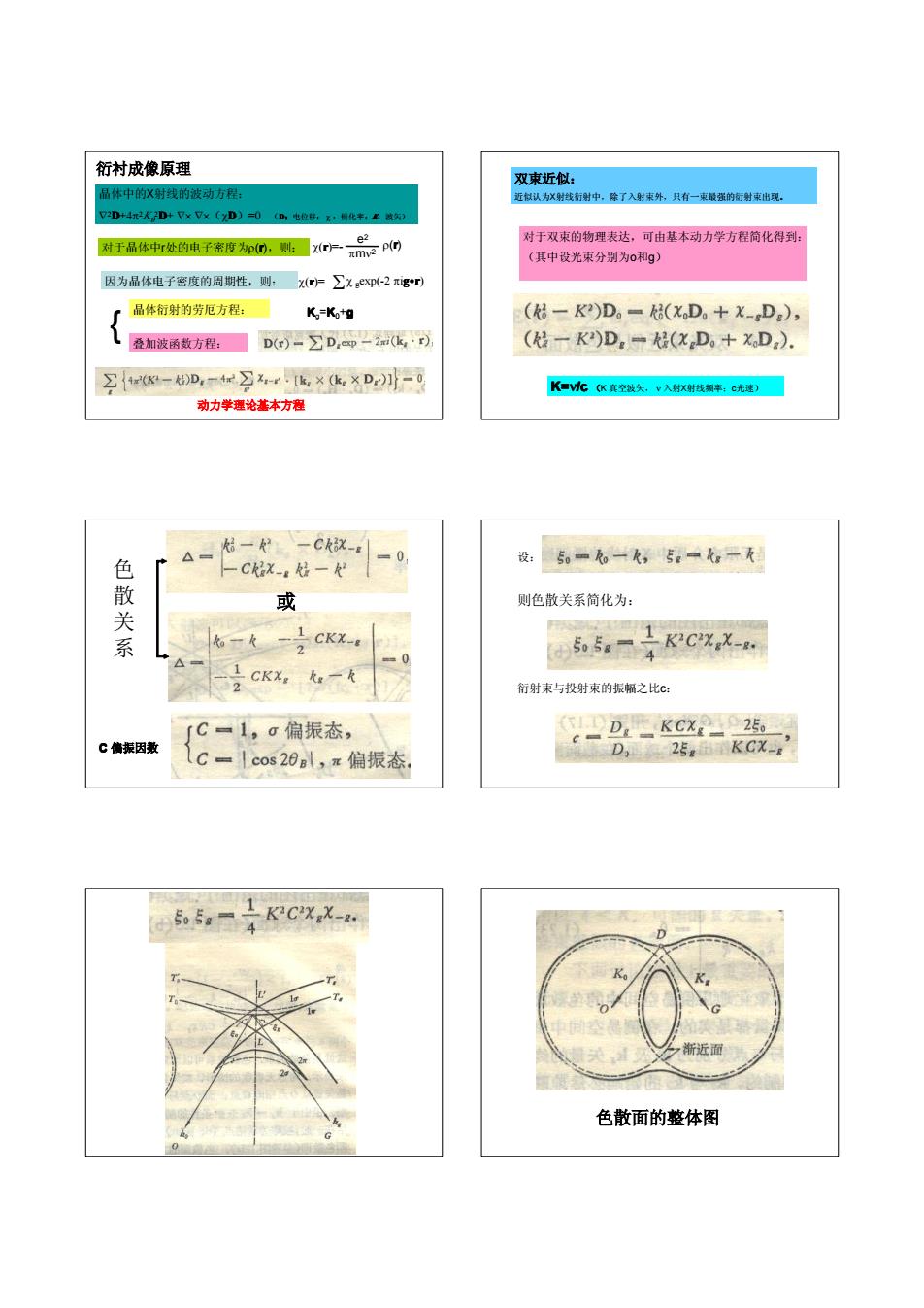
衍村成像原理 双束近似: 品体中的X射线的波动方 近献认为X射线行谢中,除了入射束外,只有一束最强的标射束出现, 7D+42人D+V×7×(D)=司(D,电位5:z:最化本:k被实) 对于晶体中r处的电子密度为00,则:Xp0 对于双束的物理表达,可由基本动力学方程简化得到: (其中设光束分别为0和g) 因为晶体电子密度的周期性,则:X片∑xp(-2πgr) 晶体行射的劳厄方程: K=Ko+g (格一K)D。=8(xD。+X-D), 叠加波函数方程:■D()-∑D,即一2m(k,·p (0一K)Dg=(xD+XD). 2{*K-心D,r2xr6,×k,×D]-0 KC(K真空波矢,v入射X射线湖率:c光速) 动力学理论基本方程 k8一一C- △= =0 设:50=k。一k,5。一九。= 一C经x-。好一 色散关系 或 则色散关系简化为: k一 1 CKX- 、2 505g= 1KCXX-8. =0 1 2 CKXg一 衍射束与投射束的振幅之比c: C=1,偏振态, D=Kcx2-2。 C C偏振因数 Icos28a,π偏振态, D,25,Kcx’ 505g= 1 KCX X-8. 4 渐近面 色散面的整体图
衍衬成像原理 晶体中的X射线的波动方程: ∇2D+4π2K0 2D+ ∇× ∇×(χD)=0 (D:电位移; χ :极化率;K:波矢) e2 πmν2 χ ρ(r) (r)=- Kg=K0+g 对于晶体中r处的电子密度为ρ(r),则: 因为晶体电子密度的周期性,则: χ(r)= Σχ gexp(-2 πig•r) 叠加波函数方程: 晶体衍射的劳厄方程: { 动力学理论基本方程 双束近似: 近似认为X射线衍射中,除了入射束外,只有一束最强的衍射束出现。 对于双束的物理表达,可由基本动力学方程简化得到: (其中设光束分别为o和g) K=ν/c (K 真空波矢, ν 入射X射线频率;c光速) 或 色 散 关 系 C 偏振因数 设: 则色散关系简化为: 衍射束与投射束的振幅之比c: 色散面的整体图

双光束的波场 D-D+D, 设真空入射波为: D=D exp→2ri(Kgr)] 在入光面处,存在边界条件: 0=D9+Dg, 昂体中的Bloch波为: D-D,exp-[2vi(kr)]+D expl-2mi(kr)] P-±am 则: 则在色散面上入射光和衍射光的振幅之比为: 9-a+e 1 可以看出当y,+0,衍射光束的振髓都等于零D9一0,而 2X)C -0-0-别 D。一D,D一0,只剩单一分支的D。,当y→-o0,情况也 Y y-2cx(,/ 相似,过渡到单一光束。当y一0,即正好满足布喇格条件时, Diexp(-)+Dexp(-2xi D/D 在出光面处,边 界条件: Di exp(-2xik), 1.0. (包括光穿过厚度为的片 DO exp(-2xitk)+D exp(-2witk) 0.9 所引起的位相因子) DD =D exp(-2xik), 式中D与D呼为从出光面进人真空的通射光束和衍射光桌的碳幅, D/D 07 0-器-1+r+w+ -0.1 求得透射系数T -5-4-3-2-1012343y 和反射系数R为 5”10”151 KC 晶体中振幅比的变化情况.C=1 其中: TMAMM 2.5引 2.0 1.5 1.0 0.5 246810121404 图1.8衍射职分强度随4的变化
双光束的波场 设真空入射波为: 晶体中的Bloch波为: 则在色散面上入射光和衍射光的振幅之比为: 在入光面处,存在边界条件: 则: 在出光面处,边 界条件: (包括光穿过厚度为t的晶片 所引起的位相 因子) 其中: 求得透射系数T 和反射系数R为:

球面波及晴变晶体的波动方程 D(r)->Di(r)exp(-i2x(r)) s(r)-ke.r-g u(ro), 其中D(r)表示畸变晶体的波场振幅S畸变矢量 ()是在:点的子由于酸变从坐标1移至r时的位移变量,是原子畸变能的初始位凰矢量, -r-r。+u(ro), vs(r)=k-v(g·u) 完整晶体的衍衬象 8D6 inKCX-D3, 售食寒 投射光束和衍射光束的振幅分别是 05g 8Ds -inKCX,D(+i2πKBDg D,-二会K 2 85 在y=0的平面内,衍射光强度: 高木方程组 1,-0%D=D,+D%+2D,D。·eo2K-Kn 高木方程表明,当晶体中存在畸变 时,光振幅将随着畸变发生变化。 -}at二aaKK)- 表明二者波场的千沙均随品体厚度·是周期变化,其周期大小为 (K,-K)n-A(1+n [A(1+可)];显见,它们在习一0时达般大,也即在严格的 布喇格条件时所对应的周期大小正是消光距离,流量这:中元 ↓ ,=A6=cos0()广品 +高¥的并的区死甲 =x八cos8a/2c(FF)n 1g-sin[πAr(1+2)]/(1千7). 晶体在X射线貌相上 同样,入射光的强度: 显示衍衬干涉条纹是 1。-eos21x4(1+)]/+), 完整性高的一种标志。 Ag:色散面的直径: n:偏差参数(n=2sin0sec01Ao.0布拉格角)
球面波及畸变晶体的波动方程 Sg畸变矢量 ) 高木方程表明,当晶体中存在畸变 时,光振幅将随着畸变发生变化。 完整晶体的衍衬象 在y=0的平面内,衍射光强度: 同样, 入射光的强度: Λ0:色散面的直径; η:偏差参数(η=2sinθsecθ/Λ0, θ布拉格角 ) 晶体在X射线貌相上 显示衍衬干涉条纹是 完整性高的一种标志

位错的行衬象: 位错衍衬象有 三种: ()中0 直接象: d 动力学象: 中间象 Materials Science and Engineering A319-321 (2001)152-155 二缝 Dislcation mutiplication during the very first stages of plastic deformation in siicon observed by X-ray topography 图2,位的三孙象的几何 位错消象现象和规律 动力学衍射理论求解位错象衬度的严格解是困难的 用位错应变杨分布和完整晶体摆动曲线宽度求出有关位错的直接 象的一定范围胡是可以的,或者直接用位错线周园的应变场,在双 光束近似下求解高木方程的数值解也是可能的 mm g(d) 0 A(100微87商648aoo Materials Science and Engineering B87 (2001)173-177 Partial dislocations in the X-ray of as-grown hexaoonal siicon carbide crystals ,p)-2一bptb4- sin 2o +b×1651+2} 位错衍衬象的宽度为国 2(1-#) (的 Wasu -Fa(g'b)/2x, 单为泊松比,]为位错线走向的单位矢量 C-Pn-0.88 ).d 螺位错消象判据: gu=0或g·b=0 刃位错消象判据: g·b=0和g·b×1=0
位错的衍衬象: 位错衍衬象有 三种: 直接象; 动力学象; 中间象 Materials Science and Engineering A319 –321 (2001) 152–155 Dislocation multiplication during the very first stages of plastic deformation in silicon observed by X-ray topography Fig. 1. Synchrotron white-beam X-ray topographs of a PVT 4H–SiC wafer showing basal plane dislocations. (a) g=1210 (=0.59 A ); ( b)g=1100 (=0.74 A ); (c) g=1010; (d) g=0110. Materials Science and Engineering B87 (2001) 173 –177 Partial dislocations in the X-ray topography of as-grown hexagonal silicon carbide crystals 位错消象现象和规律: 螺位错消象判据: 刃位错消象判据: