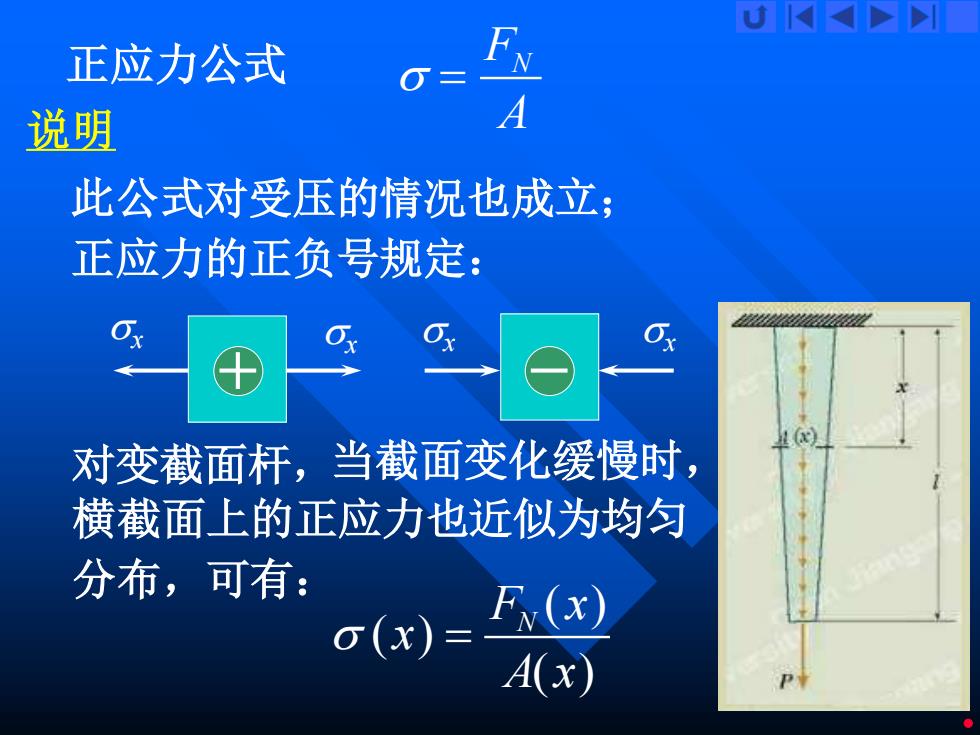
U K 正应力公式 说明 A 此公式对受压的情况也成立; 正应力的正负号规定: 对变截面杆,当截面变化缓慢时, 横截面上的正应力也近似为均匀 分布,可有: (x)= Fv(x) A(x)
12 正应力公式 FN A = 说明 此公式对受压的情况也成立; 正应力的正负号规定: 横截面上的正应力也近似为均匀 分布,可有: 对变截面杆, x x x x ( ) ( ) ( ) F x N x A x = 当截面变化缓慢时

圣维南原理(Saint--Venant principle.) 100 根据圣维南原理,对弹性 100 体某一局部区域的外力系,若 0目 用静力等效的力系来代替;则 288 210 力的作用点附近区域的应力分 180 100 E.N 布将有显著改变,而对略远处 其影响可忽略不计。 565 425 理论分析与实验证明,影 100 响区的轴向范围约为杆件一个 横向尺寸的大小。 13
13 圣维南原理(Saint-Venant principle) 根据圣维南原理,对弹性 体某一局部区域的外力系,若 用静力等效的力系来代替;则 力的作用点附近区域的应力分 布将有显著改变,而对略远处 其影响可忽略不计。 理论分析与实验证明,影 响区的轴向范围约为杆件一个 横向尺寸的大小
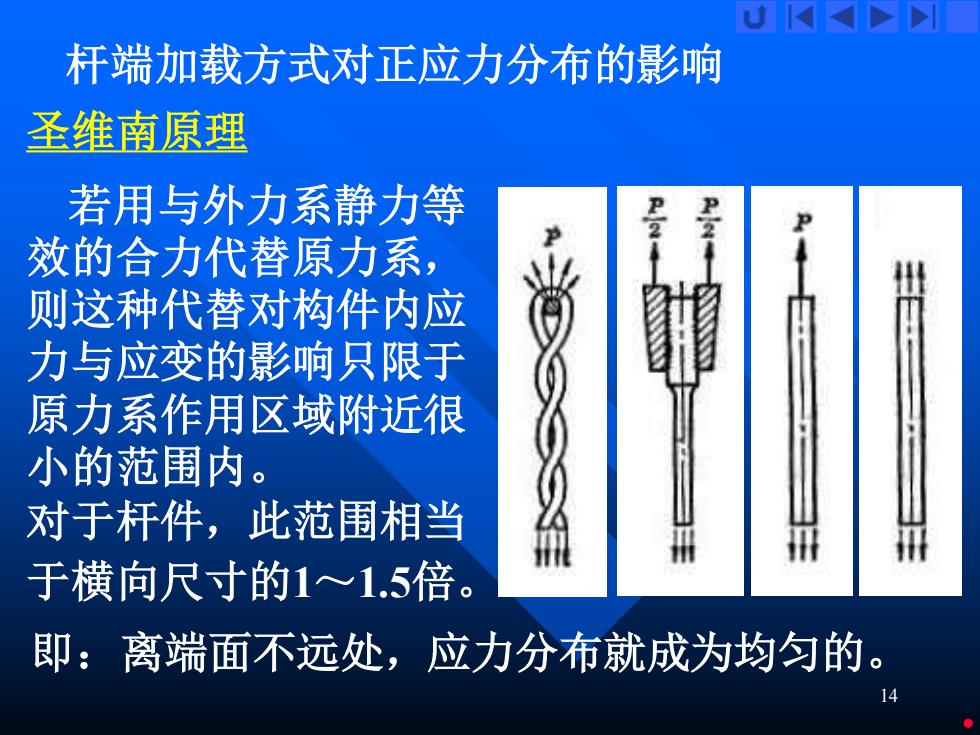
N> 杆端加载方式对正应力分布的影响 圣维南原理 若用与外力系静力等 效的合力代替原力系, 则这种代替对构件内应 力与应变的影响只限于 原力系作用区域附近很 小的范围内。 对于杆件,此范围相当 于横向尺寸的1~1.5倍。 即:离端面不远处,应力分布就成为均匀的
14 杆端加载方式对正应力分布的影响 圣维南原理 若用与外力系静力等 效的合力代替原力系, 则这种代替对构件内应 力与应变的影响只限于 原力系作用区域附近很 小的范围内。 对于杆件,此范围相当 于横向尺寸的1~1.5倍。 即:离端面不远处,应力分布就成为均匀的
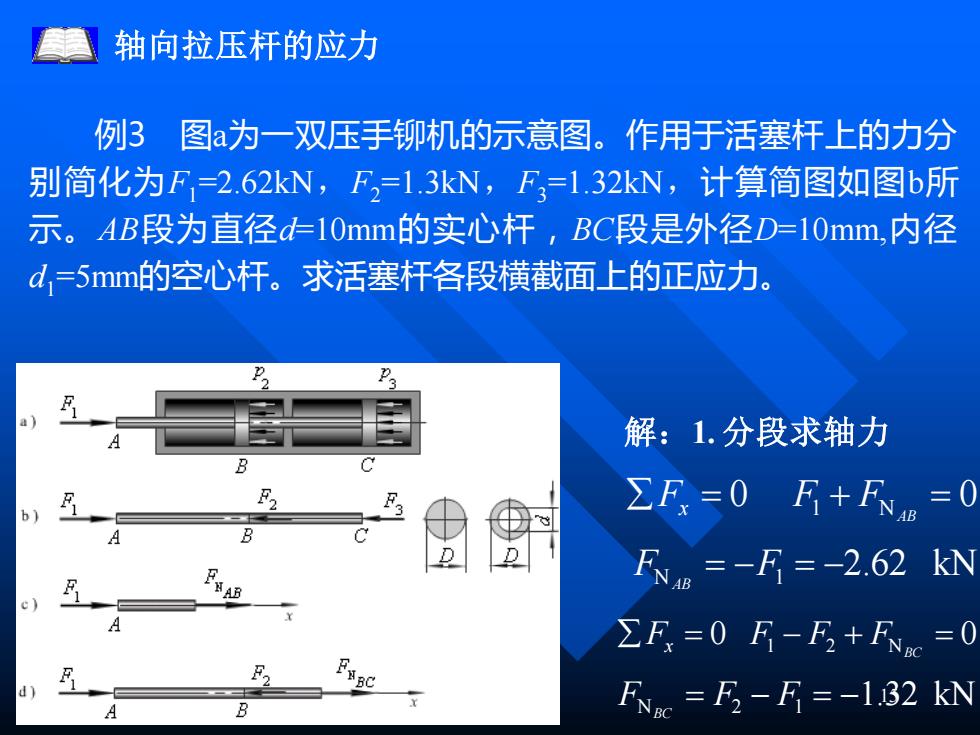
轴向拉压杆的应力 例3图a为一双压手铆机的示意图。作用于活塞杆上的力分 别简化为F=2.62kN,F2=1.3kN,F3=1.32kN,计算简图如图b所 示。AB段为直径dl0mm的实心杆,BC段是外径D=10mm,内径 d,=5mm的空心杆。求活塞杆各段横截面上的正应力。 解:1.分段求轴力 ΣF=0F+FNB=0 R=-F=-2.62kN AB ∑F=0F-F2+Fx=0 BC FNiC =F2-F=-1.32 kN
15 轴向拉压杆的应力 解:1. 分段求轴力 0 0 = 1 + N = AB Fx F F FN = −F1 = −2.62 kN AB = 0 1 − 2 + N = 0 BC Fx F F F FN = F2 − F1 = −1.32 kN BC 例3 图a为一双压手铆机的示意图。作用于活塞杆上的力分 别简化为F1 =2.62kN,F2 =1.3kN,F3 =1.32kN,计算简图如图b所 示。AB段为直径d=10mm的实心杆,BC段是外径D=10mm,内径 d1 =5mm的空心杆。求活塞杆各段横截面上的正应力
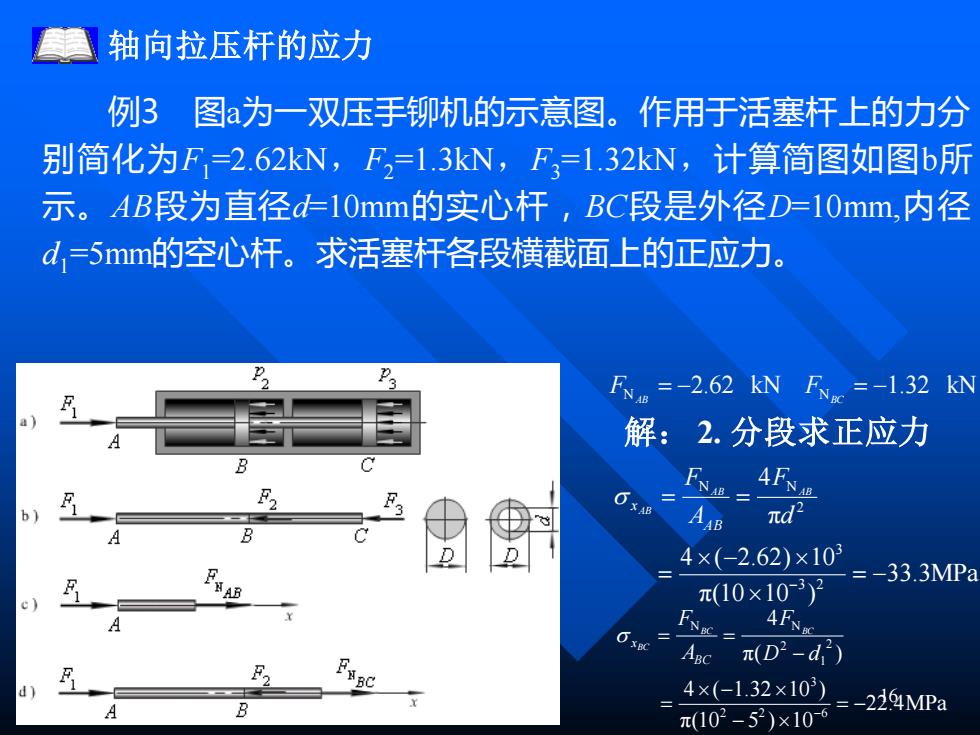
轴向拉压杆的应力 例3图a为一双压手铆机的示意图。作用于活塞杆上的力分 别简化为F=2.62kN,F,=1.3kN,F3=1.32kN,计算简图如图b所 示。AB段为直径d=10mm的实心杆,BC段是外径D=10mm,内径 d,=5mm的空心杆。求活塞杆各段横截面上的正应力。 F=-2.62kNF=-1.32N 解:2.分段求正应力 B AAB nd2 4×(-2.62)×103 =-33.3MPa π(10×10-32 0= AFNRC Acπ(D2-d BC 4×(-1.32×103) B =-2264MPa π(102-52)×10-6
16 轴向拉压杆的应力 N = −2.62 kN N = −1.32 kN AB BC F F 33.3MPa π(10 10 ) 4 ( 2.62) 10 π 4 3 2 3 2 N N = − − = = = − d F A F AB AB AB AB x 22.4MPa π(10 5 ) 10 4 ( 1.32 10 ) π( ) 4 2 2 6 3 2 1 2 N N = − − − = − = = − D d F A F BC BC BC BC x 例3 图a为一双压手铆机的示意图。作用于活塞杆上的力分 别简化为F1 =2.62kN,F2 =1.3kN,F3 =1.32kN,计算简图如图b所 示。AB段为直径d=10mm的实心杆,BC段是外径D=10mm,内径 d1 =5mm的空心杆。求活塞杆各段横截面上的正应力。 解: 2. 分段求正应力