
例1 已知:F=40kN, F,2 F2=30kN,F3=20 B kN。 求:1-1,2-2和33截面的轴力,并作杆的轴力图。 解:1-1截面,取右边,受力如图。 ∑x=0 F3 FNI=F+F2-Fs B =50(kN) D 2-2截面,取右边,受力如图
7 例 1 已知:F1=40kN, F2=30kN, F3=20 kN。 解: X = 0 1 1 2 2 3 3 F1 F2 F3 A B C D 1-1截面,取右边,受力如图。 求:1-1, 2-2和3-3截面的轴力, 并作杆的轴力图。 1 1 F1 F2 F3 B C D FN1 FN1 1 2 3 = + − F F F = 50(kN) 2-2截面, 取右边, 受力如图。 2 2 F2 F3 C D FN2
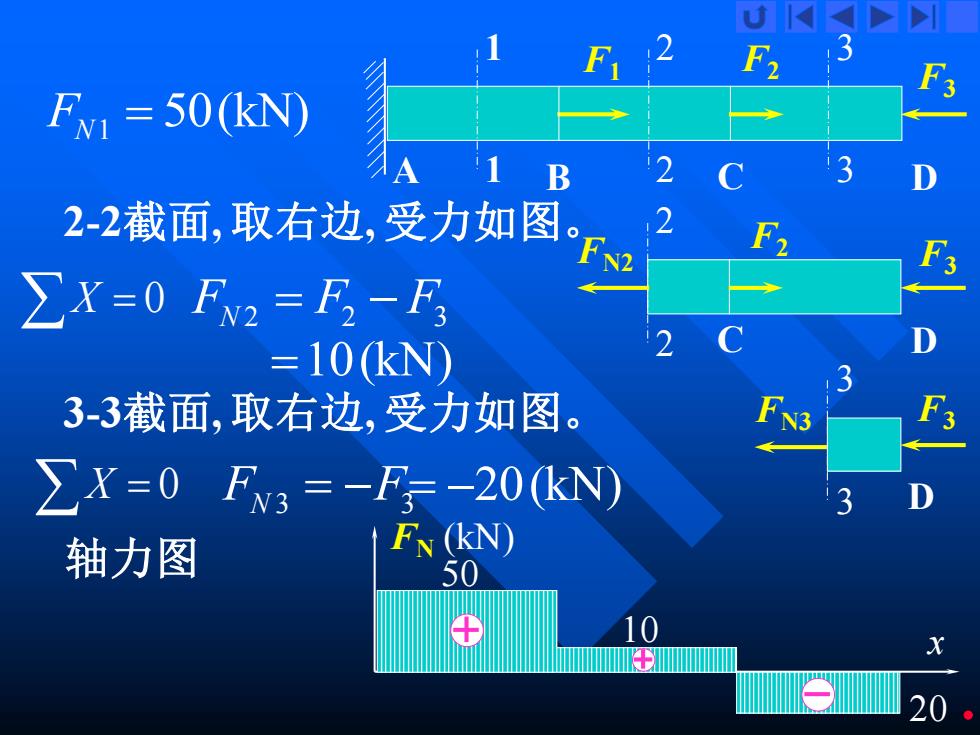
F12 FN1=50(kN) B 2-2截面,取右边,受力如图 F ∑X=0F2=F-F =10kN 3-3截面,取右边,受力如图。 N3 ∑X=0F3=-F-20kN) 轴力图 ↑FN(kN) 50
8 X = 0 1 1 2 2 3 3 F1 F2 F3 A B C D FN3 F F F N 2 2 3 = − =10(kN) 2-2截面, 取右边, 受力如图。 2 2 F2 F3 C D FN2 3-3截面, 取右边, 受力如图。 3 3 F3 X = 0 F F N3 3 = − = −20(kN) D 轴力图 x FN (kN) 50 10 20 1 50(kN) FN =
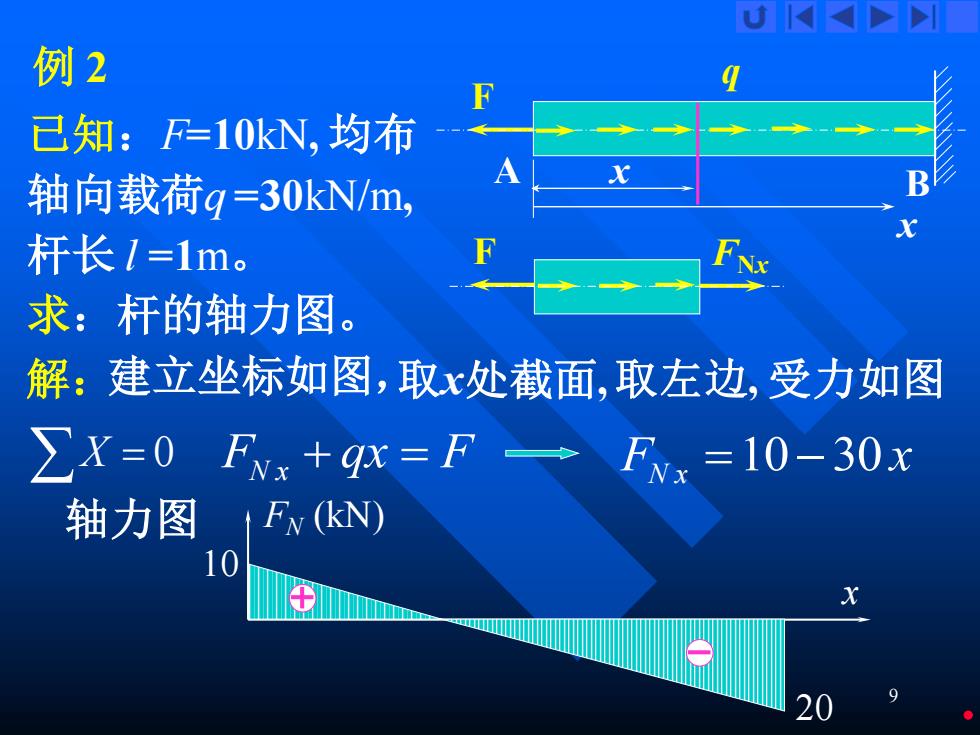
D> 例2 F 已知:F=10kN,均布 轴向载荷g=30kN/m, 杆长1=1m。 F 求:杆的轴力图。 解:建立坐标如图,取x处截面,取左边,受力如图 ∑X=0Fx+qx=F一Fx=10-30x 轴力图Fv(kN) 10
9 例 2 已知:F=10kN, 均布 轴向载荷q =30kN/m, 杆长 l =1m。 解:建立坐标如图, 求:杆的轴力图。 q F A B 取x处截面,取左边, 受力如图 x x F FNx X = 0 F qx F N x + = 10 30 F x N x = − 轴力图 x FN (kN) 10 20
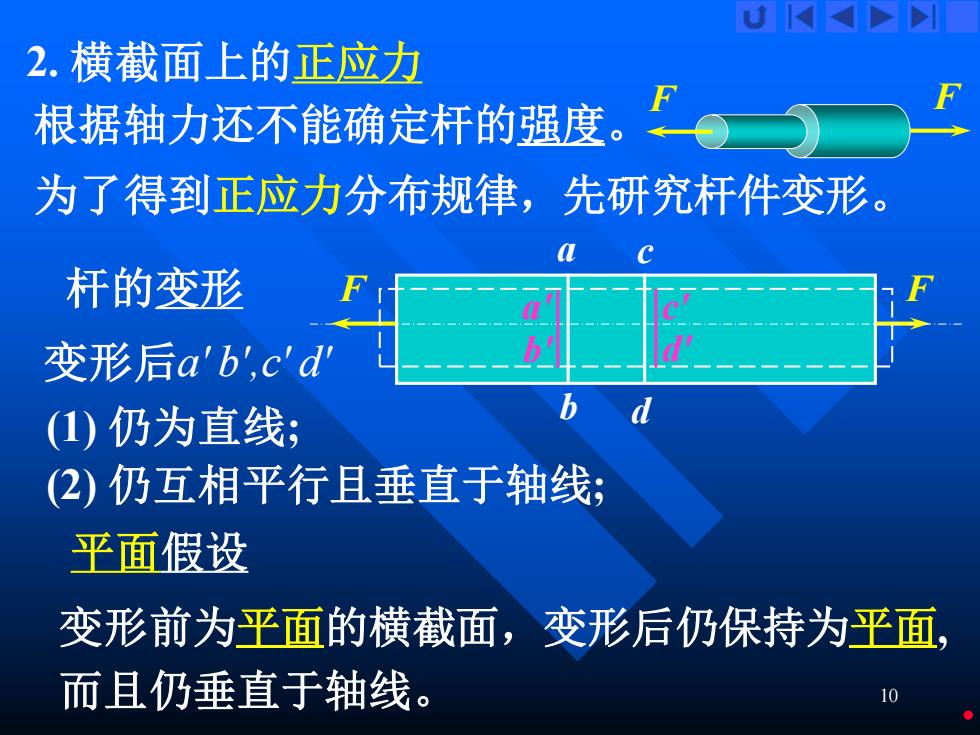
2.横截面上的正应力 根据轴力还不能确定杆的强度。 为了得到正应力分布规律,先研究杆件变形。 杆的变形 变形后ab',c'd (1)仍为直线; (2)仍互相平行且垂直于轴线; 平面假设 变形前为平面的横截面,变形后仍保持为平面, 而且仍垂直于轴线。 10
10 2. 横截面上的正应力 根据轴力还不能确定杆的强度。 为了得到正应力分布规律,先研究杆件变形。 杆的变形 变形后a' b',c' d' F F F a b d' F a' b' c' c d 变形前为平面的横截面,变形后仍保持为平面, 而且仍垂直于轴线。 (1) 仍为直线; (2) 仍互相平行且垂直于轴线; 平面假设
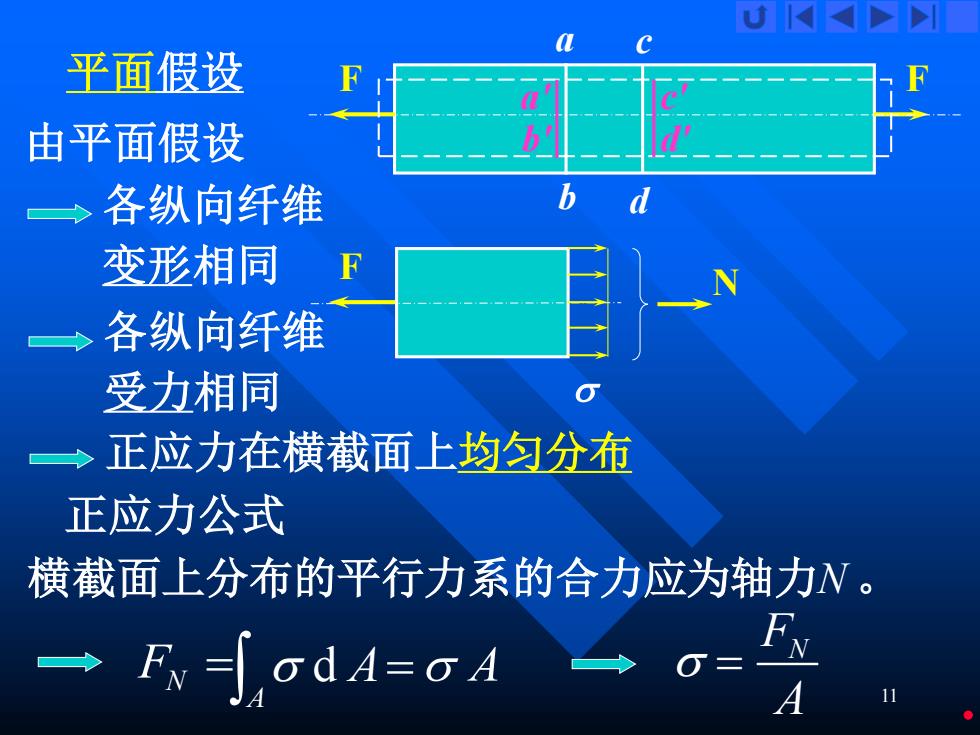
K 平面假设 由平面假设 各纵向纤维 变形相同 F 各纵向纤维 受力相同 正应力在横截面上均匀分布 正应力公式 横截面上分布的平行力系的合力应为轴力N。 → RσdA=oA A
11 F N F a b d' F a' b' c' c d 由平面假设 平面假设 各纵向纤维 变形相同 各纵向纤维 受力相同 正应力在横截面上均匀分布 横截面上分布的平行力系的合力应为轴力N 。 FN = 正应力公式 d A= A A FN A =