轴向拉压杆的应力 例4直径为d长为1的圆截面直杆,铅垂放置,上端固定, 如下图所示。若材料单位体积质量为p,试求因自重引起的杆的 轴力和最大正应力。 解: F(x)=qx=pg X '耳2a 轴力方程 F(x) 作轴力图 % 2 22 最大轴力 4 最大应力 Xmax FNs二pg A17
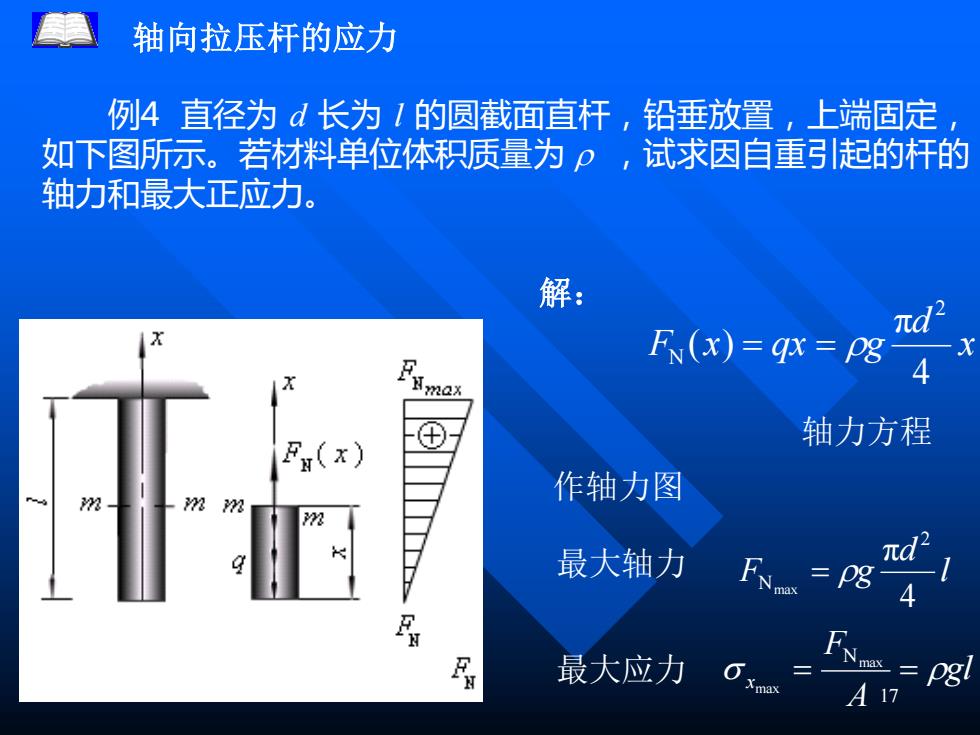
17 轴向拉压杆的应力 例4 直径为 d 长为 l 的圆截面直杆,铅垂放置,上端固定, 如下图所示。若材料单位体积质量为 ,试求因自重引起的杆的 轴力和最大正应力。 轴力方程 作轴力图 最大轴力 最大应力 x d F x qx g 4 π ( ) 2 N = = l d F g 4 π 2 Nmax = gl A F x = = max max N 解:

U K §2.3直杆轴向拉伸或压缩时 斜截面上的应力了解 有时拉(压)杆件沿斜截面发生破坏。 因此,需要确定斜截面上的应力。 横截面上的正应力: F A A 斜截面k-k 应力仍为均匀分布 内力仍为F F。=F 斜截面面积:A2=A/CoSo
18 §2. 3 直杆轴向拉伸或压缩时 斜截面上的应力(了解) 有时拉(压)杆件沿斜截面发生破坏。 横截面上的正应力: F F k k FN a A = F A = F Fa k k 斜截面k-k 应力仍为均匀分布 内力仍为F F F a = 斜截面面积: Aa = A/ cosa 因此,需要确定斜截面上的应力

斜截面kk 应力仍为均匀分布 内力仍为F F,= F 斜截面面积: A=A/cosa 斜截面上的全应力: F Pa= cosa=ocosa A A 斜截面上的正应力和切应力 Oa=pa cosa=o cos a Ta=Pasm a=osin acosa O sin 2a 2
19 k k F Fa 斜截面k-k 应力仍为均匀分布 内力仍为F F F a = 斜截面面积: Aa = A/ cosa 斜截面上的全应力: F p A a a a = F Aa = pa a ta a cos F A = a = cosa a 斜截面上的正应力和切应力 a = pa cosa a 2 = cos t a = pa sin a = sina cosa a sin 2 2 =

α角斜截面上的正应力和切应力 =ocos-a sin 2a 正负号规定 的正负号:从横截面的法线到斜截面的法 线,逆时钍为正,顺时针为负。 o。的正负号:拉应力为正,压应力为负。 t。的正负号:绕所保留的截面,顺时针为正, 逆时针为负。 讨论 20
20 pa a ta a a a角斜截面上的正应力和切应力 a a 2 = cos a t a sin 2 2 = 正负号规定 a的正负号: ta的正负号: 从横截面的法线到斜截面的法 线,逆时针为正,顺时针为负。 a的正负号: 拉应力为正,压应力为负。 绕所保留的截面,顺时针为正, 逆时针为负。 讨论

U K α角斜截面上的正应力和切应力 g。=ocos-a sin 2a 讨论 =0°时(横截面): O=0 Ta=0 o=45°(斜截面): a max 2 =90°(纵向截面):g。=0 结论:omx发生在横截面上 max tm发生在c=45斜截面上,tm=/2
21 Fa a ta a a a角斜截面上的正应力和切应力 a a 2 = cos a t a sin 2 2 = 讨论 a=0时(横截面): a = a max t a = 0 a=45(斜截面): , 2 a = a a max t =t =, 2 = a=90(纵向截面): = 0, a t a = 0 结论: max 发生在横截面上, tmax发生在a=45斜截面上, max = t max = / 2