杭州电子科技大学：《计算机视觉》课程教学资源（PPT课件讲稿）第三讲 图像预处理

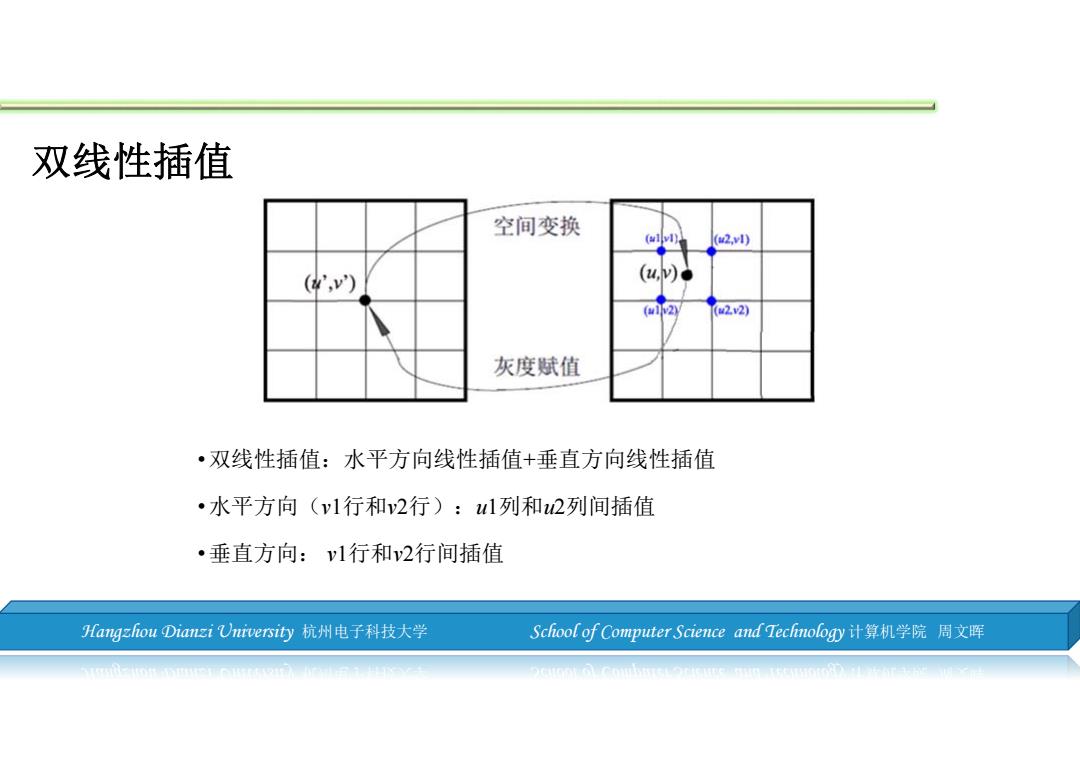
双线性插值 空间变换 (wl vl) (a2,v) (',) (u,)d (2 (2.2) 灰度赋值 •双线性插值：水平方向线性插值+垂直方向线性插值 ·水平方向(v1行和2行)：1列和2列间插值 ·垂直方向：v1行和2行间插值 Hangzhou Dianzi University杭州电子科技大学 School of Computer Science and Tecfnology计算机学院周文晖

Hangzhou Dianzi University 杭州电子科技大学 School of Computer Science and Technology 计算机学院 周文晖 双线性插值 •双线性插值：水平方向线性插值+垂直方向线性插值 •水平方向（v1行和v2行）：u1列和u2列间插值 •垂直方向： v1行和v2行间插值

双线性插值 (i)ifm (M) •第一步：水平方向线性插值 (u,v) a-2-Wfa,》+aW 2)2四 1a-号Va,fa,》+, 2-ul=1 f1=(u-4)(f(42,y)-f(4,)+f(4,y) fH2=(u-4)f(4,2)-f(4,2)月+f(4,2) fag3 hou Dianzi University杭州电子科技大学 School of Computer Science and Tecfnology计算机学院周文晖

Hangzhou Dianzi University 杭州电子科技大学 School of Computer Science and Technology 计算机学院 周文晖 双线性插值 •第一步：水平方向线性插值 u2-u1=1               1 1 21 11 11 2 1 1 2 22 12 12 2 1 ,, , ,, , H H u u f f u v f u v f u v u u u u f f u v f u v f u v u u                           1 1 21 11 11 2 1 22 12 12 ,, , ,, , H H f u u fuv fuv fuv f u u fuv fuv fuv       H1 f H 2 f

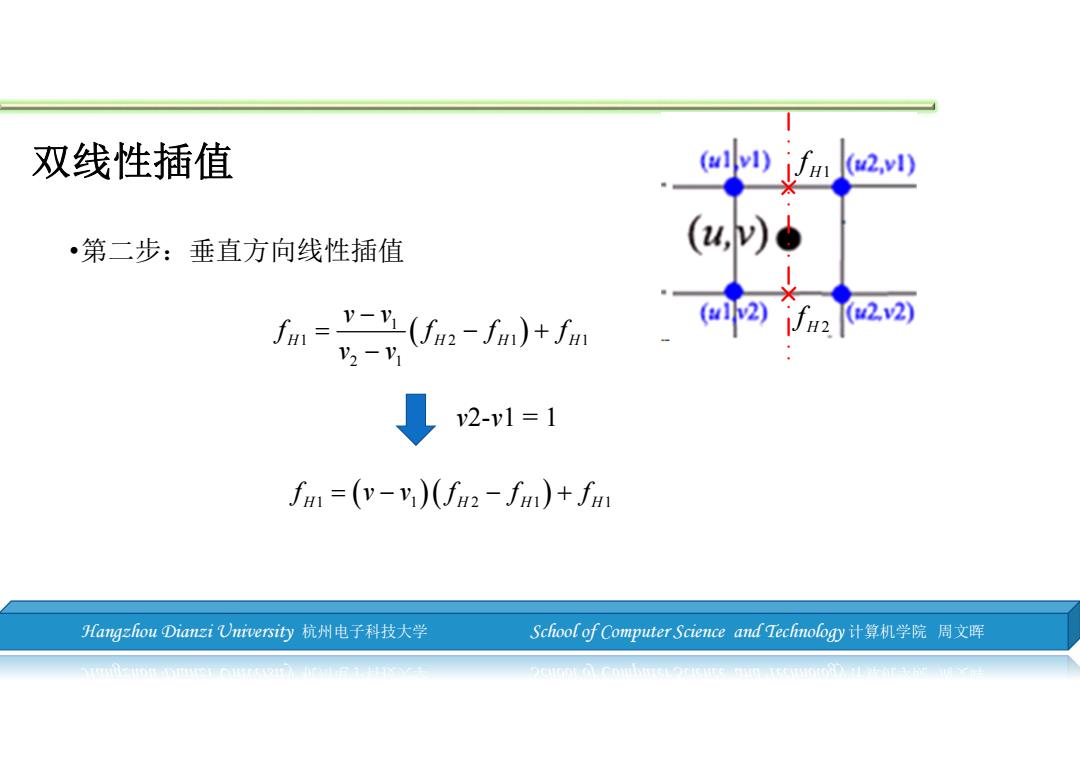
双线性插值 (if 2) •第二步：垂直方向线性插值 (,w)）b fno-fa)+fa ()() 2-vl=1 fm=(v-v)(fn2-fm)+fm Hangzhou Dianzi University杭州电子科技大学 School of Computer Science and Tecfnology计算机学院周文晖

Hangzhou Dianzi University 杭州电子科技大学 School of Computer Science and Technology 计算机学院 周文晖 双线性插值 •第二步：垂直方向线性插值 v2-v1=1   1 1 21 1 2 1 H HH H v v f ff f v v        H HH H 1 121 1 f    v v ff f H1 f H 2 f

计算空间变换 ·两个步骤： ·计算空间变换函数M ·插值填充 问题：变换矩阵未知，其参数需通过若干已知的匹配对应点后求解得到 Hangzhou Dianzi University杭州电子科技大学 School of Computer Science and Technology计算机学院周文晖

Hangzhou Dianzi University 杭州电子科技大学 School of Computer Science and Technology 计算机学院 周文晖 计算空间变换 • 两个步骤： • 计算空间变换函数 M • 插值填充 问题：变换矩阵未知，其参数需通过若干已知的匹配对应点后求解得到

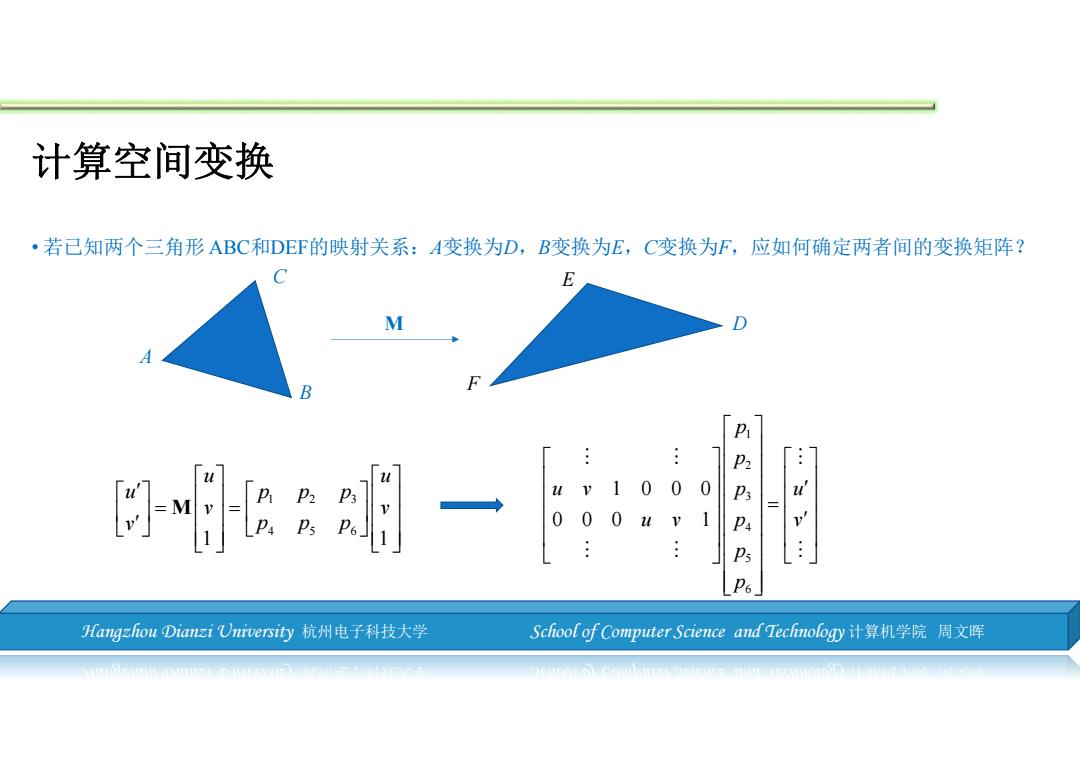
计算空间变换 ·若已知两个三角形ABC和DEF的映射关系：A变换为D,B变换为E,C变换为F,应如何确定两者间的变换矩阵？ E D B F P 7 P 0 0 0 0 0 1 .: Ps Hangzhou Dianzi University杭州电子科技大学 School of Computer Science and Tecfnology计算机学院周文晖

Hangzhou Dianzi University 杭州电子科技大学 School of Computer Science and Technology 计算机学院 周文晖 计算空间变换 • 若已知两个三角形 ABC和DEF的映射关系：A变换为D，B变换为E，C变换为F，应如何确定两者间的变换矩阵？ A B C D E F 123 456 1 1 u u u ppp v v v ppp                          M M 1 2 3 4 5 6 1000 000 1 p p uv u p uv v p p p                                            