
内古科私大拳 直接法(数值解法) 对于目标函数较为复杂或无明确的数学表达式或无法用 解析法求解的最优化问题,通常可采用直接法(数值解法)来 解决。 直接法的基本思想,就是用直接搜索方法经过一系列的 迭代以产生“点的序列(简称点列)”,使之逐步接近到最优 点。直接法常常是根据经验或试验而得到的。 非波纳奇(Fibonacci)法 区问消去法 黄金分荆法(0.618法) (-一维搜索) 函数逼近法(插值法) (2)自接法 及量轮换法 (数值解法) 爬山法 步长加速法 (多维搜索) 方向加速法 单纯形法及随机搜索法 17
17 2.直接法(数值解法) 对于目标函数较为复杂或无明确的数学表达式或无法用 解析法求解的最优化问题,通常可采用直接法(数值解法)来 解决。 直接法的基本思想,就是用直接搜索方法经过—系列的 迭代以产生“点的序列(简称点列)”,使之逐步接近到最优 点。直接法常常是根据经验或试验而得到的

窗内害古科私大举 3.以解析法为基础的数值解法。解析与数值计算相结合的方法。 4.网络最优化方法。以网络图作为数学模型,用图论方法进 行投索的寻优方法。 18
18 3.以解析法为基础的数值解法。解析与数值计算相结合的方法。 4.网络最优化方法。以网络图作为数学模型,用图论方法进 行投索的寻优方法

内喜古科私大举 ●最优控制问题基本概念 最优控制问题的描述包括: 被控系统的数学模型 目标集(“开始、终了状态”的约束条件) 容(允)许控制(u) 性能指标(从所有“容许控制”中找出一 种效果最好的控制规律);(“性能指标函数”又称 为“指标泛函”、“目标函数”、“代价函数”和 “评价函数”等) 最优控制问题的描述 19
19 ●最优控制问题基本概念 最优控制问题的描述包括: 被控系统的数学模型 目标集(“开始、终了状态”的约束条件) 容(允)许控制(u) 性能指标(从所有“容许控制”中找出一 种效果最好的控制规律);(“性能指标函数”又称 为“指标泛函” 、 “目标函数” 、 “代价函数”和 “评价函数”等) 最优控制问题的描述
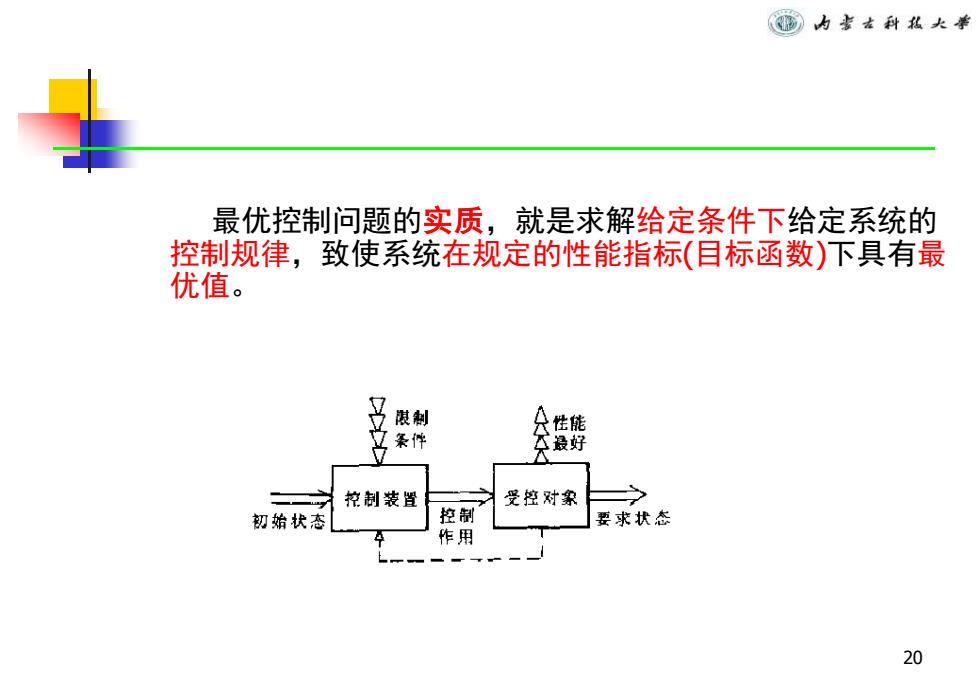
窗素古科私大拳 最优控制问题的实质,就是求解给定条件下给定系统的 控制规律,致使系统在规定的性能指标(目标函数)下具有最 优值。 限制 条件 控制装置 受控对象 初始状态 控制 要求状态 作用 20
20 最优控制问题的实质,就是求解给定条件下给定系统的 控制规律,致使系统在规定的性能指标(目标函数)下具有最 优值

内古种私大 在叙述最优控制问题的提法之前,先讨论一些基本概念。 (1)受控系统的数学模型 一个集中参数的受控系统总可以用一组一阶微分方程来描述,即状态方程,其一般形式 为: (t)=f(X(t),u(t),t) X=[x1,x2,.,xn] 是n维状态向量 u=[41,42,.,up]Y 为p维控制向量 f(X(t),u(t),t)为n维函数向量 f(X(t),u(),) f(x(t),x2(t).xn(t),4(t)42(t).4p(),t) (t0=f(X(t),u(t),)= f5(X(t),u(t),t) f3(x,(),x2(t).xn(t),4,(t),42(t).4n(t),)) : : f(X(D),u(D),1 fn(x(t),x2(t).xn(t),山1(),42()u(t),t) 21
21 在叙述最优控制问题的提法之前,先讨论一些基本概念。 (1)受控系统的数学模型 一个集中参数的受控系统总可以用一组一阶微分方程来描述,即状态方程,其一般形式 为: X(t) = f (X(t),u(t),t) T n X [x , x , , x ] = 1 2 是n维状态向量 T u u u up [ , , , ] = 1 2 为p维控制向量 f (X (t),u(t),t) 为n维函数向量 = = = ( ( ), ( ) ( ), ( ), ( ) ( ), ) ( ( ), ( ) ( ), ( ), ( ) ( ), ) ( ( ), ( ) ( ), ( ), ( ) ( ), ) ( ( ), ( ), ) ( ( ), ( ), ) ( ( ), ( ), ) ( ) ( ( ), ( ), ) 1 2 1 2 2 1 2 1 2 1 1 2 1 2 2 1 f x t x t x t u t u t u t t f x t x t x t u t u t u t t f x t x t x t u t u t u t t f X t u t t f X t u t t f X t u t t X t f X t u t t n n p n p n p n