
1.2.2货物超限等级的确定 根据超限货物定义,要判定车辆停留在水平直线上处于理想状态时,所装 货物是否超限,方法比较简单,如果货物上某一部位至车辆纵中心线所在垂直 平面的距离B(称为实测宽度)大于该部位所在高度处机车车辆限界半宽B飘时 则超限,否则不超限。 货物超限意味着与普通货物(车)相比,车辆在水平直线上处于理想状态 时,超限货物所需空间大于普通货物(车)所需空间,因而超限货物与建筑限界 间的净空小于普通货物(车)与建筑限界之间的净空,运行条件变差。车辆在水 平直线上处于理想状态时,普通货物所需空间的最大横断面尺寸为机车车辆限 界轮廓。根据货物超限程度不同,可以划分为不同的超限等级。例如在距轨面 高4000mm处,机车车辆限界半宽为1500mm,一级超限限界为1650mm,二级 超限限界为1700mm。当货物的实测宽度B>1500mm时应判为超限:当1500< B<1650mm时,为一级超限:当1650<B<1700mm时,为二级超限:B> 1700mm时为超级超限。 在半径为300m的曲线上如何判定货物是否超限呢?如果货物所需空间大 于具有机车车辆限界轮廓尺寸的普通货物(车)所需的最大空间,则该货物超 限。车辆运行到曲线上时,其纵中心线与线路中心线不在同一垂直面上,因 此,与直线上比,普通货物(车)所需的空间较大,该空间的增加量与车辆纵中 心线偏离线路中心线(所在垂直曲面)的距离(偏差量)有关,而偏差量又与车 辆长度、销距大小、曲线半径相关。判定曲线上货物是否超限采用了车长为 13.22m、销距9.35m、具有机车车辆限界轮廓尺寸的普通货车(称为计算车辆) 所需的最大空间为依据。 1.曲线上货物所需空间半宽 曲线上货物所需空间半宽是指车辆在线路上处于最不利位置时货物计算点 至线路中心线(所在垂直曲面)的距离,分为曲线内侧半宽和曲线外侧半宽。 曲线上货物所需空间半宽由三部分构成:货物半宽B(货物计算点至车辆 纵中心线所在垂直平面的距离)、货物的偏差量C(车辆转向架中心销垂直投影 在线路中心线上时车辆纵中心线偏离线路中心线的距离)、车辆转向架中心销偏 离线路中心线引起的货物的偏差量增大值g:
1.2.2 货物超限等级的确定 根据超限货物定义,要判定车辆停留在水平直线上处于理想状态时,所装 货物是否超限,方法比较简单,如果货物上某一部位至车辆纵中心线所在垂直 平面的距离 B(称为实测宽度)大于该部位所在高度处机车车辆限界半宽 B 机时 则超限,否则不超限。 货物超限意味着与普通货物(车)相比,车辆在水平直线上处于理想状态 时,超限货物所需空间大于普通货物(车)所需空间,因而超限货物与建筑限界 间的净空小于普通货物(车)与建筑限界之间的净空,运行条件变差。车辆在水 平直线上处于理想状态时,普通货物所需空间的最大横断面尺寸为机车车辆限 界轮廓。根据货物超限程度不同,可以划分为不同的超限等级。例如在距轨面 高 4000mm 处,机车车辆限界半宽为 1500mm,一级超限限界为 1650mm,二级 超限限界为 1700mm。当货物的实测宽度 B>1500mm 时应判为超限;当 1500< B≤1650mm 时,为一级超限;当 1650<B≤1700mm 时,为二级超限;B> 1700mm 时为超级超限。 在半径为 300m 的曲线上如何判定货物是否超限呢?如果货物所需空间大 于具有机车车辆限界轮廓尺寸的普通货物(车)所需的最大空间,则该货物超 限。车辆运行到曲线上时,其纵中心线与线路中心线不在同一垂直面上,因 此,与直线上比,普通货物(车)所需的空间较大,该空间的增加量与车辆纵中 心线偏离线路中心线(所在垂直曲面)的距离(偏差量)有关,而偏差量又与车 辆长度、销距大小、曲线半径相关。判定曲线上货物是否超限采用了车长为 13.22m、销距 9.35m、具有机车车辆限界轮廓尺寸的普通货车(称为计算车辆) 所需的最大空间为依据。 1. 曲线上货物所需空间半宽 曲线上货物所需空间半宽是指车辆在线路上处于最不利位置时货物计算点 至线路中心线(所在垂直曲面)的距离,分为曲线内侧半宽和曲线外侧半宽。 曲线上货物所需空间半宽由三部分构成:货物半宽 B(货物计算点至车辆 纵中心线所在垂直平面的距离)、货物的偏差量 C(车辆转向架中心销垂直投影 在线路中心线上时车辆纵中心线偏离线路中心线的距离)、车辆转向架中心销偏 离线路中心线引起的货物的偏差量增大值 g

1)用一辆六轴及以下货车装载时货物所需空间半宽 (1)货物的偏差量 如图1一1一12所示,车上装有货物一件,当车辆运行在曲线上,两转向架 中心销M、N恰好垂直投影在线路中心线上时,车辆纵中心线与线路中心线相 割。车辆纵中心线在从、N之间向线路中心线内侧偏离,产生内偏差量:在 M、外方,向线路中心线外侧偏离,产生外偏差量。车上所装货物也随车辆 一起产生内或外偏差量。欲知车上所装货物是否超限或其超限等级,必须知道 A、D所在横断面处的车辆纵中心线的偏差量C内=PP和C外=TT 0 图1一1一12货物内外偏差量示意图 在图1一1一12中,MN为车辆的销距,用1表示。G为车辆纵、横中心线的 交点,P?平行于车辆纵中心线、与车辆横中心线相交于F,因而 C=PP=KG-KF 半径为R的曲线线路中心线是直径为2R圆的圆周的一部分。如果在图上把 这个圆补画全了,车辆销距1为一个弦,将KG延长到与圆周相交,则又是一个 弦,这个弦必然通过圆心,弦长为2R。根据相交弦定理,有 KG2R-KG)=令 (1/2)2 KG-2R-KG) 分母中KG《2R,可略而不计,所以 12 KG=8R PQ是圆的另一个弦(弦长为2x)与直径相交于F,同理可得
1)用一辆六轴及以下货车装载时货物所需空间半宽 (1)货物的偏差量 如图 1-1-12 所示,车上装有货物一件,当车辆运行在曲线上,两转向架 中心销 M、N 恰好垂直投影在线路中心线上时,车辆纵中心线与线路中心线相 割。车辆纵中心线在 M、N 之间向线路中心线内侧偏离,产生内偏差量;在 M、N 外方,向线路中心线外侧偏离,产生外偏差量。车上所装货物也随车辆 一起产生内或外偏差量。欲知车上所装货物是否超限或其超限等级,必须知道 A、D 所在横断面处的车辆纵中心线的偏差量 C 内=PP′和 C 外=TT′。 D x x B2 C外 T' T N K Q F G H P P' M A 图 1-1-12 货物内外偏差量示意图 在图 1-1-12 中,MN 为车辆的销距,用 l 表示。G 为车辆纵、横中心线的 交点,P′Q 平行于车辆纵中心线、与车辆横中心线相交于 F,因而 C 内=PP′=KG-KF 半径为R的曲线线路中心线是直径为2R圆的圆周的一部分。如果在图上把 这个圆补画全了,车辆销距 l 为一个弦,将 KG 延长到与圆周相交,则又是一个 弦,这个弦必然通过圆心,弦长为 2R。根据相交弦定理,有 2 ) 2 (2 ) ( l KG R KG (2 ) ( / 2) 2 R KG l KG 分母中 KG《2R,可略而不计,所以 R l KG 8 2 P′Q 是圆的另一个弦(弦长为 2x)与直径相交于 F,同理可得

KF=(2x) 8R 由此可得内偏差量的计算公式,并将计算结果的单位转换为毫米 c-P-x100m) 8R (1-1-1) 式中一车辆销距,m: 一车辆横中心线至货物计算点所在横断面(简称检定断面)的距离, m: R—曲线半径,m。 D点所在横断面在车辆转向架中心销外方,在这个断面上,车辆纵中心线 的偏差量 C#=TT=KH一G 根据相交弦定理 KI 由此可得外偏差量的计算公式,并将计算结果的单位转换为毫米 C4=2x-1x100mm (1-1-2) 式中x一车辆横中心线至货物检定断面的距离,m。 对于非等断面体货物,应根据货物具体外形、突出部分的位置以及所用车 辆综合考虑。多数情况下需要通过计算不同断面处的偏差量进行综合比较才可 确定货物的超限等级。 (2)车辆转向架中心销偏离线路中心线引起的货物偏差量增大值 ①车底架上心盘中心偏离线路中心线的最大值 车辆转向架各组成部分之间存在游间(旷量),钢轨内侧与轮缘外侧存在 游间,以及由于车轮踏面的锥度导致转向架在钢轨上的蛇行,使得车底架上心 盘中心一般情况下偏离线路中心线。 以上原因使车底架上心盘中心向线路中心线一侧的最大可能偏移量 e=75mm
R x KF 8 (2 ) 2 由此可得内偏差量的计算公式,并将计算结果的单位转换为毫米 1000 8 (2 ) 2 2 R l x C内 (mm) (1-1-1) 式中 l——车辆销距,m; x——车辆横中心线至货物计算点所在横断面(简称检定断面)的距离, m; R——曲线半径,m。 D 点所在横断面在车辆转向架中心销外方,在这个断面上,车辆纵中心线 的偏差量 C 外=TT′=KH-KG 根据相交弦定理 R x KH 8 (2 ) 2 由此可得外偏差量的计算公式,并将计算结果的单位转换为毫米 1000 8 (2 ) 2 2 R x l C外 (mm) (1-1-2) 式中 x——车辆横中心线至货物检定断面的距离,m。 对于非等断面体货物,应根据货物具体外形、突出部分的位置以及所用车 辆综合考虑。多数情况下需要通过计算不同断面处的偏差量进行综合比较才可 确定货物的超限等级。 (2)车辆转向架中心销偏离线路中心线引起的货物偏差量增大值 ① 车底架上心盘中心偏离线路中心线的最大值 车辆转向架各组成部分之间存在游间(旷量),钢轨内侧与轮缘外侧存在 游间,以及由于车轮踏面的锥度导致转向架在钢轨上的蛇行,使得车底架上心 盘中心一般情况下偏离线路中心线。 以上原因使车底架上心盘中心向线路中心线一侧的最大可能偏移量 e=75mm
②货物计算点位于车辆转向架中心销之间时,转向架中心销偏离线路中 心线引起的货物偏差量增大值 货物计算点位于车辆转向架中心销之间,当车辆两转向架中心销M、N同 时向曲线线路中心线内侧偏移且达到最大值时,由转向架中心销偏离线路中 心线引起的货物偏差量增大值达到最大,如图1一1一13所示,其值为 g=e=75mm 车辆纵中心线 一车辆纵中心线 线路中心线 图1一1一13车辆两转向架中心销同时向曲线线路中心线内侧偏移示意图 ③货物计算点位于车辆转向架中心销外方时,转向架中心销偏离线路中 心线引起的货物偏差量增大值 货物计算点位于车辆转向架中心销外方,当车辆两转向架中心销M、N分 别向曲线线路中心线两侧偏移且均达到最大值时,由转向架中心销偏离线路 中心线引起的货物偏差量增大值达到最大,如图1一1一14所示,其值为 车辆纵中心线 、]C,车辆纵中心线 线路中心线 图1一1一14车辆两转向架中心销同时向曲线线路中心线两侧偏移示意图 (3)曲线上货物所需空间半宽 由前可知,曲线上货物所需空间半宽B=B十C十g。因此, 曲线上货物所需空间内侧半宽 B南=B+C6+g=B+-2x1000+75mm 8R
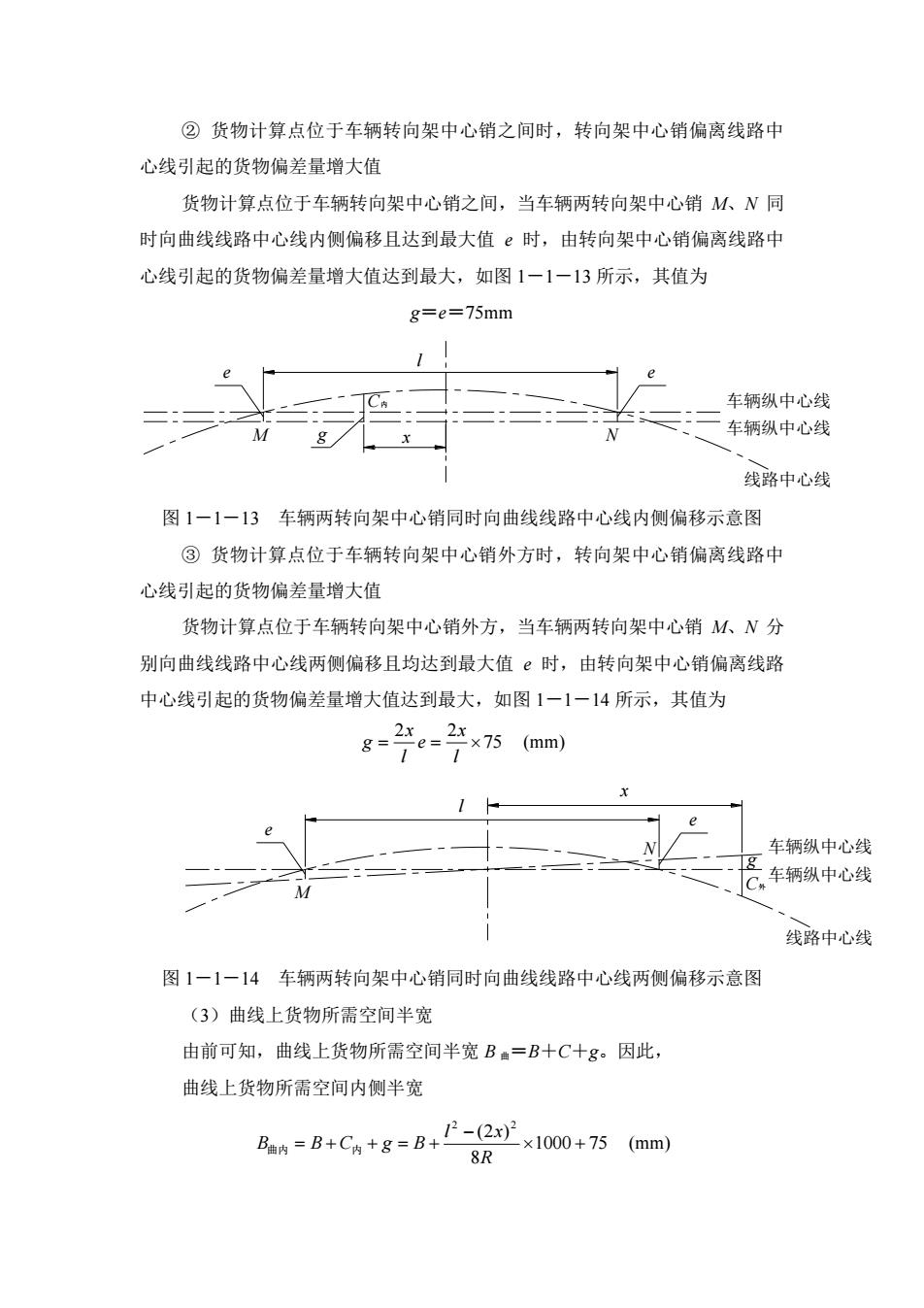
② 货物计算点位于车辆转向架中心销之间时,转向架中心销偏离线路中 心线引起的货物偏差量增大值 货物计算点位于车辆转向架中心销之间,当车辆两转向架中心销 M、N 同 时向曲线线路中心线内侧偏移且达到最大值 e 时,由转向架中心销偏离线路中 心线引起的货物偏差量增大值达到最大,如图 1-1-13 所示,其值为 g=e=75mm M N e e 线路中心线 车辆纵中心线 车辆纵中心线 l x C内 g 图 1-1-13 车辆两转向架中心销同时向曲线线路中心线内侧偏移示意图 ③ 货物计算点位于车辆转向架中心销外方时,转向架中心销偏离线路中 心线引起的货物偏差量增大值 货物计算点位于车辆转向架中心销外方,当车辆两转向架中心销 M、N 分 别向曲线线路中心线两侧偏移且均达到最大值 e 时,由转向架中心销偏离线路 中心线引起的货物偏差量增大值达到最大,如图 1-1-14 所示,其值为 75 2 2 l x e l x g (mm) M N e e 线路中心线 车辆纵中心线 车辆纵中心线 l g C外 x 图 1-1-14 车辆两转向架中心销同时向曲线线路中心线两侧偏移示意图 (3)曲线上货物所需空间半宽 由前可知,曲线上货物所需空间半宽 B 曲=B+C+g。因此, 曲线上货物所需空间内侧半宽 1000 75 8 (2 ) 2 2 R l x B曲内 B C内 g B (mm)

曲线上货物所需空间外侧半宽 Bw=B+C4+g=B+2-1x100+2×75m 8R 2)用普通平车跨装时货物所需空间半宽 采用两车跨装时,跨装车组中两辆负重的普通平车运行到曲线上的情形如 图1一1一15所示,m、n分别表示两负重车转向架中心销,1为销距:P、Q分别 表示两个货物转向架中心销(亦即两负重车中央),设两负重车的车型相同,两 R:PQ为跨装支距,用 12 货物转向架中心销偏离线路中心线的距离MP=NQ= L表示:KU平行于PQ。 H 图1一1一15跨装货物偏差量示意图 (1)货物计算点位于两货物转向架中心销内方时 距跨装支距横中心线距离为x的断面处,跨装货物的内偏差量为SS',SS =EF+EG, 发时 12 EG=KP-MP= 8R 故货物的内偏差量 C2x100 (mm) (1-1-3) 8R 式中L跨装支距,m: —负重车销距,m 检定断面至跨装支距横中心线的距离,m
曲线上货物所需空间外侧半宽 75 2 1000 8 (2 ) 2 2 l x R x l B曲外 B C外 g B (mm) 2)用普通平车跨装时货物所需空间半宽 采用两车跨装时,跨装车组中两辆负重的普通平车运行到曲线上的情形如 图1-1-15所示,m、n分别表示两负重车转向架中心销,l为销距;P、Q分别 表示两个货物转向架中心销(亦即两负重车中央),设两负重车的车型相同,两 货物转向架中心销偏离线路中心线的距离 R l MP NQ 8 2 ;PQ 为跨装支距,用 L 表示;KU 平行于 PQ。 S x U n n m m E l D x T' N T Q K F G H P S' M 图 1-1-15 跨装货物偏差量示意图 (1)货物计算点位于两货物转向架中心销内方时 距跨装支距横中心线距离为 x 的断面处,跨装货物的内偏差量为 SS′,SS′ =EF+EG, R x R L EF 8 (2 ) 8 2 2 EG=KP≈MP= R l 8 2 故货物的内偏差量 1000 8 (2 ) 2 2 2 R L l x C内 (mm) (1-1-3) 式中 L——跨装支距,m; l——负重车销距,m; x——检定断面至跨装支距横中心线的距离,m