
4.1分布式路由算法导论: 四、路由函数 ·路由函数定义一个消息如何从源节点路由到目标节点 每个PE在收到一个消息以后,都将决定: 1)把这条消息传送到本地存储器,还是 2)转发到一个邻接的PE ·有许多不同的路由函数的定义,例如 依赖于目标的、依赖于输入的、依赖于源的、依赖于路径的 等等 仅仅依赖于当前依赖于依濑赖于目标节点和从源节点到当前节点的路径 一 般而言,路田函效参写的后忌必多,双未可驼机必灯 ·本章仅使用依赖于目标的路由函数 2008.3.28 Advanced Operating System 17/91
2008.3.28 Advanced Operating System 17/91 4.1分布式路由算法导论: 四、路由函数 ⚫ 路由函数定义一个消息如何从源节点路由到目标节点 ⚫ 每个PE在收到一个消息以后,都将决定: 1)把这条消息传送到本地存储器,还是 2)转发到一个邻接的PE ⚫ 有许多不同的路由函数的定义,例如 ⚫ 依赖于目标的、依赖于输入的、依赖于源的、依赖于路径的 等等 ⚫ 一般而言,路由函数参考的信息越多,效果可能就越好 ⚫ 本章仅使用依赖于目标的路由函数 仅仅依赖于当前和目标节点 依赖于当前、目标节点,以及输入的邻接节点 依赖于目标节点和从源节点到当前节点的路径 依赖于源、当前、目标节点

4.2一般类型网络的最短路径路由算法 许多分组交换网,如法国的Transpac或美国 的ARPAnet都使用最短路径路由 三个一般类型网络的最短路径路由算法: 1.Dijkstra集中式算法 2.Ford分布式算法 3.ARPAnetI路由算法 2008.3.28 Advanced Operating System 18/91
2008.3.28 Advanced Operating System 18/91 4.2 一般类型网络的最短路径路由算法 ⚫ 许多分组交换网,如法国的Transpac或美国 的ARPAnet都使用最短路径路由 ⚫ 三个一般类型网络的最短路径路由算法: 1. Dijkstra集中式算法 2. Ford分布式算法 3. ARPAnet路由算法
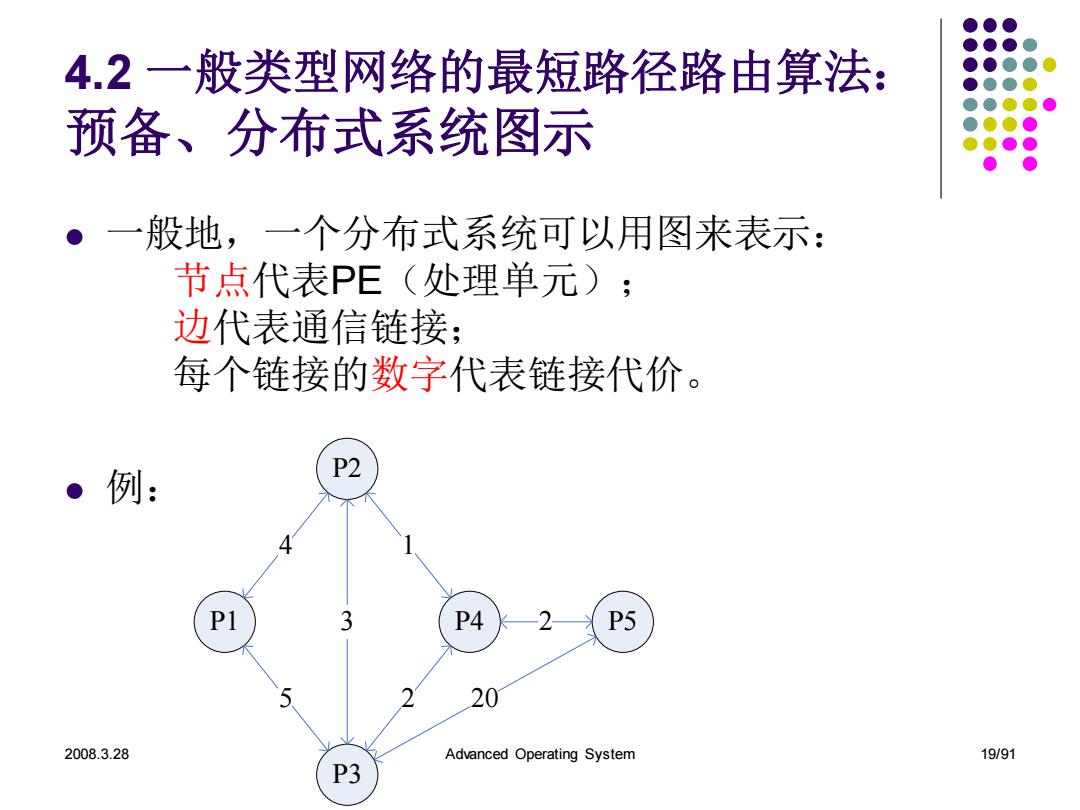
4.2一般类型网络的最短路径路由算法: 预备、分布式系统图示 。一 般地,一个分布式系统可以用图来表示: 节点代表PE(处理单元); 边代表通信链接; 每个链接的数字代表链接代价。 ·例: P2 4 P1 3 P4 2 P5 2 20 2008.3.28 Advanced Operating System 19/91 P3
2008.3.28 Advanced Operating System 19/91 4.2 一般类型网络的最短路径路由算法: 预备、分布式系统图示 ⚫ 一般地,一个分布式系统可以用图来表示: 节点代表PE(处理单元); 边代表通信链接; 每个链接的数字代表链接代价。 ⚫ 例: P1 P2 P3 P4 P5 4 5 3 1 2 2 20

4.2.1 Dijkstra集中式算法 ●第一种类型的算法以集中式的风格进行路由 ·Dijkstra集中式算法可以发现一个源节点到所 有其他节点的最短路径。算法需求: 需要了解给定网络的全局拓扑消息,即: 1、网络中所有其它节点的列表; 2、节点之间的所有链接; 3、每个链接的代价。 2008.3.28 Advanced Operating System 20/91
2008.3.28 Advanced Operating System 20/91 4.2.1 Dijkstra集中式算法 ⚫ 第一种类型的算法以集中式的风格进行路由 ⚫ Dijkstra集中式算法可以发现一个源节点到所 有其他节点的最短路径。算法需求: ⚫ 需要了解给定网络的全局拓扑消息,即: 1、网络中所有其它节点的列表; 2、节点之间的所有链接; 3、每个链接的代价

4.2.1 Dijkstra集中式算法: 一、 算法描述 设 D(W)是从源s到节点V的距离(沿给定路径的链接的代价的 和) I(V,w)是节点v和w之间的代价 Dijkstra算法如下: 1. 设N={s: 对不在N中的每一个节点V,令D(=(s,V)。 即与$相邻的节点 对那些没有连接到s的节点赋值为∞。 2. 找到不在N中的一个节点W,使D(W最小并将w加入N: 然后对所有不在N中的其它节点计算并更新D(): D(v):min[D(V),D(w)+I(w,v)] 重复步骤2,直到所有节点都在N中 D(w) ×2 N 2008.3.28 Advanced Operating System 21/91 D()
2008.3.28 Advanced Operating System 21/91 设 D(v)是从源s到节点v的距离(沿给定路径的链接的代价的 和) l(v,w)是节点v和w之间的代价 Dijkstra算法如下: 1. 设N={s}; 对不在N中的每一个节点v,令D(v)=l(s,v)。 对那些没有连接到s的节点赋值为∞。 2. 找到不在N中的一个节点w,使D(w)最小并将w加入N; 然后对所有不在N中的其它节点计算并更新D(v): D(v) := min[D(v), D(w)+l(w,v)] 重复步骤2,直到所有节点都在N中 N 4.2.1 Dijkstra集中式算法: 一、算法描述 s v w D(v) D(w) ? N 即与s相邻的节点