
第七章图 学习要点 理解图的基本概念及有关术语,掌握图的四种存储 结构的表示方法; 熟练掌握图的两种遍历(深度优先搜索和广度优先 搜索),能列出按上述两种遍历算法得到的序列; 理解最小生成树的概念,能按Prim算法构造最小生 成树; 掌握求最短路径、拓扑排序以及关键路径的算法思 想
第七章 图 ◼ 理解图的基本概念及有关术语,掌握图的四种存储 结构的表示方法; ◼ 熟练掌握图的两种遍历(深度优先搜索和广度优先 搜索),能列出按上述两种遍历算法得到的序列; ◼ 理解最小生成树的概念,能按Prim算法构造最小生 成树; ◼ 掌握求最短路径、拓扑排序以及关键路径的算法思 想。 学习要点

7.1图的的定义和术语 必图的定义 图是由一个顶点集V和一个描述顶点之间关系 (边或者弧)的集合VR构成的数据结构。 Graph (V,VR) 其中,VR={<V,wPIV,w∈V且P(y,w)} <V,w>表示从v到w的一条弧,并称V为弧尾或 初始点,W为弧头或终端点。 谓词P(N,w)定义了弧<V,w>的意义或信息
7.1 图的的定义和术语 图是由一个顶点集 V和一个描述顶点之间关系 (边或者弧)的集合VR构成的数据结构。 Graph = ( V , VR ) 其中,VR={<v,w>| v,w∈V 且 P(v,w)} <v,w>表示从 v 到 w 的一条弧,并称 v 为弧尾或 初始点,w 为弧头或终端点。 谓词 P(v,w) 定义了弧 <v,w>的意义或信息。 ❖ 图的定义
公图的应用举例 例1交通图(公路、铁路) 顶点:地点 边:连接地点的公路 例2电路图 顶点:元件 边:连接元件之间的线路 例3各种流程图 如产品的生产流程图 /3 顶点:工序 边:各道工序之间的顺序关系
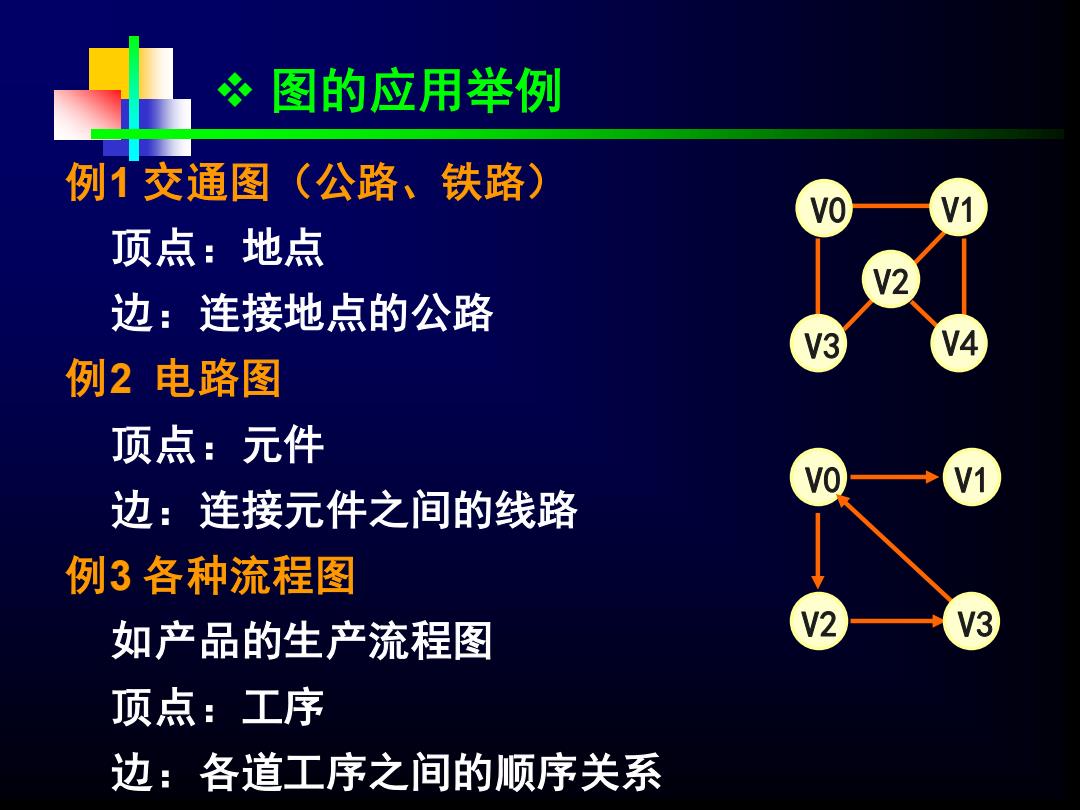
❖ 图的应用举例 例1 交通图(公路、铁路) 顶点:地点 边:连接地点的公路 例2 电路图 顶点:元件 边:连接元件之间的线路 例3 各种流程图 如产品的生产流程图 顶点:工序 边:各道工序之间的顺序关系 V0 V3 V4 V1 V2 V0 V2 V3 V1

冬有向图和无向图 在图中,若用箭头标明了边是有方向性的,则称这 样的图为有向图,否则称为无向图。 在无向图中,一条边(x,y)与(y,x)表示的结果 相同,用圆括号表示。例如: G1=<V1,E1> V1={v0,V1,v2,v3,V4} E1={N0,V1),(0,v3),(y1,V2),(V1,V4),(v2,V3),(V2,v4)}
❖ 有向图和无向图 G1=<V1, E1> V1={v0, v1, v2, v3, v4 } E1={(v0,v1),(v0,v3),(v1,v2),(v1,v4),(v2,v3),(v2,v4)} V0 V3 V4 V1 V2 在图中,若用箭头标明了边是有方向性的,则称这 样的图为有向图,否则称为无向图。 在无向图中,一条边(x,y)与(y,x)表示的结果 相同,用圆括号表示。例如:

冬有向图和无向图 在有向图中,一条边<x,y>与sy,x>表示的结果不 相同,用尖括号表示。<x,y>表示从顶点出发向顶 点y的边,x为始点,y为终点。例如: G2=<V2,A2> V2=v0,v1,v2,v3} A2={v0,V1>,<v0,V2>,<v2,V3>,<v3,v0>}
在有向图中,一条边<x,y>与<y,x>表示的结果不 相同,用尖括号表示。<x,y>表示从顶点x出发向顶 点y的边,x为始点,y为终点。例如: G2=<V2, A2> V2={v0, v1, v2, v3} A2={<v0,v1 >, <v0,v2 >, <v2,v3 >, <v3,v0 >} V0 V2 V3 V1 ❖ 有向图和无向图