
”名词和术语 顶点、边、弧、弧头、弧尾 完全图、稠密图、稀疏图 度、入度、出度 边的权、网图 路径、路径长度 回路、简单路径、简单回路 子图 连通图、连通分量 强连通图、强连通分量 生成树、生成森林
❖ 名词和术语 顶点、边、弧、弧头、弧尾 完全图、稠密图、稀疏图 度、入度、出度 边的权、网图 路径、路径长度 回路、简单路径、简单回路 子图 连通图、连通分量 强连通图、强连通分量 生成树、生成森林
·顶点、边、弧、弧头、弧尾 图中的数据元素通常称为顶点; 若<y,w>∈VR,则<V,w>表示从v到w的一条弧,且 称V为弧尾或初始点,称w为弧头或终端点。 若<V,w>∈VR,必有则sw,V>∈VR,即VR是对称 的,则以无序对(,w)代替这两个有序对,表示从V和 w的一条边。 W
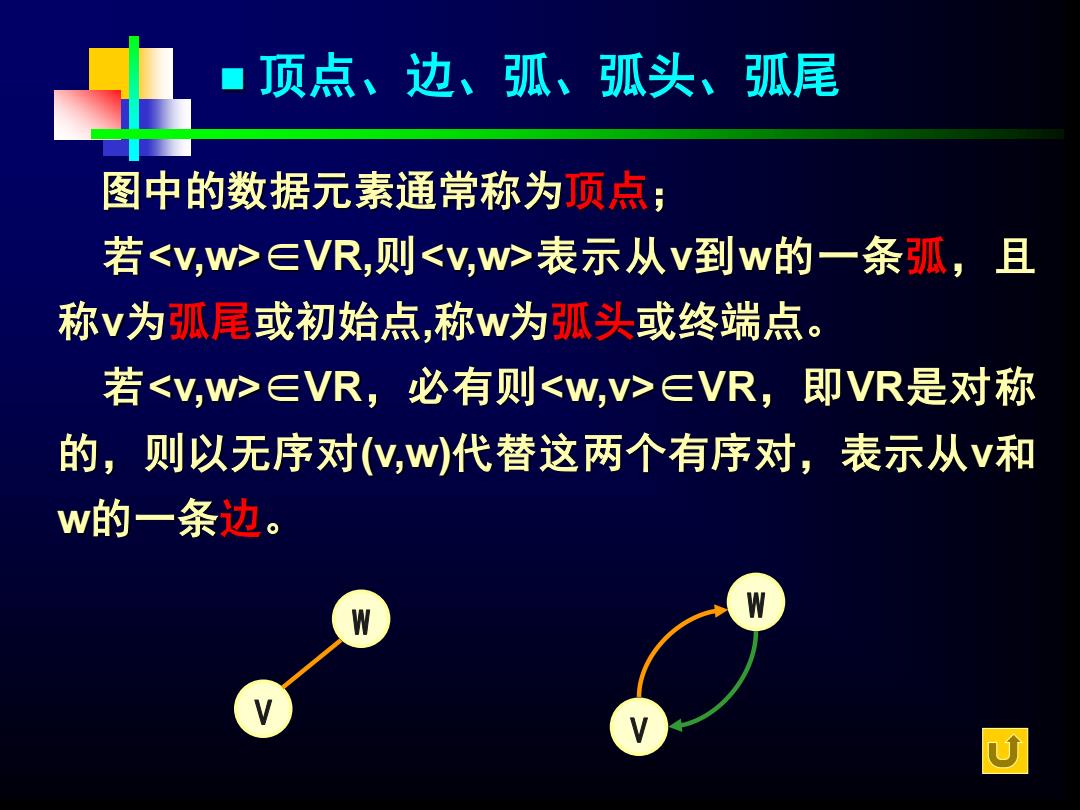
◼ 顶点、边、弧、弧头、弧尾 V W V W 图中的数据元素通常称为顶点; 若<v,w>∈VR,则<v,w>表示从v到w的一条弧,且 称v为弧尾或初始点,称w为弧头或终端点。 若<v,w>∈VR,必有则<w,v>∈VR,即VR是对称 的,则以无序对(v,w)代替这两个有序对,表示从v和 w的一条边
·完全图、稠密图、稀疏图 在一个无向图中,如果任意两顶点都有一条直接边 相连接,则称该图为无向完全图。 在一个有向图中,如果任意两顶点之间都有方向互 为相反的两条弧相连接,则称为有向完全图 若一个图接近完全图,称为稠密图; 称边数很少的 图为稀疏图 无向完全图 有向完全图
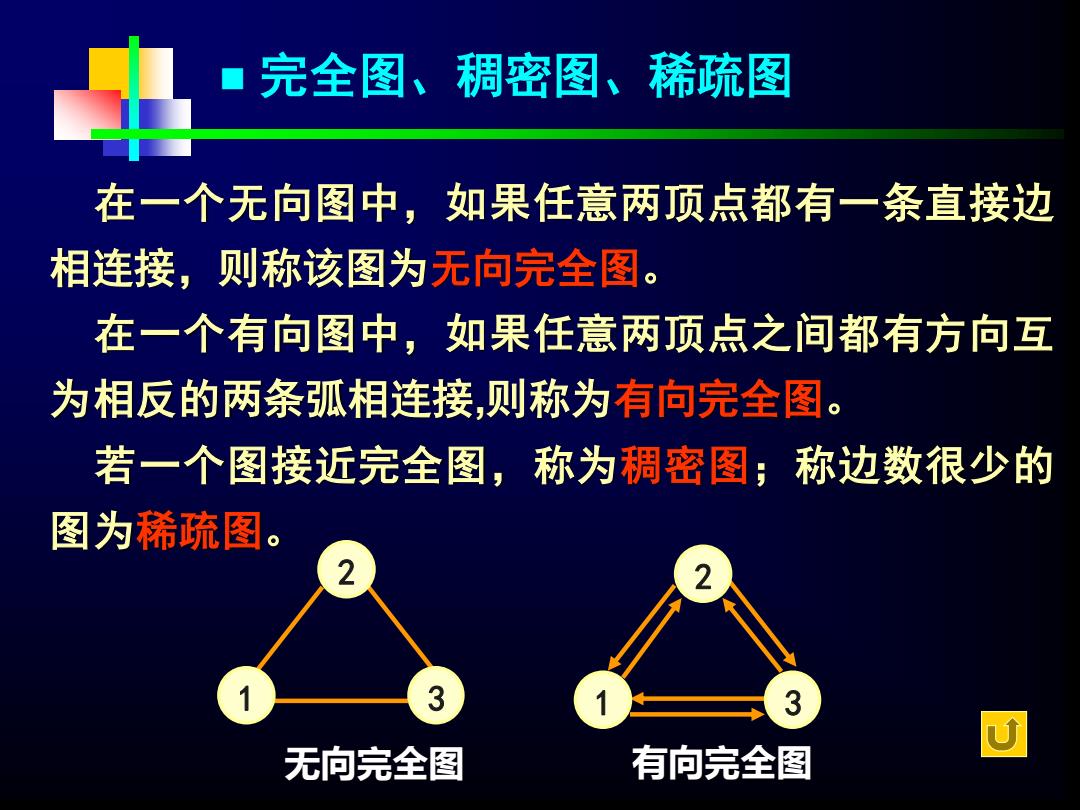
在一个无向图中,如果任意两顶点都有一条直接边 相连接,则称该图为无向完全图。 在一个有向图中,如果任意两顶点之间都有方向互 为相反的两条弧相连接,则称为有向完全图。 若一个图接近完全图,称为稠密图;称边数很少的 图为稀疏图。 无向完全图 有向完全图 1 3 2 1 3 2 ◼ 完全图、稠密图、稀疏图
度、入度、出度 在图中,一个顶点依附的边或弧的数目,称为该顶 点的度。在有向图中,以顶点V为起点的有向边数称 为顶点V的出度,以顶点V为终点的有向边数称为顶点 V的入度,入度和出度之和称为该顶点的度。 5 5 3
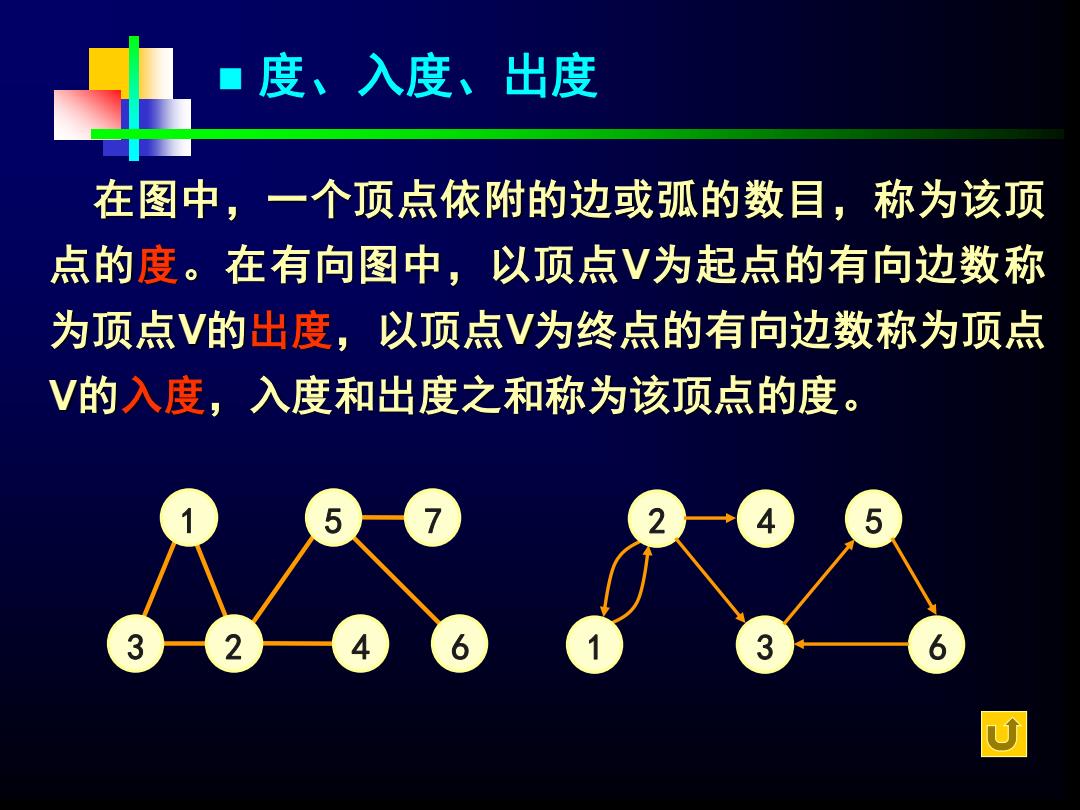
1 7 2 6 5 3 4 2 5 3 6 4 1 ◼ 度、入度、出度 在图中,一个顶点依附的边或弧的数目,称为该顶 点的度。在有向图中,以顶点V为起点的有向边数称 为顶点V的出度,以顶点V为终点的有向边数称为顶点 V的入度,入度和出度之和称为该顶点的度
·边的权、网 与边有关的数据信息称为权。 边上带权的图称为网。 2 3 A B 4 5 (a)无向网 (b)有向网 回
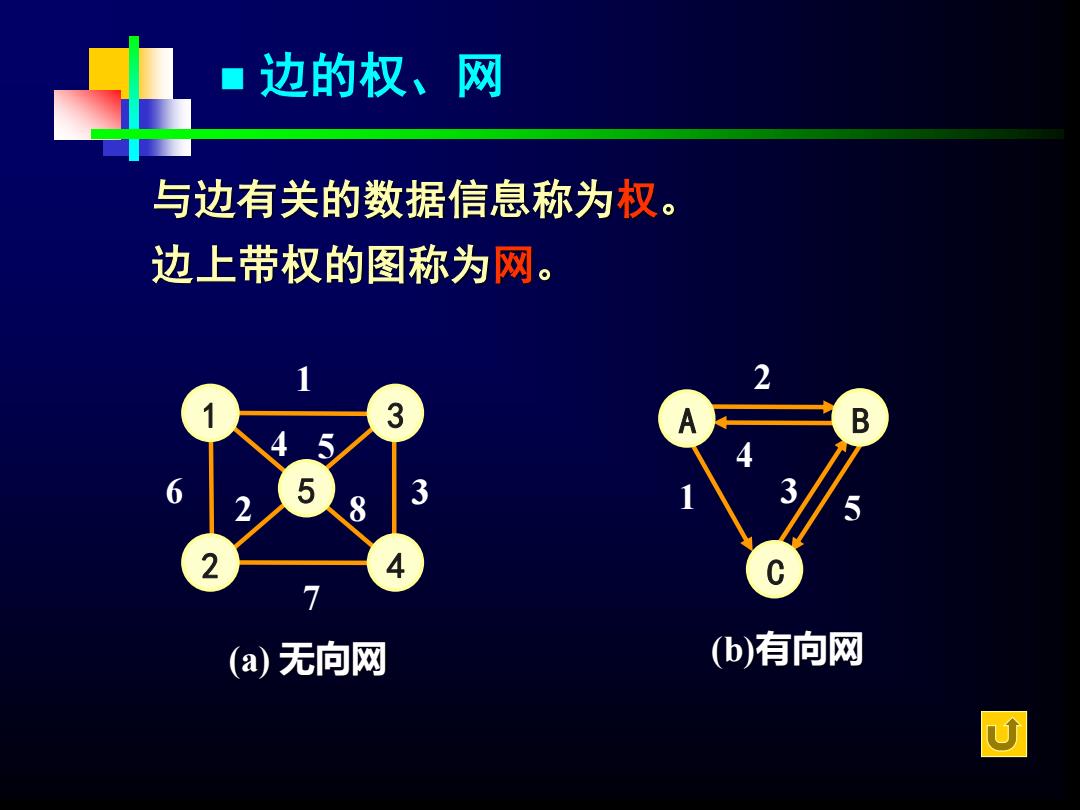
◼ 边的权、网 1 2 5 4 3 1 7 6 3 2 4 5 8 B C A 2 1 4 3 5 (a) 无向网 (b)有向网 与边有关的数据信息称为权。 边上带权的图称为网