
序列蜜码 主讲人:马春光 machunguang@hrbeu.edu.cn CNR@HEU http://machunguang.hrbeu.edu.cn
序列密码 主讲人:马春光 machunguang@hrbeu.edu.cn

本讲主要内容 。序列密码的介绍 。线性反馈移位寄存器 。非线性序列 。序列密码的算法举例(A5、RC4) CNR@HEU http://machunguang.hrbeu.edu.cn
本讲主要内容 序列密码的介绍 线性反馈移位寄存器 非线性序列 序列密码的算法举例(A5、RC4) 3

序列密码的简介 序列密码通常认为起源于20世纪20年代的维尔姆(ernam) 密码,Vernam密码中的密钥序列要求是随机的序列,由于随机 的密钥序列的产生、存储以及分配等方面存在一定的困难, Vernam体制在当时并没有得到广泛的应用。随着微电子技术和 数学理论的发展和完善,基于伪随机序列的序列密码得到了长 足的发展和应用,其产生有比较成熟的数学理论工具。如果密 钥序列是随机的序列,则序列密码就是“一次一密”密码体制。 商农已经证明“一次一密”密码体制在理论上是不可破译的。 目前,序列密码是世界各国的军事和外交等重要领域中使用的 主要密码体制之一。 在序列密码中,加密和解密所用的密钥序列都是伪随机序 列,序列密码是对称密码体制中的一类,又称为流密码。 CNR@HEU http://machunguang.hrbeu.edu.cn
序列密码的简介 序列密码通常认为起源于 序列密码通常认为起源于20世纪20年代的维尔姆(Vernam) 密码,Vernam密码中的密钥序列要求是随机的序列,由于 密码中的密钥序列要求是随机的序列,由于随机 的密钥序列的产生、存储以及分配等方面存在一定的困难, Vernam体制在当时并没有得到广泛的应用。随着微电子技术和 体制在当时并没有得到广泛的应用。随着微电子技术和 数学理论的发展和完善,基于伪随机序列的序列密码得到了长 足的发展和应用,其产生有比较成熟的数学理论工具。如果密 钥序列是随机的序列,则序列密码就是“一次一密”密码体制。 商农已经证明“一次一密”密码体制在理论上是不可破译的。 目前,序列密码是世界各国的军事和外交等重要领域中使用的 主要密码体制之一。 在序列密码中,加密和解密所用的密钥序列都是伪随机序 列,序列密码是对称密码体制中的一类,又称为流密码。 4 列,序列密码是对称密码体制中的一类,又称为流密码

序列密码的描述 在序列密码中,将明文消息按一定长度(长度较小)分 组,然后对各组用相关但不同的密钥进行加密,产生相应的 密文,相同的明文分组会因在明文序列中的位置不同而对应 于不同的密文分组。解密用相同的密钥序列对密文序列进行 分组解密以恢复出明文序列。 >设明文为p=poPP2… P,∈GF(2,20 >设密钥为k=k,kk2… k,∈GF2),20 >设密文为C=CoC1C2… y,∈GF2),20 >则加密变换为c,=EkP) ≥0 >则解密变换为p,=Dkc) 20 CNR@HEU http://machunguang.hrbeu.edu.cn
序列密码的描述 在序列密码中,将明文消息按一定长度 将明文消息按一定长度 将明文消息按一定长度 将明文消息按一定长度(长度较小)分 组,然后对各组用相关但不同的密钥进行加密,产生相应的 密文,相同的明文分组会因在明文序列中的位置不同而对应 于不同的密文分组。解密用相同的密钥序列对密文序列进行 分组解密以恢复出明文序列。 ¾设明文为p=p0p1p2… … pi∈GF(2), i≥0 ¾设密钥为k=k0k1k2… … ki∈GF(2), i≥0 ¾设密文为c c= 0c1c2… yi∈GF(2), i≥0 ¾则加密变换为ci=Eki(pi) i≥0 ¾则解密变换为p D (c ) i≥0 5 ¾则解密变换为pi=Dki(ci) i≥0
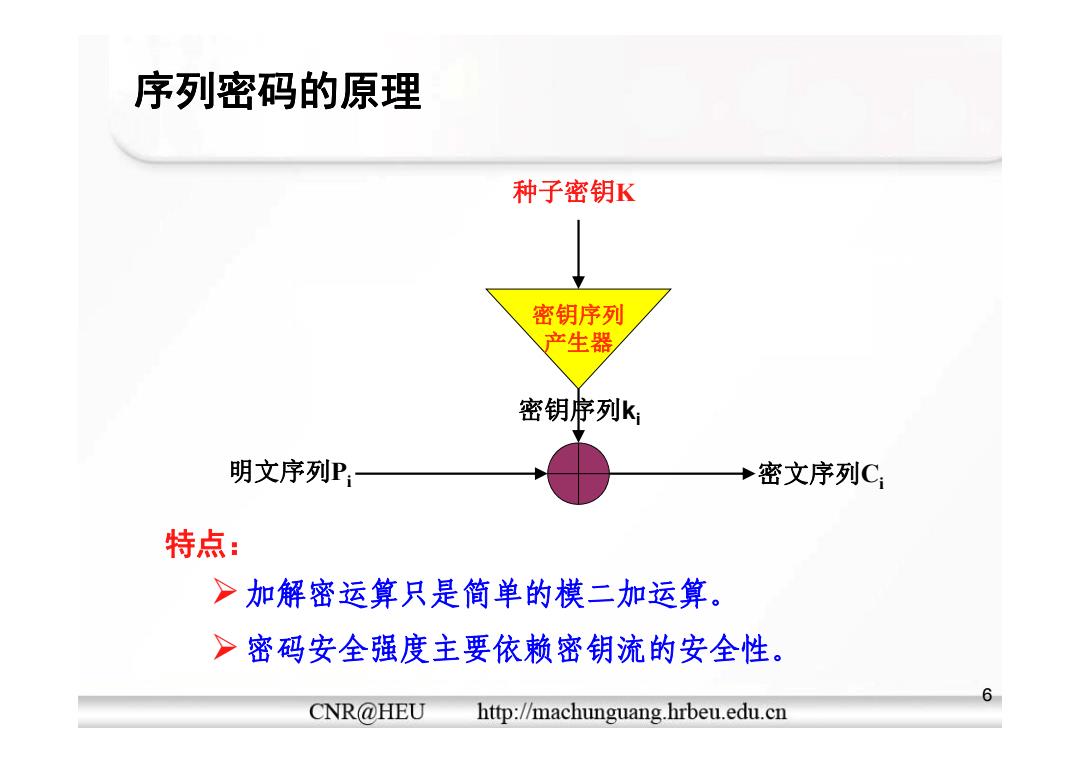
序列密码的原理 种子密钥K 密钥序列 产生器 密钥序列k: 明文序列P +密文序列C 特点: >加解密运算只是简单的模二加运算。 >密码安全强度主要依赖密钥流的安全性。 6 CNR@HEU http://machunguang.hrbeu.edu.cn
序列密码的原理 种子密钥K 密钥序列 产生器 明文序列P 密文序列C 密钥序列ki 明文序列Pi 密文序列Ci 特点: ¾ 加解密运算只是简单的模二加运算。 ¾ 密码安全强度主要依赖密钥流的安全性。 特点: 6 ¾ 密码安全强度主要依赖密钥流的安全性