
匹配和最大匹配 ■贝尔热定理:对于图G=<V,E>和匹配M二E,M是最大匹配当 且仅当G不含M增广路。 ■充分性:采用反证法,假设最大匹配M|>M 2023/4/3 26
n 贝尔热定理:对于图G = <V, E>和匹配M ⊆ E,M是最大匹配当 且仅当G不含M增广路。 n 充分性:采用反证法,假设最大匹配|M’| > |M| 2023/4/3 26 匹配和最大匹配

匹配和最大匹配 ■贝尔热定理:对于图G=<V,E>和匹配M二E,M是最大匹配当 且仅当G不含M增广路。 ■充分性:采用反证法,假设最大匹配M>M ●和M的对称差的边导出子图的连通分支有什么特征? 2023/4/3 27
n 贝尔热定理:对于图G = <V, E>和匹配M ⊆ E,M是最大匹配当 且仅当G不含M增广路。 n 充分性:采用反证法,假设最大匹配|M’| > |M| l M’和M的对称差的边导出子图的连通分支有什么特征? 2023/4/3 27 匹配和最大匹配
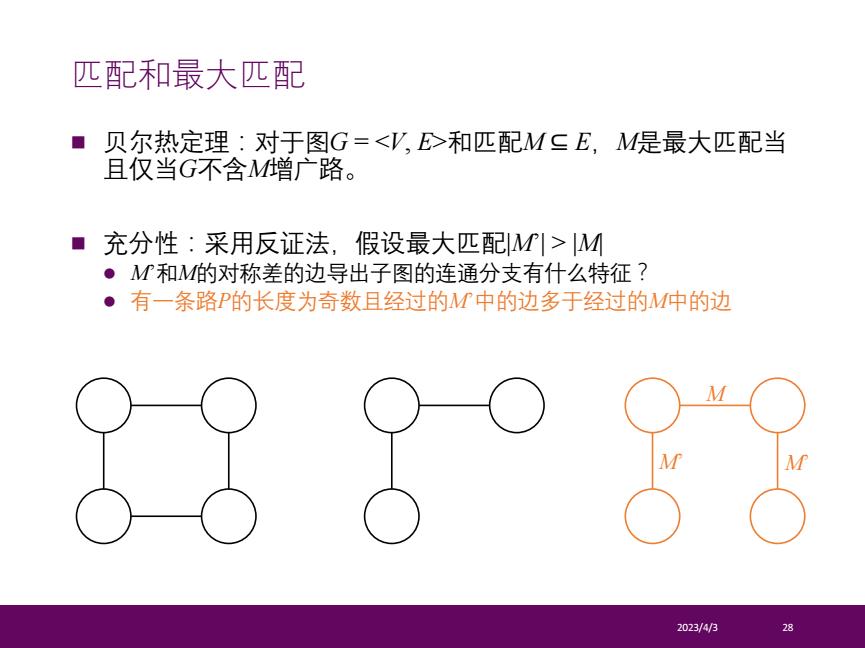
匹配和最大匹配 ■贝尔热定理:对于图G=<V,E>和匹配M二E,M是最大匹配当 且仅当G不含M增广路。 ■充分性:采用反证法,假设最大匹配M1>M ●M和M的对称差的边导出子图的连通分支有什么特征? ●有一条路P的长度为奇数且经过的M中的边多于经过的M中的边 2023/4/3 28
n 贝尔热定理:对于图G = <V, E>和匹配M ⊆ E,M是最大匹配当 且仅当G不含M增广路。 n 充分性:采用反证法,假设最大匹配|M’| > |M| l M’和M的对称差的边导出子图的连通分支有什么特征? l 有一条路P的长度为奇数且经过的M’中的边多于经过的M中的边 2023/4/3 28 匹配和最大匹配 M’ M’ M

匹配和最大匹配 ■贝尔热定理:对于图G=<V,E>和匹配M二E,M是最大匹配当 且仅当G不含M增广路。 ■充分性:采用反证法,假设最大匹配M1>M ●M和M的对称差的边导出子图的连通分支有什么特征? ●有一条路P的长度为奇数且经过的中的边多于经过的M中的边 ●P是M增广路(为什么?),矛盾 2023/4/3 29
n 贝尔热定理:对于图G = <V, E>和匹配M ⊆ E,M是最大匹配当 且仅当G不含M增广路。 n 充分性:采用反证法,假设最大匹配|M’| > |M| l M’和M的对称差的边导出子图的连通分支有什么特征? l 有一条路P的长度为奇数且经过的M’中的边多于经过的M中的边 l P是M增广路(为什么?),矛盾 2023/4/3 29 匹配和最大匹配 M’ M’ M

匹配和最大匹配 ■如何找出图中的最大匹配? 2023/4/3 30
n 如何找出图中的最大匹配? 2023/4/3 30 匹配和最大匹配