
三、原子的质量和体积 ·1、原子的质量 ·可以由原子量和由Avogadro:定律计算 ·Avogadro常数NA:1mol的原子的数量 ·原子量A:1mol的原子的质量 ·一个原子的质量 A M= NA W4=6.022×1023/mol
三、原子的质量和体积 • 1、原子的质量 • 可以由原子量和由Avogadro定律计算 • Avogadro常数NA: 1mol的原子的数量 • 原子量A:1mol的原子的质量 • 一个原子的质量 NA A M = 6.022 10 / mol 23 NA = ×
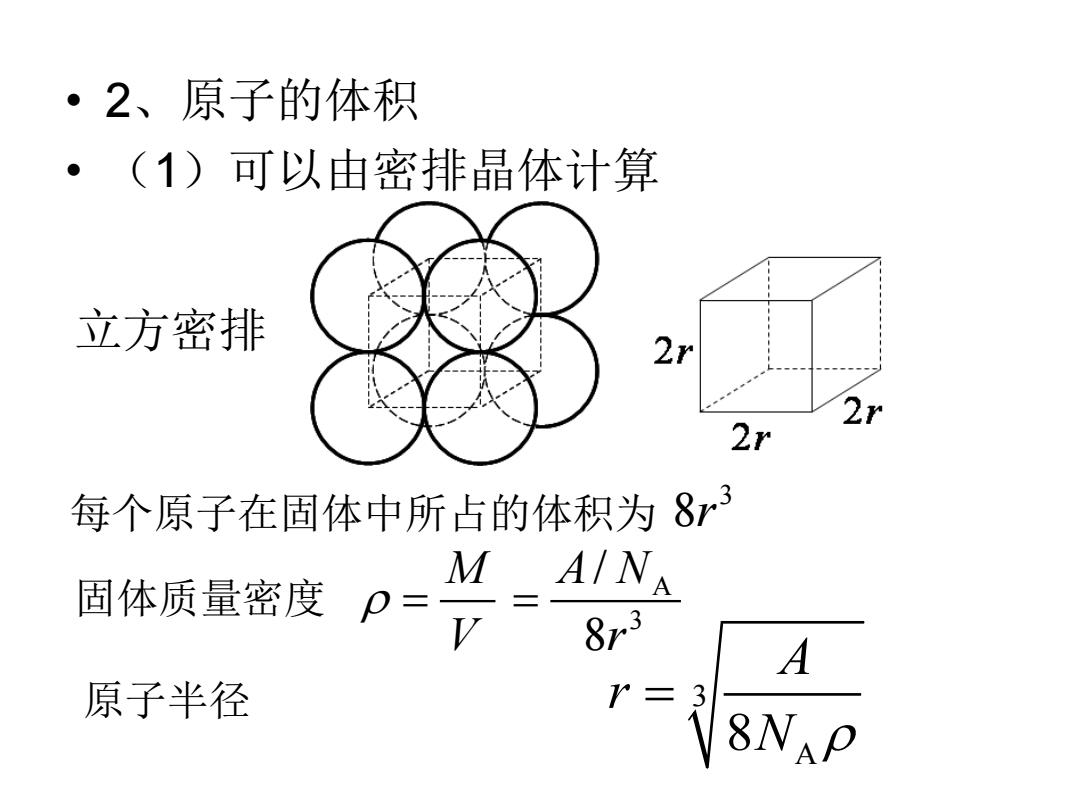
·2、原子的体积 (1)可以由密排晶体计算 立方密排 2r 2r 2r 每个原子在固体中所占的体积为83 M AINA 固体质量密度P= 8r3 A 原子半径 T-iSNAP
• 2、原子的体积 • (1)可以由密排晶体计算 M V ρ = 立方密排 3 每个原子在固体中所占的体积为 8r 3 A 8 A r N ρ = 固体质量密度 原子半径 A 3 / 8 A N r =

六角密排 3 2r 六棱柱的高 22-3-4 2¥ _r 底边长2r 每个原了所占的体积6××2r×V3r 46,16=42r 3 M AIN 质量密度 V 4V2r3 A 原子半径 4PN ~10-10m=1A
六棱柱的高 2 2 底边长 2 46 2 (2 ) ( 3 ) 3 3 rrr − = 2r 每个原子所占的体积 1 46 3 6 2 3 /6 4 2 2 3 ×× × × = rr r r 质量密度 A 3 / 4 2 M A N V r ρ = = ~ 3 4 2 A A r ρN 原子半径 六角密排 10 ~ 10 m 1A − =
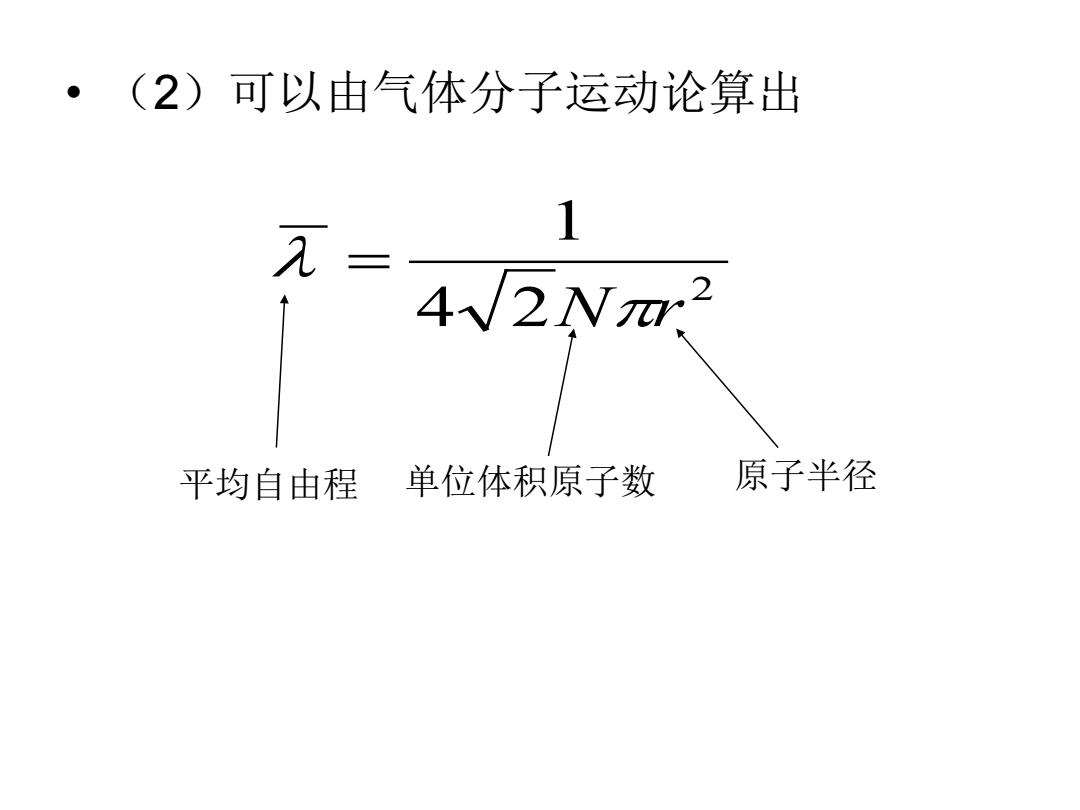
·(2)可以由气体分子运动论算出 1 4√2N2 平均自由程 单位体积原子数 原子半径
• (2)可以由气体分子运动论算出 2 4 2 1 Nπr λ = 平均自由程 单位体积原子数 原子半径

·(3)由von de Waals定律算出 (p+XV-b)=RT ·其中 b=4va Va 原子体积
• (3)由von de Waals定律算出 V b RT V a ( p + )( − ) = • 其中 b = 4Va Va 原子体积