*6-5驻波 驻波的产生 振幅、频率、传播速度都相同的两列相干波,在 同一直线上沿相反方向传播时叠加而形成的一种特殊 的干涉现象, 基频 三次谐频 三次谐频 四次谐频
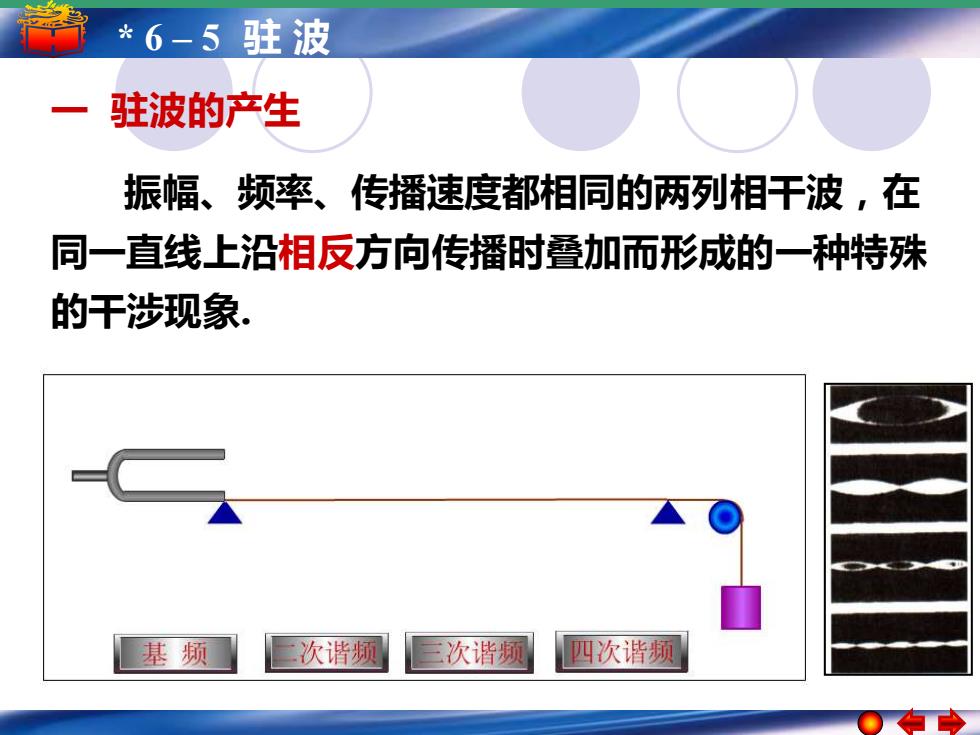
* 6 – 5 驻 波 一 驻波的产生 振幅、频率、传播速度都相同的两列相干波,在 同一直线上沿相反方向传播时叠加而形成的一种特殊 的干涉现象

*6-5驻波 实际观察到的弦上的驻波
* 6 – 5 驻 波 实际观察到的弦上的驻波
*6-5驻波 驻波的形成 t=0 t=1/8T t=1/4T t=3/8T t=1/2T
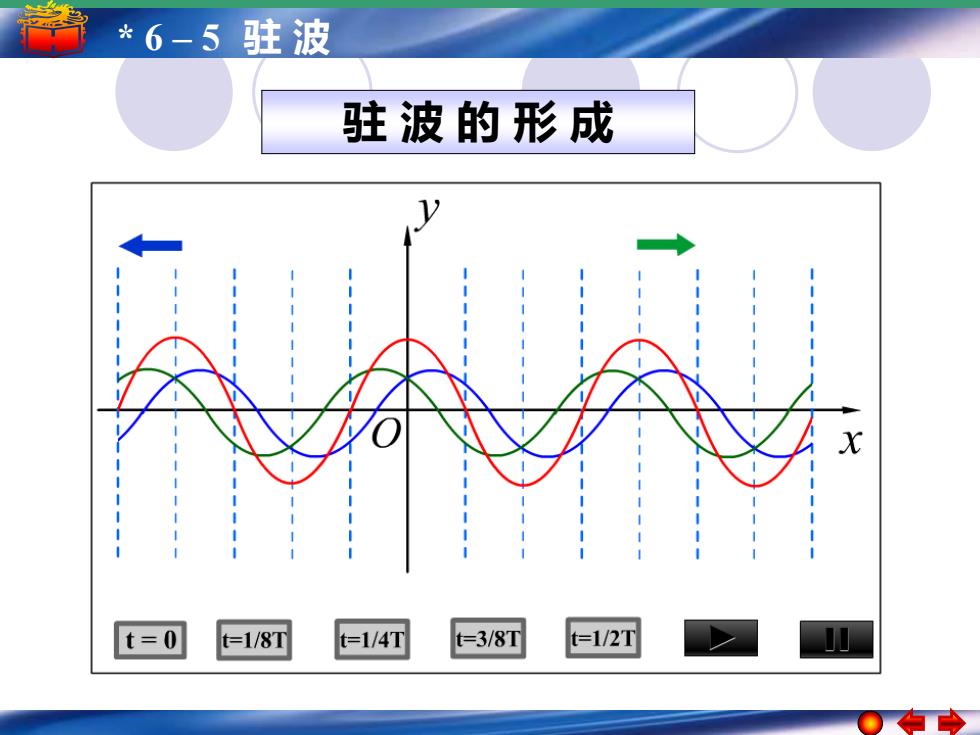
* 6 – 5 驻 波 驻 波 的 形 成

之3 *6-5驻波 二 驻波方程 正向 y1=Acos2元W-分 负向y2=Acos2m(n+) y=y+y2 -Ac0s2r(n-克+Acos2x(t+月》 X 2Ac0S2元 cos2元t 驻波的振幅 各质点都在作同 与位置有关 频率的简谐运动
* 6 – 5 驻 波 驻波的振幅 与位置有关 t x A = 2 cos 2π cos 2π 二 驻波方程 cos 2π ( ) 1 x 正向 y = A t − cos 2π ( ) 2 x 负向 y = A t + 1 2 y = y + y 各质点都在作同 频率的简谐运动 cos 2π ( ) cos 2π ( ) x A t x = A t − + +

*6-5驻波 讨论 驻波方程y=2AcoS2π:c0s2元t (1)振幅 2Acos随X茄异,与时间无关. X=±k元(k=0,1,2,) ±(k+πk=0,12 2 士k (k=0,1)Ax=2A 波腹 、入 (k (k=0,1,.)An=0 波节 相邻波腹(节)间距=九/2 相邻波腹和波节间距=入/4
* 6 – 5 驻 波 t x y A 讨论 ➢ 驻波方程 = 2 cos 2π cos 2π = x cos 2π 2 π = k π (k = 0,1,2,) x ) π ( 0,1,2, ) 2 1 2 π = (k + k = x 1 0 相邻波腹(节)间距 = 2 相邻波腹和波节间距 = 4 (1)振幅 随 x 而异, 与时间无关. x 2Acos 2π 波腹 波节 k (k 0,1, ) A 2A 2 = max = ( 0,1, ) 0 2 ) 2 1 ( k + k = Amin = x =