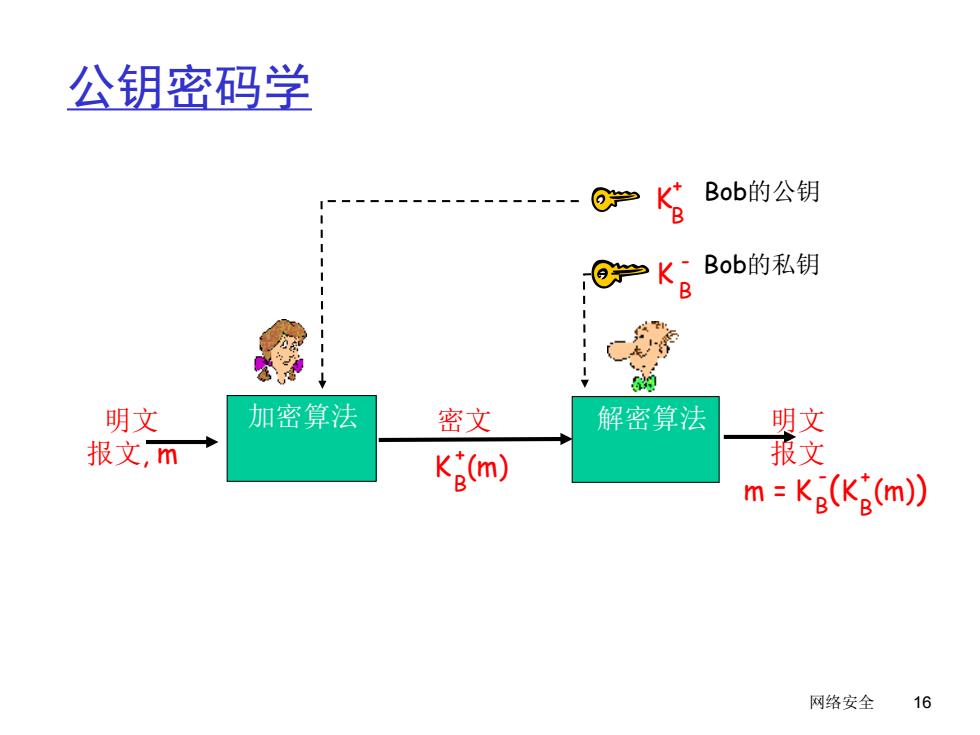
公钥密码学 @学 Bob的公钥 B Bob的私钥 5B 明文 加密算法 密文 解密算法 明文 报文,m Kg(m) 报文 m=K。(Kgm) 网络安全 16
网络安全 16 公钥密码学 明文 报文, m 加密算法 密文 解密算法 Bob的公钥 明文 K (m) 报文 B + K B + K Bob的私钥 B - m = K (K (m)) B + B -

公钥加密算法 要求: 需要K)和K)使得 KeKm》=m 给定公钥K$,不应当能够计算出私 钥KB RSA:Rivest,Shamir,Adelson algorithm 网络安全 17
网络安全 17 公钥加密算法 需要 K ( ) B 和 K ( ) 使得 B . . 给定公钥K , 不应当能够计算出私 钥 K B B 要求: 1 2 RSA: Rivest, Shamir, Adelson algorithm + - K (K (m)) = m B B - + + -

RSA:选择密钥 1.选择两个大的素数p,9.(如每个1024比特) 2.计算n=pq,z=(p-1(q-1) 3.选择e(使e<n)使得与Z没有公因子(e,z是“互素” 4.选择d使得ed-1能够被z整除(换句话说:ed mod z=1) 5.公钥是(n,e).私钥是(n,d) 网络安全 18
网络安全 18 RSA: 选择密钥 1. 选择两个大的素数 p, q. (如 每个1024比特) 2. 计算 n = pq, z = (p-1)(q-1) 3. 选择e (使 e<n) 使得与Z没有公因子 (e, z 是“互素” 4. 选择d 使得 ed-1 能够被z整除(换句话说: ed mod z = 1 ). 5. 公钥是(n,e). 私钥是 (n,d). K B + K B -

RSA:加密,解密 0.给定(n,e)和(n,d)如上面所计算 1.为加密比特模式,m,计算 c=me mod n(即当me被n相除时的余数) 2.为了解密接收到的比特模式,c,计算 m=cdmod n(即当cd被n相除时的余数) 出现魔法! m =(memod n)dmod n C 网络安全 19
网络安全 19 RSA: 加密,解密 0. 给定(n,e)和(n,d)如上面所计算 1. 为加密比特模式, m, 计算 c = m mod n e (即当 me被n相除时的余数) 2. 为了解密接收到的比特模式, c, 计算 m = c mod n d (即当 c d被n相除时的余数) m = (m mod n) e mod n 出现魔法! d c

RSA例子: Bob选择p=5,q=7.则n=35,z=24. e=5(因此e,z互素), d=29(因此ed-1被z整除 (5*29-1)/24=6 字母 m 如e c=memod n 加密: 12 24832 17 解密: S d m=cdmod n 字母 17 481968572106750915091411825223071697 12 网络安全 20
网络安全 20 RSA 例子: Bob选择p=5, q=7. 则n=35, z=24. e=5 (因此 e, z 互素). d=29 (因此ed-1 被z整除 (5*29-1) /24=6 字母 m m e c = m mod n e l 12 24832 17 c m = c mod n d 17 481968572106750915091411825223071697 12 c d 字母 l 加密: 解密: